Wavelet Transform Module for IBM AIX Visualization Data Explorer

Table of Contents

• Introduction
• Goals
• Mathematical backgrounds
• Implementation
  • Color Space Transform
  • Implementation of Wavelet Transform
• Block Diagrams
• Results
• Getting the Modules
• Using the Modules & Examples
• Conclusions
• Acknowledgment
• References

A. Color Space Transform

A color image has separate red, green, and blue (RGB) components. This type of image can not be used when dealing with compression. If an image is to be compressed, RGB formated pixels must be transfer to the formation of grey scale and color differences, known as YUV or YCrCb space. Thus all RGB images must be transfered to YUV color space before forward wavelet transform is performed, and returns to RGB format after inverse wavelet transform. Note that for any image stored in YUV space, human eyes are sensitive to the grayscale images but is not sensitive toward the color difference images. Thus, 4:2:0 color difference coding can be used to further increase the compression ratio [6].

Transform from RGB to YUV:

y =  0.2990 * R + 0.5870 * G + 0.1140 * B

U = -0.1687 * R - 0.3313 * G + 0.5000 * B

V =  0.5000 * R - 0.4187 * G - 0.0813 * B

Transform from YUV to RGB:

R = Y + 0.00000 * U + 1.40200 * V

G = Y - 0.34414 * U - 0.71417 * V

B = Y + 1.77200 * U + 0.00000 * V

B. Implementing Wavelet Transform

The forward and inverse wavelet transforms is implemented using Quadrature Mirror filters (QMF) [7]. The QMF filters consist of a low-pass filter, H, and high-pass filter, G. The relationship between filters H and G is

g(n) = (-1)^n * h(1-n)

Forward wavelet transform is implemented using H_bar and G_bar filters, where inverse wavelet transform is implemented using H and G filters. The relationship between H and H_bar, G and G_bar filters are

g(n) = g_bar(-n)

h(n) = h_bar(-n)

In order to reduce the nonzero wavelet coefficients corresponded to an edge, smaller number of wavelet taps is more desired [7]. Daubechie's 6 taps wavelet "is well known and has some nice properties" [8]. Thus, six taps Daubechie's wavelet is chosen to implement the module. The filter coefficients for Daubechie's six tap wavelet is listed as follow.

h(0) = 0.332670552950

h(1) = 0.806891509311

h(2) = 0.459877502118

h(3) = -0.135011020010

h(4) = -0.085441273882

h(5) =  0.035226291882

A two-dimensional forward wavelet transform can be implemented using 2 one-dimensional forward wavelet transforms; one in horizontal direction, the other in vertical direction.

A one-dimensional data, d is filtered using Daubechie's filter by convolving the filter coefficients h(k) and the input data:

new_d(i) = h(0) * d(i-0) + h(1) * d(i-1) + ... + h(5) * d(i-5)

Please note that the color image is assumed to be periodic; thus circular convolution [9] is used to implement the module.

After filtering the one-dimensional data using Daubechie's filter, downsampling by 2 is followed to reduce the data size to half. See Figures 1 and 2 for detailed forward and inversed wavelet transform block diagrams.

Recall the the relationship between filters g, g_bar, h, and h_bar, coefficients between QMF filters, h_bar and g_bar is differed by 4 delays (see reference [7]). Thus, it is necessary to rotate the image back 4 times during reconstruction.

Block Diagrams

Block diagram for forward wavelet transfrom




Figure 1 illustrates a single forward wavelet transform of a given image. Given an image, f(x,y), it is first filtered along x direction, resulting in a low-pass image, fl(x,y) and a high-pass image fh(x,y). Note that after downsampling by 2, both images have reduced to half on its x direction. Same method is applied on two subimages along y dimension resulting in four subimages : one low-pass, fll, and three high-pass, flh, fhl, and fhh. Hilton, Jawerth, and Sengupta

---

RESULTS

TajSmall.tiff and logo.tiff images are used to test if horizontal, vertical and diagonal features are extracted out from original image into flh, fhl, and fhh subimages. Figure 11 showes the result after one wavelet transform and figure 12 showes the result after three levels of wavelet transform applied to logo.tiff image. Different reconstructed images are shown here to see how higher compression ratio affecting the images. In general, increasing the compression ratio will just reduce the visibility of the edges in the reconstruced images.



Figure 3. TajSmall.tiff, the original RGB color image



Figure 4. The TajSmall image after 4 wavelet transforms. This is the picture after forward wavelet transforms. Four levels of wavelet transforms are applied to the original image.



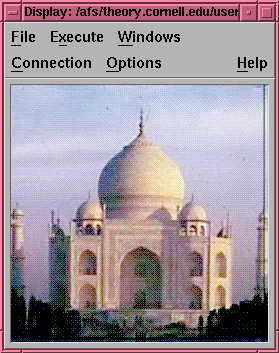
Figure 5. The reconstructed TajSmall image after four levels of wavelet transforms. All high-pass data are stored and used in inverse wavelet transform process.



Figure 6. The reconstructed TajSmall image with 4:1 compression. This image has been compressed using ratio 4:1 by dropping all horizontal, vertical, and diagonal information produced from first level wavelet transform. That is, all the first level high-pass subimages have been assumed to be zero. The result looked almost the same as the original image.



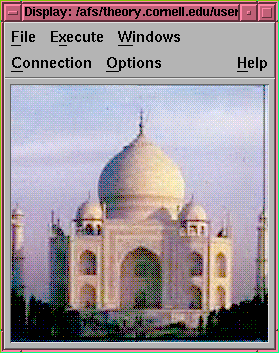
Figure 7. The reconstructed TajSmall image with 16:1 compression. The lossy compression method used here is by dropping all high-pass subimages produced from first and second levels wavelet transform. With higher compression ratio, the reconstruced image starts to loss some edges information. The result still looked very much like the original image.



Figure 8. The reconstructed TajSmall image with 64:1 compression. The lossy compression method used here is by dropping all high-pass subimages produced from three levels of wavelet transform. With 64:1 compression ratio, the final image has lost some of the high-frequency information, resulting in a little blur TajSmall image.



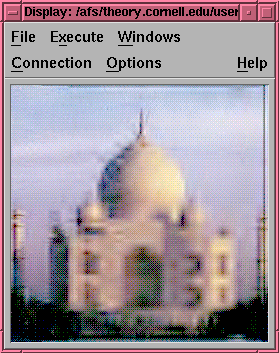
Figure 9. The reconstructed TajSmall image with 256:1 compression. The lossy compression method used here is by dropping all high-pass subimages produced from all four levels of wavelet transforms. With 256:1 compression ratio, the final image has lost lots of edge information, resulting in a very blur TajSmall image.



Figure 10. The original Cornell Theory Center logo image



Figure 11. The RGB logo image after 1 level of wavelet transform. After a single wavelet transform, we can clearly see the horizontal, vertical, and diagonal data has been stored in high-pass subimages.



Figure 12. The RGB logo image after 3 levels of wavelet transforms. After three levels of wavelet transforms, we can see how high-pass data has been extracted out from the average image per each level of wavelet transform.

• Makefile
• wavelet.c
• wavelet.mdf
• userwavelet.c
• TajSmall.tiff
• logo.tiff

---

USING THE MODULE & EXAMPLES

The wavelet transform module takes five inputs from user. Image input must be specified before running the module. If the image is RGB color and in .tiff format, there is no need to enter the width and the height of the image. Otherwise, width and height must be specified. User can enter the number of wavelet transforms to be performed on the image. If no number of level is given, the default value is one level. User should choose whether forward or inverse wavelet transform will be performed in the module; if no input received from user, the default is forward wavelet transform.

For forward wavelet transform, image input must be any RGB color image; the output will be in both YUV and RGB formats. If inverse wavelet transform is used, image input must be in YUV format. Width and height of the YUV image must be given to the module; RGB will be the visible output for observation.



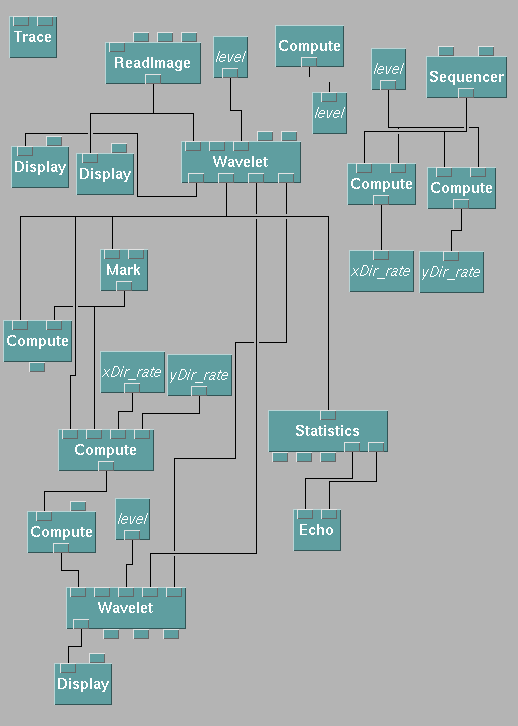
Figure 13. This is how demo.net should look like when displayed in the DX system.