CS 490 Human Motion Simulation

Philip Yen, Spring 1998

Introduction

The goal of this project is to try and simulate human motion with a dynamically realistic model. Essentially, this requires two components, a human model capable of moving like a real human, and an animation model that naturally simulates human motion. This project is implemented using OpenGL for Windows NT/95. The project is written entirely in C, without using MFC for simplicity's sake, instead taking advantage of OpenGL's built in WGL functions for Windows interfacing.

The Model

For familiarization with OpenGL, a simple human model was created with 16 degrees of motion, providing for rotation at the shoulders, elbows, neck, back, hips, knees and ankles (in some cases along multiple axes). Appropriate limb length ratios are observed to make the model appear natural, though the arms seem slightly shorter than normal, due to the lack of hands. In order to better simulate the curvature of the spine, the back is split into two segments, rotated simultaneously. More segments were considered, but they added considerable work later when calculating positions based on joint rotations.

The model is a simple human skeleton built with low resolution cylinders and a 2-D circle for the head, all modelled hierarchically for proper limb movement. Each of the joints is limited to be capable of rotating only within a realistic human range. For example, the neck will only tilt forwards and backwards in a 90 degree range, from -30 degrees to 60 degrees.

This results in a fairly realistic representation of human motion, provided the limits are reasonably set.

The Method

In order to animate the model, some form of inverse kinematics is required, since the destination position and current angles are specified. The algorithm solution provides the angles required to reach the destination. Essentially, we are calculating the angles required, given the destination, as opposed to specifying the angles and calculating the final destination, which is foward kinematic.

The inverse kinematics are solved using a Jacobian matrix based approach. Basically, a Jacobian Matrix relates the changes in angle to the changes in position through the use of partial derivatives, so that the change in a given angle can be calculated from the changes in positions and the inverse of the Jacobian. In cases where the Jacobian is not nonsingular (i.e. square), the pseudo-inverse can be calculated, but, for the sake of simplicity and code reusability, all of the matrices in the code are chosen to be 3x3, limiting the model to 3 joints The process, as taken from the project code, is as follows:

// choose joints to move based on absolute position of cursor

	// set angles from inputs -- convert degrees to radians for trig fcns

	// find position from current angles; 
	// n.b. trigonometric equations formed by hand for each case and hardcoded

	// form jacobian [J] =  [Ja Jb Jc] <= [d(x0)/d(theta1) d(x0)/d(theta2) d(x0)/d(theta3)]
	//			[Jd Jd Jf]    [d(y0)/d(theta1) d(y0)/d(theta2) d(y0)/d(theta3)]
	//			[Jg Jh Ji]    [d(z0)/d(theta1) d(z0)/d(theta2) d(z0)/d(theta3)]
	// n.b. All partial derivatives calculated by hand and hardcoded

	//			  [deltax/n] 
	// find a small delta r = [deltay/n] e.g. a small portion of original difference
	//	        	  [deltaz/n]

	// while still too far away (but within reach of current limbs) calculate jacobian and 
	// solve for inverse of matrix using cramer's rule: ie J-1 = adj(J)/det(J)

	// calculate determinant of [J]
	// n.b. if det = 0, there exists no inverse...

	// inverse of [J] is (1/det)*adj(J)

	// straight matrix multiply, 	[    	][deltax/n]   [dtheta1]  , i.e. dtheta = J*r
	//			 	[   J-  ][deltay/n] = [dtheta2]
	//			 	[	][deltaz/n]   [dtheta3]
	 
	// thus new_theta = theta + dtheta ( a.k.a. +=)

Model Implimentation Details

Not all joints are used in final product, due to target range overlaps. The problem is rooted in the selection of joints in areas which may be accessible to multiple combinations of joints. Since weighting of joints is unreliable, it is more convenient to simply predetermine which joints are to be used in a given target area. Since each of these combinations and their Jacobians must be hardcoded by hand, this limits the number of joints used. As a result we have a smaller, more specialized inverse matrix calculation procedure which is also frequently reused.
The four available "joint packages" are the right/left elbow and shoulder (along the x & y axes) and the right/left shoulder and spine (along the x axis). The right/left limbs each work only on their side of the body, and if the cursor is placed directly in between, neither will respond.
The neck joint keeps the head continously pointed at the cursor. But the calculation is strictly trigonometric, not utilizing the 3x3 Jacobian solution.
The cursor, controlled by the keypad, will be white in color when within reach of any the joint packages. But it will change to red when it strays outside of this target area.
The while loop specified in the code was removed in favor of timer based execution of animation proc with if statements, so the animation can be actually seen. For, even if the screen is refreshed inside the while loop, the procedure does not pass on the update commands until after the while loop has finished, with the resultant appearance of limbs jumping to their destinations.
When new joints are rotated, unused ones incrementally returned to original (unrotated) states. This correction of angle position results in a slight inaccuracy when the joints converge, since the calculations are done with correct values, whereas the real values are +/- 1 degree.
The implementation of back rotation is not robust. There are still occasional lapses where the limbs oscillate, but this is mathematically correct, and more evident during back rotation because of a much larger target area. The simplest solution is to move the cursor into another limb's target range.
Changing the window size will wreak havoc with the cursor movement in the 2-D model. This is because the current corrective values are absolute, instead of based on the relevant variables. But this has been corrected for the simulation model.
There are animated GIF files included below demonstrating each module.

The Product

Initial 2-D Inverse Kinematics Model:
	inverse.exe inverse.c inverse.gif
Initial Human Model:
	model.exe model.c model.gif
Human Motion Simulator:
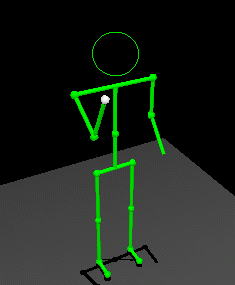	simulator.exe simulator.c simulator.gif

References

Wright, R.; Sweet, M. OpenGL Superbible. Waite Group Press, Corte Madera, CA, 1996
Graham, A. Matrix Theory & Applications for Engineers and Mathematicians. Ellis Horwood Ltd., Publishers, Chichester, UK, 1979
Korein, J.; Badler, N. "Techniques for generating the goal directed motion of articulated structures." IEEE Computer Graphics and Applications, vol.2, no.9, p.71-81.