Central pattern generator/double pendulum model

Bionb 2220, CI Section, 4/27/09

By: Devin Cowan

         

 

Simple spring-mass systems are all around us. Harmonic oscillators have been used to explain everything from the vibration of valence electrons to the “travel” of a bike’s suspension system. This model explores the interaction simple neural networks with dynamical systems whose behavior is based on simple harmonic oscillators. In particular, I used computer simulation to observe the interaction of central pattern generators and the motion of a double pendulum.

 

 

Background:

Central pattern generators (CPG’s) are clusters of interneurons found in both vertebrates and invertebrates (Tytell). These relatively simple neuron networks are capable of synchronizing and producing rhythmic patterns thought to drive repetitive motor movements (Hooper 1). Several studies have demonstrated that oscillatory motor output CPG’s can entrain to an energy efficient frequency of firing when receiving sensory feedback (Iwasaki and Zheng 1). Certainly, it seems that CPG’s will inherently “seek” an energy minimum provided suitable parameters (gain, saturation). However, this has only been demonstrated using single-degree-of-freedom systems; in other words, most studies have modeled the physics of motor output as a simple point-mass pendulum or a spring-mass oscillator (Verdaasdonk, Hatsopoulos).

 

 

Methods:

This study was an attempt to create a more physically realistic model of a CPG/limb system. The primary difference between this and previous work is the use of a double pendulum (Figure 1) rather than the “limbs” mentioned above.

 

 

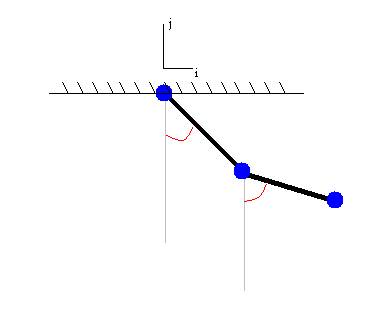
Figure 1: Double pendulum, 2-DOF

 

 

 

Using this novel model, I wanted to observe the limb behavior for different parameter settings and initial conditions. I thought that some interesting patterns, like those in other 2-DOF systems, might arise. Figure 2 shows one such pattern—the displacements of two masses as they are forced near one of the system’s eigenvalues (a normal mode frequency).

 

 

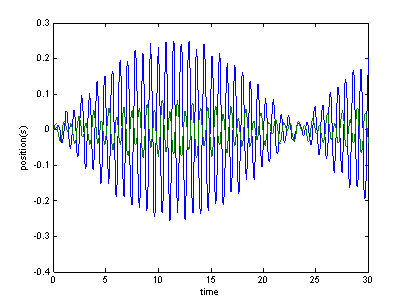
Figure 2: Oscillations of a 2DOF system that is forced near its natural frequency

 

 

 

In addition to introducing a second degree of freedom, the double pendulum system necessitated the use of two central pattern generators—one driving each set of flexor and extensor muscles (each joint, “elbow” and “shoulder” had one such set of muscles). Figure 3 is a connection diagram for the model, modified from Iwasaki and Zheng.

 

 

 

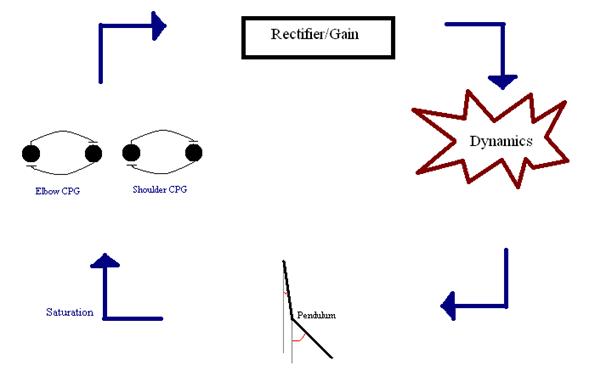
Figure 3: Flow diagram for model system—two CPG’s and a double pendulum

 

 

 

 

The CPG’s were both modeled using Izhikevich’s numerical integrator. Each consisted of two reciprocally inhibiting neurons, whose output was rectified (to account muscle contraction, as opposed to active extension) and amplified before driving the motion of the pendulum.

 

A great portion of my efforts were spent on determining the equations of motion for the double pendulum, and implementing them in such a way that they could be numerically integrated within Izhikevich’s construct (which uses a Euler’s Method type integrator). The equations were determined using angular momentum balance about hinge points. Inertial terms were not neglected. A damping moment, proportional to the angular velocity of the limb segment, was accounted for at the “elbow” and “shoulder” joints. Neural output from the CPG’s was implemented as a direct moment about each of the joints. For further details, follow Ruina and Pratap’s similar example of a robotic arm (930).

 

Because the dynamics of the physical model are complex, this model was tested in standalone before addition of the CPG’s. Figure 4 shows one such test, in which the double pendulum was released with no initial velocity. As expected of a damped oscillator (note that both joints were damped), the system’s motion eventually ceases.

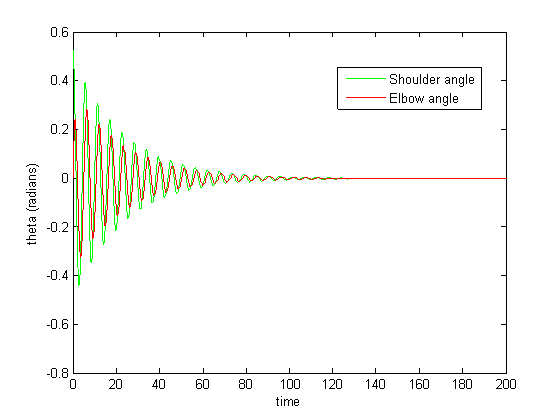
Figure 4: Motion of a double pendulum agitated at t=0, without neural interaction

 

 

 

Similarly, the behavior of the CPG neurons before addition of sensory feedback was recorded (Figure 5).

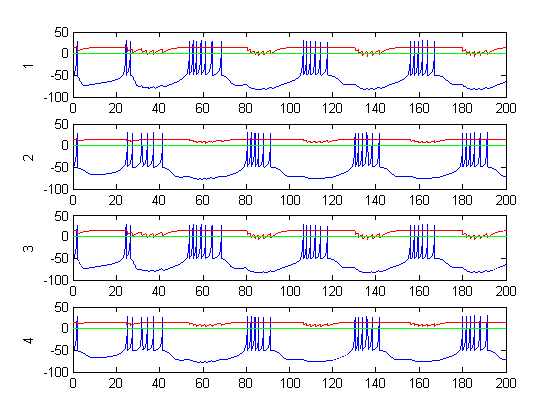
Figure 5: Behavior of CPG’s without feedback from the pendulum

 

 

 

Results:

With a baseline set of data in hand, I enabled driving and feedback in the CPGs. Using parameters from Iwasaki and Zheng, the CPG/pendulum system was scaled up to its full connectivity. Below are several of the outputs:

 

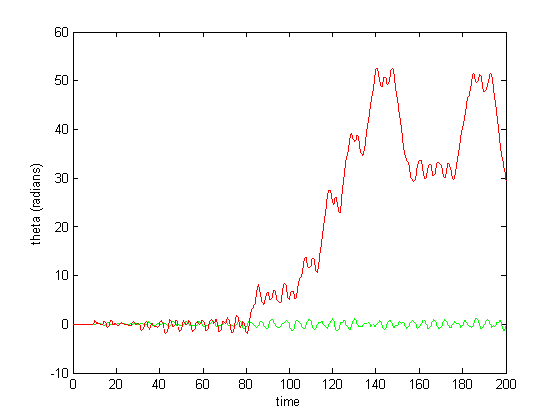
Figure 6: Rod positions during CPG activity (dt=.01, tend=200, gain=1)

 

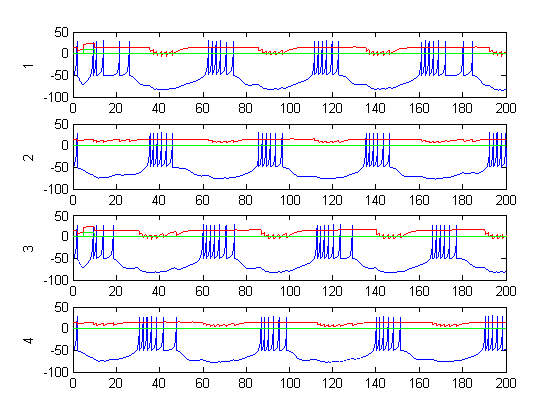
Figure 7: CPG activity with feedback

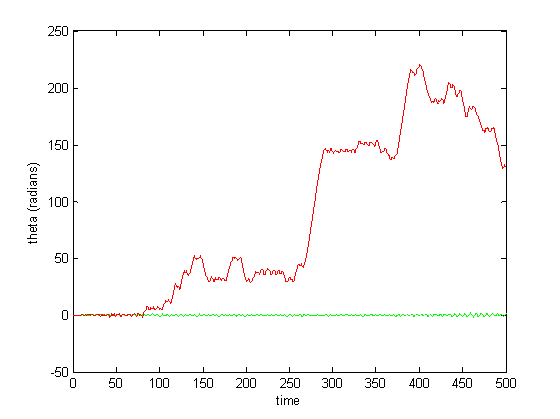
Figure 8: positions during CPG activity (dt=.01, tend=500, gain=1)

 

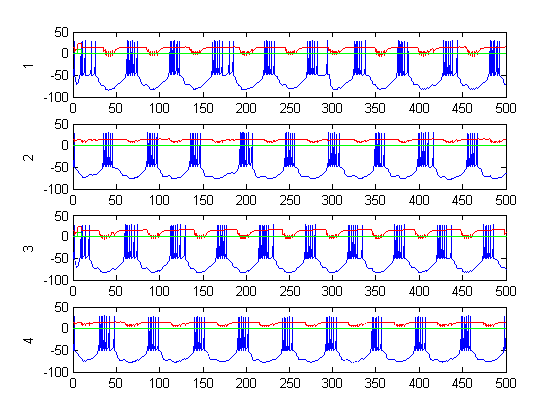
Figure 9: CPG activity with feedback (over a long period)

 

 

 

Figure 6-8 show incredibly huge (not to mention physically impossible) position values for the two rods of the double pendulum. I quickly found that this could be remedied by decreasing the gain (Iwasaki and Zheng witnessed entrainment for gain~1). However, the decreased gain resulted in still other problems—radical shift patterns like that of Figure10 were observed at low gain values.

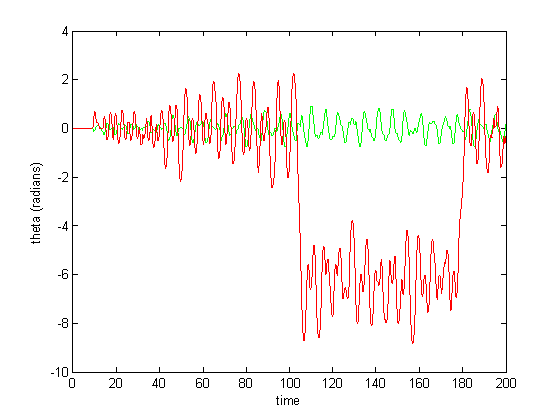
Figure 10: Radical shifting pattern of mothion

 

 

The abrupt spiking in Figure 10 diminished upon integration with a smaller step size.

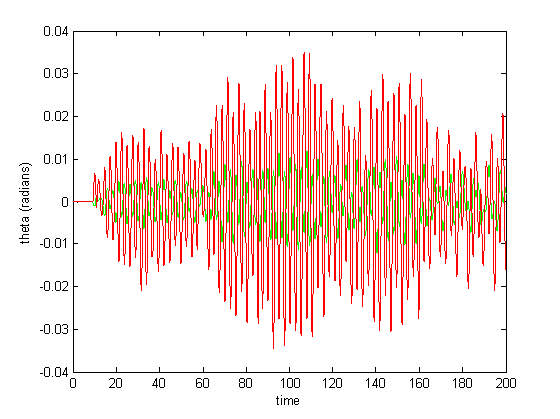
Figure 11: Small step size integration

 

Discussion:

Despite that the results in Figure 11 closely resemble the motions of a near-harmonic 2-DOF system (Figure 2), replication of other such patterns (and verification that they aren’t simply artifacts of the parameters and integration times) was hindered by several constraints:

 

Despite that my goal of searching for oscillatory limb patterns was obviated by my choice of computer model (and its computational demand), I feel that this project has other contributions. I hope that my painstaking double-pendulum implementation might prove useful in other models, if in no other way than by raising the standard of modeling from “spherical chickens” to spherical chickens that have joints!

 

 

References:

 

Hatsopoulos, Nicholas G. Coupling the Neural and Physical Dynamics, Neural Computation 1996, 8, 567-581.

 

Hooper, Scott L. Central Pattern Generators. Embryonic ELS 1999, 1-12.

 

Iwasaki and Zheng. Sensory feedback mechanism underlying entrainment of central pattern generator to mechanical resonance, Bio. Cybernetics 2006, 94:245-261.

 

Izhikevich, Eugene. Simple Model of Spiking Neurons, IEEE Transactions on Neural Networks (2003) 14:1569- 1572 (electronic resource: <http://vesicle.nsi.edu/users/izhikevich/publications/spikes.htm>).

 

Ruina, Andy and Pratap, Rudra. Introduction to Statics and Dynamics. Pre-release version for Oxford University Press: 2008.

 

Tytell, Eric. The Benefits of Positive Feedback, Journal of Experimental Biology 2007, iv.

 

Verdaasdonk, B.W. Energy efficient and robust rhythmic limb movement by central pattern generators, Neural Networks 2006, 19: 388-400.

 

 

Code:

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% Neural Network Simulator

% Using models from Izhikevich

% http://nsi.edu/users/izhikevich/publications/spikes.htm

% Bruce Land -- BioNB 222, March 2008

% Additional edits by Devin Cowan April 2009

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function izRob()

clf

clear all

clc

% Number of neurons

nNeuron = 4 ;

% Number of Sensory cells

% In this version they must be equal

nSense = nNeuron;

 

%timing

dt = .01; %time step

tEnd = 200; %maximum simulation time

%build the time vector

time = 0:dt:tEnd ;

 

%CPG and dynamics parameters

q=.4; lam=2; %Used for saturation feedback function

sDamp=10; %Damping coefficient in the shoulder

eDamp=10; %Damping in the elbow

l1=4; l2=3; %Half length of the upper and lower leg

l3=2*l1; %The com is centered on the first section

m1=30; m2=15; %Mass of limb segments

g=9.8; %Gravitational constant

ihat=[1;0;0]; jhat=[0;1;0]; khat=[0;0;1]; %Frame basis vectors

I1=1/12*m1*(l1*2)^2; %Moment of inertia

I2=1/12*m2*(l2*2)^2;

 

%cell parameters from Izhikevich web page. See:

% http://nsi.edu/users/izhikevich/publications/spikes.htm

%   a           b       c       d       current

pars=[0.02      0.2     -65      6      14 ;...    % tonic spiking

    0.02      0.25    -65      6       0.5 ;...   % phasic spiking

    0.02      0.2     -50      2       15 ;...    % tonic bursting

    0.02      0.25    -55     0.05     0.6 ;...   % phasic bursting

    0.02      0.2     -55     4        10 ;...    % mixed mode

    0.01      0.2     -65     8        30 ;...    % spike frequency adaptation

    0.02      -0.1    -55     6        0  ;...    % Class 1

    0.2       0.26    -65     0        0  ;...    % Class 2

    0.02      0.2     -65     6        7  ;...    % spike latency

    0.05      0.26    -60     0        0  ;...    % subthreshold oscillations

    0.1       0.26    -60     -1       0  ;...    % resonator

    0.02      -0.1    -55     6        0  ;...    % integrator

    0.03      0.25    -60     4        0;...      % rebound spike

    0.03      0.25    -52     0        0;...      % rebound burst

    0.03      0.25    -60     4        0  ;...    % threshold variability

    1         1.5     -60     0      -65  ;...    % bistability

    1       0.2     -60     -21      0  ;...    % DAP

    0.02      1       -55     4        0  ;...    % accomodation

    -0.02      -1      -60     8        80 ;...    % inhibition-induced spiking

    -0.026     -1      -45     0        80];       % inhibition-induced bursting

 

%extract the cell type for each neuron

nType = [3 3 3 3] ;

a=pars(nType,1)';

b=pars(nType,2)';

c=pars(nType,3)';

d=pars(nType,4)';

Is = pars(nType,5)'; %steady current

 

%synaptic connections

%The weight matrix -- (+)excitatory: (-)inhibitory

SynStrength =10*[0 -.5 0 0;

                 -1 0 0 0;

                 0 0 0 -.5;

                 0 0 -1 0] ;

 

%each neuron also potentially has several sensory inputs

SenseStrength =[1 0 0 0;

                0 1 0 0;

                0 0 1 0;

                0 0 0 1];

 

%Sense inputs are time vectors on the inputs--DIRECT INPUTS from experiment

SenseInput(:,1) = 10* (time>5 & time<10);

SenseInput(:,2) = 0 * (time>5 & time<10);

SenseInput(:,3) = 10 * (time>5 & time<10);

SenseInput(:,4) = 0 * (time>5 & time<10);

 

%synaptic current rises instantly, then decays exponentially

%set the decay rate of synaptic current to about 3 mSec

SynRate = .3*ones(1,nNeuron);

SynDecay = 1 - SynRate*dt;

 

%init state variables

v = c; % reset voltage;

s = zeros(1,nNeuron); % spike occurance

u = zeros(1,nNeuron); % revocery variable

 

%initial input currents

Istate = 0;  %state variable used for synaptic currents decay

I = Is ;

 

%step the time

tindex = 1; %pointer for output arrays

 

%init plotting variables

Vout = zeros(length(time),nNeuron);

Aout = zeros(length(time),nNeuron);

THout=zeros(length(time),6); %1&2 are theta vals, 3&4 are thetadot vals

 

th=zeros(1,6);%Initialize theta values...0=leg starts downward

M=[0 0;0 0]; %Dynamics matrix used for calc of ang. accelerations

RHS=[0;0];

 

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%MAIN LOOP

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

for t=time

    %add values to plotting variables

    Vout(tindex,:)=v;

    Iout(tindex,:)=I;

    THout(tindex,:)=th;

   

   

    %DO DYNAMICS--assign vals to th

    ms=detMoment(v(1:2)); %Find the moments based on the v's

    me=detMoment(v(3:4));

   

    tTemp=th(1:2); tdTemp=th(3:4); tddTemp=th(5:6); %Unpack vars

   

    %Differential equations

    th(1:2)=tTemp+dt*tdTemp;

    th(3:4)=tdTemp+dt*tddTemp;

   

    %Angular momentum ballance to calc. angular accelerations

    lam1=sin(tTemp(1))*ihat-cos(tTemp(1))*jhat; %Unit vercots along the two sections

    lam2=sin(tTemp(2))*ihat-cos(tTemp(2))*jhat;

    %Define various physical parameters

    rg1o=l1*lam1; rg2e=l2*lam2; reo=l3*lam1; rg2o=reo+rg2e;

    sumMe=cross(rg2e,-m2*g*jhat)+me*khat-eDamp*tdTemp(2)*khat; %RHS of AMB

    sumMs=cross(rg1o,-m1*g*jhat)+cross(rg2o,-m2*g*jhat)...

        +ms*khat-sDamp*tdTemp(1)*khat; %Damping prop. to angular velocity

    T1=cross(khat,reo); T2=cross(khat,rg2e); T3=tdTemp(1)^2*reo+tdTemp(2)^2*rg2e;

    M(1,1)=dot(m2*cross(rg2e,T1),khat);

    M(1,2)=dot(m2*cross(rg2e,T2)+I2*khat,khat);

    addE=m2*cross(rg2e,T3);

    RHS(1,1)=dot(sumMe+addE,khat);

    T4=-tdTemp(1)^2*rg1o; T5=cross(khat,rg1o);

    M(2,1)=dot(m1*cross(rg1o,T5)+I1*khat+m2*cross(rg2o,T1),khat);

    M(2,2)=dot(m2*cross(rg2o,T2)+I2*khat,khat);

    addS=-(m1*cross(rg1o,T4)-m2*cross(rg2o,T3));

    RHS(2,1)=dot(sumMs+addS,khat);

    th(5:6)=inv(M)*RHS; %Invert M to calculate the angular accelerations

   

   

    %input current to cells

    %decaying synaptic currents

    Istate =  s*SynStrength + Istate .* SynDecay ;

   

    %Sensory inputs (direct and from muscle mechanoreceptors)=saturation(th)

    saturation=q*tanh(lam*th(1:2)); %Two sat vals, one for each limb seg.

    sat=[saturation(1) -saturation(1) saturation(2) -saturation(2)]; %All neurons are driven directly by mechano.

    SenseInput(tindex,:)=SenseInput(tindex,:)+ sat;

    I = Istate +  Is + SenseInput(tindex,:)*SenseStrength;

 

    %update state variables

    v = v + dt *(0.04*v.^2+5*v+140-u+I); %Neural ODE's

    u = u + dt * a .* (b.*v-u);

   

    s = zeros(1,nNeuron) ;

    fired=find(v>=30); % indices of cells that spiked

    if ~isempty(fired)

        v(fired) = c(fired) ;

        u(fired) = u(fired)+d(fired) ;

        s(fired) = 1 ; %used in the next time step for synaptic input

    end;

  

    %update time index

    tindex = tindex+1;

 

end %main time step for-loop

 

%Plot the CPG activity

figure(1)

clf

np=nNeuron ;

for i=1:nNeuron %Plot the currents and voltages of the neurons

    subplot(np,1,i)

    plot(time,Vout(:,i))

    hold on

    plot(time,Iout(:,i),'r')

    plot(time, SenseInput(:,i)*SenseStrength(i,:), 'g')

    ylabel(num2str(i))

    set(gca,'ylim', [-100 50])

end %Neuron plotter

 

%Plot the position over time

figure(2)

plot(time,THout(:,1),'g',time,THout(:,2),'r')

xlabel('time'); ylabel('theta (radians)')

 

%Call the animation function

leg(THout(:,1),THout(:,2),time,2*l1,2*l2) %Animate a leg

end %of iz

 

function leg(th1,th2,time,l1,l2)

%Takes post-integration theta values and animates them

for i=1:length(time);

e=l1*[sin(th1(i)); -cos(th1(i))];

h=e+l2*[sin(th2(i)); -cos(th2(i))];

 

upper=[[0;0] e];

lower=[e h];

 

x1=upper(1,:);

y1=upper(2,:);

 

x2=lower(1,:);

y2=lower(2,:);

 

figure(3)

pause(time(2)-time(1))

plot(x1,y1,x2,y2)

axis('equal');

axis([-10 10 -20 5]);

end

end

 

function M=detMoment(v)

%Determines the moment to apply, given the two voltages of the CPG

gain=1;

M=gain*(max(v(1),0)-max(v(2),0));%neuron 1 applies as positive moment

end %Of detMoment