Measuring the "Complexity" of a time series
Bruce Land and Damian Elias
Introduction
People want to measure the complexity
of various signals, such as bird song, ECG, a protein sequence or DNA. For instance,
for ECG, there is the observation that healthy hearts seem to have a more varied
and complex beat rate. Measuring the complexity of a ECG signal might be used
as a diagnostic tool. Complexity estimates have been perfromed on DNA (Gusev,et.al.
1999, Orlov)
(review by Potapov,
et.al.), evolutionary sequences (Adami 2003), morphology (Fusco and Minelli
2000), development (Ricardo, et.al. 2005), maunfacturing (Efstathiou,
et.al.), information systems vulnerability analysis (Bush
and Hughes 2003), well as on various time series outlined below. There are
many proposed measures of complexity and very little agreement about their usefulness
or rigor (e.g. Perakh, or Crutchfield 2000, or Shalizi
2003, or Masum
1995 or Jäntti
2004)The variety of measures is bewildering and daunting, however I will
attempt to classify and outline what little I understand so far. Funes
has a readable summary of the field.
Techniques Review
We are going to consider only time series analysis in this section. There are
reviews of "complexity measures" (Feldman
and Crutchfield 1998, Daw,
et.al. 2002). Kuusela, et.al. (2002) compare the results of ten different
complexity measures on heart rate and blood pressure time series.
- Information theory estimates of complexity
In general the entropy of a discrete probability distribution is given
by
H = sumi(-pi*log(pi))
where i indicates one of the discrete states and sumi
means to sum over all the discrete states. The entropy is larger if each discrete
state has about the same probability of occurence. If you use a base-2 log,
then the entropy represents the number of bits of information which can sent
by a signal consisting of one state. As an example, if you have 4 possible
states of a signal, all with equal probability, then the entropy is
H = -4*(1/4*log2(1/4)) = -4*(1/4*(-2)) = 2 bits. So sending
one of the states (perhaps the one of letters A-D) would transmit 2 bits of
information. Sleigh
et.al. compare five measures of entropy used to classify EEG.
- Approximate Entropy
Pincus (1991) introduced Approximate Entropy as a complexity measure.
Given groups of N points in a series, the approximate entropy is related
to the probabilty that two sequences which are similar for N points remain
similar at the next point. He used this technique to characterize three
chaotic systems.
- EEG
Rezek
and Roberts (1998) compare Fourier entropy (see below) and approximate
entropy and conclude that they both can distunguish anesthesia depth
(as judged by agent concentration). Deeper anesthesia means lower
complexity. Approximate entropy may have been slightly more sensitive
to changes than Fourier entropy. Bhattacharya (2000) used approximate
entropy to characterize the EEG of pathological groups compared with
healthy groups. The degree of linear complexity is significantly reduced
for the in the seizure group for most of the electrodes, whereas a
distinct discrimination between the maniac and healthy
groups based on these nonlinear measures was not evident.
- Respiration
Burioka et.al. (2003) used approximate entropy to measure the complexity
of EEG and respiratory motion diring different stages of sleep. They
found that the entropy of the two signals was related and both decreased
during deep sleep.
- Sample entropy
A modification of the Approximate Entropy introduced by Richman and Moorman
(2000). They claim that approximate entropy as defined by Pincus is biased
by including self-matchs. They also simplify the calculation somewhat.
There is a matlab function available
to compute the sample
entropy. Authors are DK Lake (dlake@virginia.edu), JR Moorman and
Cao Hanqing.
- Neonatal heart
Lake et.al. (2002) use sample entropy to predict neonatal sepsis from
heart rate data. They suggest ways to evaluate the optimal setting
for the parameters (length of sequence, error tolerance) used in sample
entropy. They found that sepsis could be predicted by the sample entropy,
but that much of the difference was related to spike-like outliers
in the data.
- Fourier entropy
To compute the Fourier entropy, a power-spectral-density of a time series
(or portion thereof) is computed. The PSD is normalized to produce a probability-like
distribution, and the entropy calculated as shown above. Fourier entropy
seems to be the baseline against which other methods are shown to be better,
but quite often is the easiest compute if the data sets are large.
- Wavelet entropy
Rosso et.al. (2003) use wavelet transforms (as well as other measures)
to characterize seizure states from EEG recordings. Jones et.al. (2002)
used a 2D wavelet transform of 2D recordings of head surface potentials.
The complexity measure was related to the number of wavelet components
needed to fit the signal.
- Renyi Entropy (Gonzalez, et.al. 2000)
This scheme computes the time-frequency spectrogram of a signal, then
counts the connected regions above some threshold energy. The idea here
is that one peak in time-frequency space is an elementary event, so counting
peaks gives an estimate of complexity. There are tools for time-frequency
analysis available from François Auger, Patrick Flandrin, Olivier
Lemoine, and Paulo Gonçalvès.
- Higher Order methods. (Gu, et.al. 2004)
Break the time series into parts, compute the entropy of each part using
your favorite method, then treat the entropy values as a time series and
compute the entropy of that sequence. Gu, et.al. used this to study EEG
and a couple of chaotic systems using Approximate Entropy (see above)
as the entropy measure. They have a good discussion about periodicity,
randomness and complexity.
- Multiscale/Multiresolution methods
Any of the above entropy measures can be adapted to consider different
time-scales of of the time series. To me, using a multiscale approach
is essential to avoid artifacts of oversampling and noise and because
different structures may emerge from a time series when observed at different
time scales. The most basic way is to analyse the signal at different
bandwidths, or equivalently by averaging together groups of points. Torres
and Gamero (2000) using sliding windows of varying width to estimate a
sort of "instantaneous complexity". Costa et.al. (2002) downsample
the time-series using a rectangular window which they move along the series
in jumps equal to the window width. They calibrate the method with 1/f
noise and white noise. They found that multiscale methods could distinguish
healthly, congestive heart failure, and atrial fibrillation subjects.
There is also a tutorial
and software online. Costa et.al. (2003) have also used multiscale
methods to study normal human gait and used shuffled data as a control.
Costa et.al. (2005) explain multiscale techniques well and apply them
to heart rate and DNA sequences.
- Chaos-based estimates of complexity
- Lyapunov exponent
Efstathiou,
et.al. compare entropy-based complexity measures with Lyapunov exponent
estimates. They conjecture that the Lyapunov exponent measures the rate
at which the system generates new information.
- permutation entropy
Bandt and Pompe (2002) introduced a complexity measure which has aspects
of both dyna mical systems and entropy measures. They propose to estimate
complexity as the entropy of the distribution of permutations of groups
of time samples. Take each member of the group and give it a sequence
number (in the series) from 1 to n. Reorder the n members of each group
into assending order and note the new order of the sequence numbers for
each group. The new order serves as a bin number into which the total
count of all groups with a given sequence is accumulated. The result is
a histogram of number occurances of each sequence order. Normalize this
to a probability distribution and compute the entropy. The authors used
the method on model systems such as the logistic equation.
- Komologrov estimates (algorithmic complexity)
- Lempel-Ziv (Ziv and Lempel 1978, Evans, et.al. 2002)
The time series is first reduced to a symbol list. Some authors set any
voltage (or other measurement) above the mean to one and below the mean
to zero. The string of symbols (often a pattern of 1/0s) is then scanned
for repeated sequences of all lengths. Amazingly, this can be done in
a single pass and is quite efficient. The measure of complexity is then
related to the length of the original sequence and the (generally shorter)
length of the description when repeated sequences are correctly noted
and enumerated. This sceme is also the basis for compression of TIFF images
and ZIP files, where it is refered to as LZW compression (Lempel-Ziv-Welch).
Khalatur et.al. (2003) have actually used the UNIX utility GZIP compression
ratio as a measure of complexity. See also Potapov,
et.al. for web accessable tools. An optimized variant of compression-based
complexity measure is described by Evans
and Bush, 2002. Radhakrishnan et.al. (2000) propose an improved partitioning
method of a continuous signal into symbols for LZ processing.The methoditeratively
finds optimum amplitude clusters in the original signal. Rapp, et.al.
(2001) show how to normalize LZ complexity measures to account for varying
sample lengths and sampling frequencies.
- Spike trains
Szczepanski, et.al.(2003) used LZ complexity to classify spike trains
from ferret visual cortex. They used two methods to encode the train
into symbols (e.g. binning or interspike interval) and showed that
different codings produced different estimated complexities. Also,
in vivo preps yielded higher complexities (carried more Shannon
information) than in vitro preps.The same group (Amigo, et.al.
2004) uses the LZ complexity to estimate the entropy of spike trains.
They found better convergence rates for estimates on short data sequences.
- DNA
Many DNA studies are reviewed in
Potapov et.al. and Orlov
et.al. Complexity meaures may be able to distinguish coding from
noncoding regions. They may be able to distinguish mutational mechanisms.
They can distunguish repetitive regions. Allison
et.al. (1998) suggest a scheme for using approximate string repeats,
rather than exact matches and apply it DNA sequences. They also have
sone online
tools for DNA analysis.
- EEG
Watanabe, et.al. (2003) showed that LZ complexity was sensitive to
the state (eyes open/closed) of subjects. The EEG signals were converted
to symbol sets by binary threshold at the median voltage.
- Depth of Anaesthesia
Hunag et.al. (2003) used LZ complexity as an indicator of changes
in the brain during anathesia. The complexity values were used as
inputs to a neural net classifier.
- Hidden Markov
Shalizi, Et.al. (2001 and 2002)
are not actually concerned with complexity measures (In fact they dismiss
them, Shalizi
2003,), but rather with estimating the minimal set of Markov states
which can statistically reproduce the behavior of a data set. Other people
(e.g. Gunther 1994) have related markov desciptions to complexity measures.
- State machine
- Bird song (Sasahara and Ikegami 2004)
The birds are modeled as finite state-machines which are allowed
to evolve. Complexity is measured as the ratio of total number of
states to the total number of arrows connecting states. This is sort
of an average index of branching in the song. Note that this paper
was a modeling paper, with no attempt to fit state-machines to real
songs.
Our Attempts
We are interested in comparing communications signals between species, modalities,
genera, etc. We tried a few different schemes to see if we could come up with
a useful measure.
We found Matlab code to compute sample entropy. Test
cases for sines, noise and a simple chaotic system (logistic
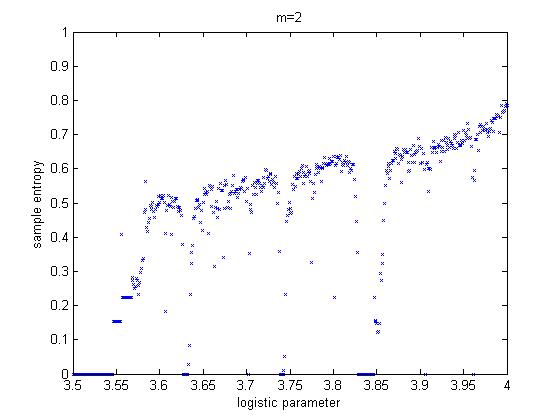
equation) were written. The figure below shows output for the logistic equation
over a range of growth values, for sample length m=2.
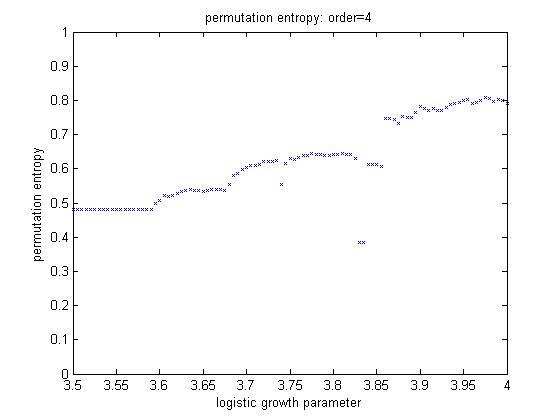
We also wrote code to compute permutation entropy.
The test case used was, again, the logistic equation. The program plots the
computed entropy versus the logistic growth rate, which is periodic for some
regions and chaotic for others. The figure below shows output for 4th order.
You can clearly see some regions of stability around 3.83.
Neither sample entropy or permutation entropy worked very well for the long
data sets we are interested in analyzing, but we had not read about (nor yet
figured out ourselves) the multiscale approachs mentioned above. We need to
redo the sequences with multiscale techniques (for example, Costa et.al. 2003).
We developed a simple technique which is multiscale and which has given interesting
results, but which suffers from all of the defects noted in various reviews
of complexity measures: The technique is without relation to any other measure,
it is not supported by theory, and has few physically interpretable parameters.
A description of the algorithm follows. A signal is divided into N non-overlapping
segments. For each segment, the Fourier entropy is calculated, then the mean
and standard deviation of all N entropies are computed. The measure of entropy
(at the time scale N) is the product of the mean and standard deviation. The
measure is recomputed for a large range of Ns, to account for structuring on
different scales. The measure tends to zero for sine waves and white noise.
It indicates a higher "complexity" for many sorts of non-stationary
signals. For example AM or FM modulation appears as higher complexity compared
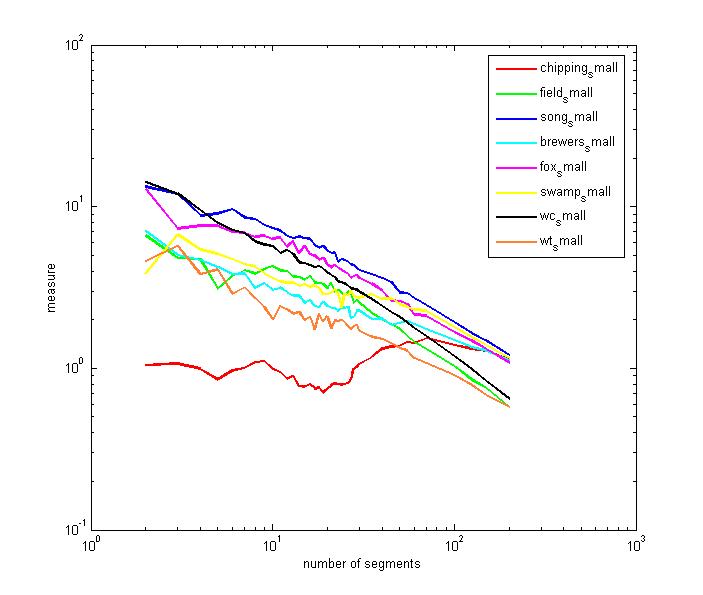
to noise or sine waves. A bird song example is shown below. Eight species of
sparrow were characterized. Single repeats of the entire song were isolated
(by Damian) and analysed. The spectrograms are here.
The "complexity" ordering from the plot roughly matches the ordering
of the spectrograms (as done by Damian, no double blind). The ordering was (from
most complex to least) song, fox, swamp, field, white crown, brewers, white
throat,chipping.
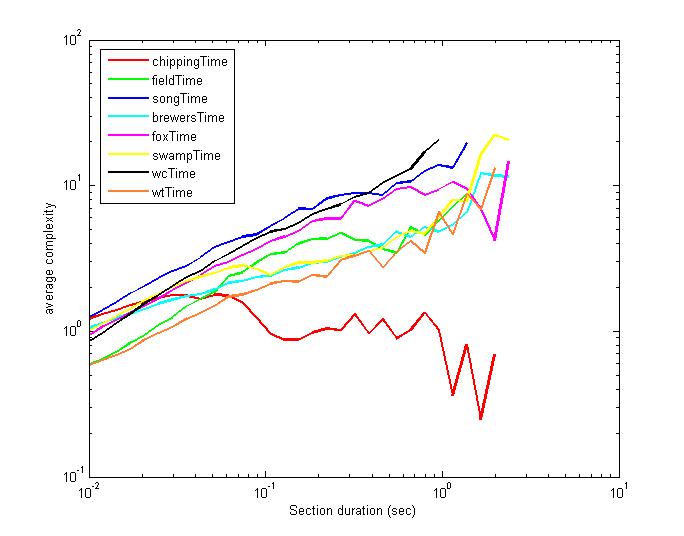
We redid the analysis using fixed length segments instead of N/song, as was
done above. The ordering of the songs changes somewhat.
The next two things to try are the second order entropy techniques and the
Renyi entropy.
References
- Adami, CI, Sequence Complexity in Darwinian Evolution, Complexity
(2003) (pdf)
- Allison L, T. Edgoose, T. I. Dix, Compression
of Strings with Approximate Repeats, Intelligent Systems in Molecular
Biology (ISMB98) pp8-16, Montreal, 28 June - 1 July 1998
- Amigó J. M., Szczepaski J., Wajnryb E., Sanchez-V. MV, Estimating
The Entropy Rate Of Spike Trains Via Lempel-Ziv Complexity, Neural Computation
vol 16 717-736, . 2004
- Bandt C, Pompe B., Permutation entropy: a natural complexity measure
for time series., Phys Rev Lett. 2002 Apr 29;88(17):174102.
- Bhattacharya, J, Complexity analysis of spontaneous EEG, Acta Neurobiol.
Exp. 2000, 60: 495-501
- Burioka, N MD; Germaine Cornélissen, PhD; Franz Halberg, MD; Daniel
T. Kaplan, PhD; Hisashi Suyama, MD; Takanori Sako, MD and Eiji Shimizu, MD,
Approximate
Entropy of Human Respiratory Movement During Eye-Closed Waking and Different
Sleep Stages, Chest. 2003;123:80-86
- Bush SF, Todd Hughes, Ph. D. The Effectiveness of Estimates of Kolmogorov
Complexity to Identify Semantic Types, http://www.atl.external.lmco.com/overview/papers/1172.pdf
2003
- Costa M., Goldberger AL, Peng CK Multiscale entropy analysis of physiologic
time series. Phys Rev Lett 2002; 89:062102
- Costa M, Peng C-K, Goldberger AL, Hausdorff JM. Multiscale entropy analysis
of human gait dynamics. Physica A 2003;330:53-60.
- Costa M, Ary L. Goldberger, and C.-K. Peng, Multiscale entropy analysis
of biological signals. PHYSICAL REVIEW E 71, 021906 s2005d
- Crutchfield JP, D. P. Feldman and C. R. Shalizi. Comment I on ``Simple
Measure for Complexity'' Physical Review E 62(2), 2996-7 (2000).
- Daw, CS, CEA Finney and Tracy ER, A review of symbolic analysis of experimental
data, http://www-chaos.engr.utk.edu/pap/crg-rsi2002.pdf,
2002
- Efstathiou J, S Kariuki, L Huaccho Huatuco, S Sivadasan and A Calinescu,
The relationship between information-theoretic and chaos-theoretic measures
of the complexity of manufacturing systems, http://www.robots.ox.ac.uk/~manufsys/ncmr2001%20janet%20stella.pdf
- Evans S.C., J.E. Hershey and G. Saulnier, Kolmogorov Complexity Estimation
and Analysis, GE Global Research Technical Report, 2002GRC177, October 2002
- Evans, Scott and Bush, Stephen. F. Symbol Compression Ratio for String
Compression and Estimation of Kolmogorov Complexity. Submitted
to 2002 IEEE International Symposium on Information Theory.
- Feldman DP, Jim Crutchfield, A Survey of “Complexity Measures”,
http://www.santafe.edu/~cmg/compmech/tutorials/ComplexityMeasures.pdf
, 1998
- Funes, P. Complexity measures for complex systems and complex objects, http://www.cs.brandeis.edu/~pablo/complex.maker.html
- Fusco G. ; Minelli A., Measuring morphological complexity of segmented
animals: centipedes as model systems; Journal of Evolutionary Biology,
January 2000, vol. 13, no. 1, pp. 38-46(9)
- Gonzalez Andino SL, Grave de Peralta Menendez R, Thut G, Spinelli L, Blanke
O, Michel CM, Seeck M, Landis T., Measuring the complexity of time series:
an application to neurophysiological signals. Hum Brain Mapp. 2000 Sep;11(1):46-57.
- Gu F,, E. Shen, X. Meng, Y. Cao, Z. Cai, Higher Order Complexity Of Time
Series, International Journal of Bifurcation and Chaos V14 #8 pp2979-2990,
Aug. 2004
- Gunther,R; Shapiro,B; Wagner,P; 1994, Complex Systems, complexity measures,
grammars and model inferring, Chaos, Solitons and Fractals, 4, 635-651
- Gusev VD, Nemytikova LA, Chuzhanova NA., On the complexity measures of
genetic sequences, Bioinformatics. 1999 Dec;15(12):994-9.
- Huang L, Fengchi Ju, Enke Zhang, Jingzhi Cheng, Real-time Estimation
of Depth of Anaesthesia Using the Mutual Information of Electroencephalograms,
Proceedings of the 1st International IEEE EMBS Conference on Neural Engineering
Capri Island. Italy March 20-22, 2003
- JänttiV, S. Alahuhta, J. Barnard and J. W. Sleigh, Spectral entropy—what
has it to do with anaesthesia, and the EEG?, British Journal of Anaesthesia,
2004, Vol. 93, No. 1 150-152
- Jones K, Begleiter H, Porjesz B, Wang K, Chorlian D. Complexity measures
of event related potential surface Laplacian data calculated using the wavelet
packet transform.Brain Topogr. 2002 Summer;14(4):333-44.
- Khalatur PG, Novikov VV, Khokhlov AR., Conformation-dependent evolution
of copolymer sequences., Phys Rev E Stat Nonlin Soft Matter Phys. 2003
May;67(5 Pt 1):051901
- Kuusela TA, Tuomas T. Jartti, Kari U. O. Tahvanainen, and Timo J. Kaila,
Nonlinear methods of biosignal analysis in assessing terbutaline-induced
heart rate and blood pressure changes, Am J Physiol Heart Circ Physiol
282: H773-H781, 2002
- Lake DE, Richman JS, Griffin MP, Moorman JR., Sample entropy analysis
of neonatal heart rate variability.Am J Physiol Regul Integr Comp Physiol.
2002 Sep;283(3):R789-97.
- Masum, H; TURING MACHINES AND COMPLEXITY, http://www.carleton.ca/~hmasum/TMandComplexity.html
1995
- Orlov, Y, V.N.Potapov, V.D.Gusev, L.A.Miroshnichenko, Review of the methods
of genetic text complexity analysis, http://wwwmgs.bionet.nsc.ru/mgs/programs/lzcomposer/review.html
- Perakh, M, Defining Complexity, A Commentary to a paper by Charles H.
Bennett, http://www.talkreason.org/articles/complexity.pdf
- Pincus SM, Approximate entropy as a measure of system complexity.Proc
Natl Acad Sci U S A. 1991 March 15; 88(6): 2297–2301.
- Potapov VN, V.D.Gusev, L.A.Miroshnichenko(Nemytikova), Review of the methods
of genetic text complexity analysis, http://wwwmgs2.bionet.nsc.ru:8080/low_complexity/review.jsp
- RADHAKRISHNAN N, JAMES D. WILSON, and PHILIPOS C. LOIZOU, AN ALTERNATE PARTITIONING
TECHNIQUE TO QUANTIFY THE REGULARITY OF COMPLEX TIME SERIES, International
Journal of Bifurcation and Chaos [in Applied Sciences and Engineering], Vol.
10, No. 7 (2000) 1773-1779
- Rapp PE, Cellucci CJ, Korslund KE, Watanabe TA, Jimenez-Montano MA., Effective
normalization of complexity measurements for epoch length and sampling frequency.Phys
Rev E Stat Nonlin Soft Matter Phys. 2001 Jul;64(1 Pt 2):016209
- Rezek I and Roberts SJ,. Stochastic Complexity Measures for Physiological
Signal Analysis. IEEE Transactions on Biomedical Engineering Vol. 44, No 9,
Sept., 1998, pages:1186-1191.
- RICARDO B. R. AZEVEDO, ROLF LOHAUS, VOLKER BRAUN, MARKUS GUMBEL, MURALIKRISHNA
UMAMAHESHWAR, PAUL-MICHAEL AGAPOW, WOUTER HOUTHOOFD, UTE PLATZER, GAËTAN
BORGONIE, HANS-PETER MEINZER and ARMAND M. LEROI, The simplicity of metazoan
cell lineages, Nature 433, 152 - 156 (13 January 2005); doi:10.1038/nature03178
- Richman JS, Moorman JR., Physiological time-series analysis using approximate
entropy and sample entropy. Am J Physiol Heart Circ Physiol. 2000 Jun;278(6):
- Rosso OA, MT Martin, A. Plastino, Brain electrical activity analysis
using wavelet based informational tools, Physica A 313 (2002) 587-609.
- Sasahara, K. and Ikegami, T. (2004) Song Grammars as Complex Sexual Displays.
Ninth International Conference on Artificial Life, September 2004
- Shalizi CR, Causal Architecture, Complexity and Self-Organization in
Time Series and Cellular Automata, Ph.D. thesis, Univ. of Wisconsin, Madison,
Physics Dept., 2001
- Shalizi CR, Kristina Lisa Shalizi, James P. Crutchfield, An Algorithm
for Pattern Discovery in Time Series, http://arxiv.org/abs/cs.LG/0210025
2002
- Shalizi CR, Complexity Measures, http://cscs.umich.edu/~crshalizi/notebooks/complexity-measures.html
2003
- Sleigh JW, E. Olofsen, A. Dahan, J de Goede and A Steyn-Ross. ENTROPIES
OF THE EEG: THE EFFECTS OF GENERAL ANAESTHESIA.
http://phys.waikato.ac.nz/pdfs/cortical/research%20papers/EEG_entropies.pdf
- Szczepanski J, JM Amigo, E Wajnryb and MV Sanchez-Vives, Application
of Lempel–Ziv complexity to the analysis of neural discharges, NETWORK:
COMPUTATION IN NEURAL SYSTEMS, 14 (2003) 335–350
- Torres ME and L. G. Gamero, Relative Complexity Changes in Time Series
using Information Measures, Physica A, Vol. 286, Iss. 3-4, pp.457-473,
Oct. 2000.
- Watanabe TA, Cellucci CJ, Kohegyi E, Bashore TR, Josiassen RC, Greenbaun
NN, Rapp PE. The algorithmic complexity of multichannel EEGs is sensitive
to changes in behavior. Psychophysiology. 2003 Jan;40(1):77-97.
- ZIV J AND ABRAHAM LEMPEL, Compression of Individual Sequences via Variable-Rate
Coding, IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. IT-24, NO. 5, SEPTEMBER
1978
General Sources
Copyright Cornell University, 2005




