A hierarchical graphics modeler using Matlab

Introduction

Designing models of objects is a central part of computer graphics. Quite often it is useful to simulate the physical structure of an obejct to simplifiy design and animation. An example might be an airplane in which the propellers rotate and the whole airplane undergoes rigid body motion as it takes off. It would be annoying to have to separately remember to move every part of the airplane, even though the airplane might be made up of dozens of geometric objects. More information can be found by searching the keywords: computer graphics hierarchical modeling. A few references are given at the end. The following paragraphs describe a system to produce simple models of objects then combine and animate them. The models are produced by two methods:

Programming model for Surfaces

The method used here is to package each geometric primitive (e.g. sphere) as a Matlab 'struct'. Geometric primitives are then grouped in a 'cell array'. The cell array is ultimately passed to the renderpatch function for conversion to a shaded polygon image or the renderwire function for conversion to a wireframe image.

Each geometric primitive struct may have several data fields. Each struct must have a faces field and a vertices field in order to be rendered. The vertices field of N vertices must be an Nx3 array. The faces field of M faces must be an Mxf array, where f would be 3 for a triangle list and 4 for a rectangle list. For example a struct called cube could be defined as: 

cube.vertices=[ 0 0 0; 1 0 0; 1 1 0; 0 1 0; ...
                0 0 1; 1 0 1; 1 1 1; 0 1 1;]; 


cube.faces=[ 1 2 6 5; 2 3 7 6; 3 4 8 7; ...
             4 1 5 8; 1 2 3 4; 5 6 7 8; ] ;

Of course, it would be tedious to have to figure out the faces for spheres and other objects, so a set of prototype objects is included below.

There are several optional fields which can be defined. The field names are case-sensitive and must be all lower-case. If you do not specify a field value, its default value is used. All fields can be used with the renderpatch function. Only facecolor, edgecolor and visible may be used with renderwire. In addition, renderwire maps the facecolor to the edgecolor.

For instance for the cube struct you might want to specify

cube.facelighting='flat';   %flat shading with no edge interp 
cube.facecolor=[.9,.2,.2];  %a red color

The renderers, renderpatch and renderwire expect a cell array as a parameter. The cell array should contain all objects to be rendered. The combine function described below concatenates objects in the correct format for the renderers. See the example code below for specific use.

The Matlab Code for Surfaces

The code is packaged as several Matlab functions so that is can be used in a natural fashion. The Matlab 'help' function will return information on each function.

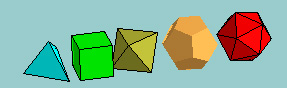
Examples using Surfaces

  1. This short example draws a three segment arm-like device and rotates each segment. 
    cyl = UnitCylinder(2);
 
L1 = 3;
L2 = 2;
L3 = 1;
radius = .3;
 
w1 = 5;
w2 = 10;
w3 = 30;
 
arm1 = translate(scale(cyl,radius,radius,L1/2),0,0,L1/2);
arm1.facecolor = 'blue';
arm2 = translate(scale(cyl,radius,radius,L2/2),0,0,L2/2);
arm2.facecolor = 'green';
arm3 = translate(scale(cyl,radius,radius,L3/2),0,0,L3/2);
arm3.facecolor = 'red';
 
angle1 = 0 ; angle2 = 0 ; angle3 = 0;
 
for i = 1:36
    
    distal = combine(translate(rotateY(arm3,angle3),0,0,L2),arm2);
    distal = rotateY(distal, angle2);
    
    arm = combine(translate(distal,0,0,L1), arm1);
    arm = rotateY(arm, angle1);
    
    cla
    renderpatch(arm);
    camlight
    box on
    view(30,30)
    drawnow
    set(gca,'xlim',[-5 5],'ylim',[-5 5],'zlim',[-5 5])
    
    
    angle1 = angle1 + w1 ;
    angle2 = angle2 + w2 ;
    angle3 = angle3 + w3 ;
end

  2. This program builds a water molecule, duplicates it, then flys the camera around the scene and makes a movie of the flight. 
    clear all
 
% Hydrogen 
H = UnitSphere(2);
H.facecolor = 'blue';

%Oxygen 
Rox = 1.4;
Ox = scale(UnitSphere(2),Rox,Rox,Rox);
Ox.facecolor = 'red';
 
d = 1.4;   %approx O-H distance
H1 = translate(H,d,0,0);
ang = 107; %bond angle
H2 = rotateY(H1,ang);
 
water = combine(Ox,H1,H2);
 
%approx Hydrogen bond distance
water2 = combine(water,translate(rotateX(water,-45),1,2,3));
 
%init 40 frames of a movie
mov = moviein(40);
framecount = 1;
figure(1); clf;
%draw the water and move the camera and make a movie
for i=0:.1:1.57
    renderpatch(water2);
    camlight
    set(gca,'cameraposition',[20*cos(i),20*sin(i),0])
    set(gca,'cameratarget',[1,1,1])
    set(gca,'cameraupvector',[0 0 1])
    set(gca,'cameraviewangle',30)
    set(gca,'xlim',[-5 5],'ylim',[-5 5],'zlim',[-5 5])
    box on
    xlabel('x')
    ylabel('y')
    zlabel('z')
    mov(framecount) = getframe(gcf);
    framecount = framecount + 1;
end
 
figure(2); clf;
axis off
movie(mov,-5,15);

  3. The following code renders the image at the top of the page. 
    clear all;
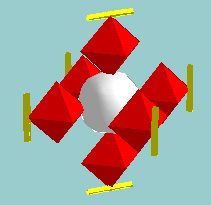
clf;

sphere1=UnitSphere(2);
sphere1.facecolor='white';

cyl1=UnitCylinder(1);
cyl1=translate(scale(cyl1,.1,.1,.75),2.8,0,0);
cyl1.facelighting='flat';
cyl1.facecolor='yellow';

octa1=UnitSphere(1);
octa1.facecolor='red';
octa1.facelighting='flat';
octa1.specularstrength=.7;
octa1=translate(octa1,1.8,0,0);

%Animate
for time=0:.1:4
   
   level2=combine(...
      rotateX(octa1,time*90), ...
      rotateX(cyl1, time*(-180)) );
   
   level1=combine(...
      level2, ...
      rotateY(level2,90), ...
      rotateY(level2,-90), ...
      rotateY(level2,180), ...
      rotateZ(level2,90), ...
      rotateZ(level2,-90)...
      );
   
   base=rotateZ(combine(sphere1,level1),time*45);
   
   clf
   count=renderpatch(base);
   axis off;
   grid on
   daspect([1 1 1])
   
   light('position',[10,-10,10])
      
   %Do a persptective transform
   set(gca,'projection','perspective')
   set(gca,'CameraViewAngle',6)
   
   %The frame background color
   set(gcf,'color', [.6,.8,.8])
   xlabel('x');ylabel('y');zlabel('z'); 
   view(-28,20)
   drawnow;
   
end %for  

rotate3d on

  4. This example constructs a simple airplane and rotates the props. Setting cockpit.facealpha=0.6 results in a transparent cockpit canopy.

  5. The UnitSphere, UnitTorus, and UnitCylinder shapes can be parametrically modified using a 'superquadric' formulation which results in 'squared off' shapes. Example images show the effect applied to a sphere and a torus.

  6. A student and I used this modeling system to build a simple maze. The maze was presented as both an overhead and in-the-maze view. We made a simple GUI to navigate the maze. There are two files necessary to run this example; maze6.m and maze6key.m. The first program defines the maze and a bunch of UIcontrols (see GUI design). The second program is a function which is called to implement camera movement through the maze. An example of the two views is shown below. The maze consists of a collection of scaled UnitCubes which are translated to various positions.

Constructive Solid Geometry (CSG)

The CSG description used here is very simple and limited to fairly coarse volume representations of solids. The scheme is to represent each elementary solid, e.g. cube, as a 3D field of values, negative on the inside and positive outside. The CSG operations of union, intersection, and subtraction then become simple min/max operations on the 3D fields. After all CSG operations are complete, the volume representation is converted to surfaces.

Programming model for CSG

All volume-shapes are generated as 3D scalar fields. These fields may be subjected to the usual CSG operations mentioned above. Since fields are really arrays, all fields which are to be combined must have the same number of elements. The 'resolution' parameter associated with construction of CSG objects sets the number of elements and thus must be the same for all CSG objects which will be combined using CSG operations. After all CSG operations are performed, the volume-object is converted to surfaces for rendering. The volume which is modeled by the CSG operations is hardcoded to -1 to +1 on each axis. Objects may be scaled after they are converted to surfaces. Objects may also have other parameters, such as facecolor, set after they are converted to surfaces. All objects are rendered using the routines described above.

You may use several distinct CSG objects in a scene. Each different object can have its own resolution.

Matlab code for CSG

As with surfaces, there are routines to build and modify CSG objects.

Examples Using CSG objects

The following code produces a cup sitting on a simple table as shown below.

%build a cup sitting on a table


clear all
clf


res=15 ;

%build the cup body
%by making a closed-end cylinder
cyl1=CSGcylinder(0,0,0,.45,'z',res);
cube1=CSGcube(0,0,-.5,.5,res);
body=CSGintersection(cyl1,cube1);
%then subtracting another, smaller cylinder
cyl2=CSGcylinder(0,0,0,.35,'z',res);
cube2=CSGcube(0,0,-.4,.4,res);
hole=CSGintersection(cyl2,cube2);
body=CSGsubtract(body,hole);


%make the handle
s1=CSGsphere(.6,0,-.4,.3,res);
cyl3=CSGcylinder(.6,0,-.4,.15,'y',res);
handle=CSGsubtract(s1,cyl3);


%join handle and body to make the cup
cup=CSGunion(body,handle);
cupSurface=CSGtoSurface(cup,res);
cupSurface.facecolor='yellow';


%now make a place to set the cup
table=UnitCube;
table.facecolor=[1,.6,.6];
table.facelighting='flat';
table.edgecolor='red';
table=scale(table,1,1,.2);
table=translate(table,0,0,-1.2);

scene=combine(cupSurface, table);

count=renderpatch(scene)

   axis off;
   grid on
   daspect([1 1 1])
   
   light('position',[10,0,10])
   %light('position',[10, 10, 10])
   
   %Do a persptective transform
   set(gca,'projection','perspective')
   set(gca,'CameraViewAngle',8)
   
   %The frame background color
   set(gcf,'color', [.6,.8,.8])
   xlabel('x');ylabel('y');zlabel('z'); 
   view(7,20)
   drawnow  

rotate3d on

3D camera model

I started writing low level graphics code in Matlab a few years ago with the idea of using it in an introductory graphics course. The GUI and an associated function convert a 3D face list and vertex list into a 2D image. Put the GUI and associated funciton in the same folder and run the GUI.

 

References

Computer Graphics: Principles and Practice in C, James D Foley

Computer Graphics, Fall 2000 Thomas Funkhouser Department of Computer Science Princeton University