Background
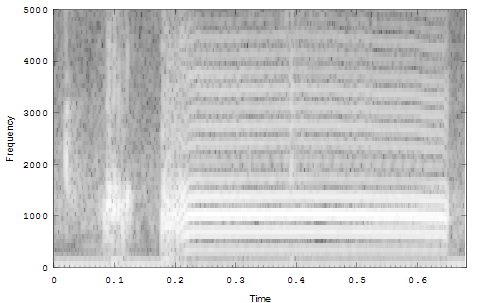
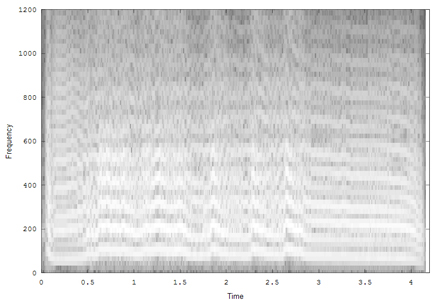
The sound spectrogram is a mainstay of sound analysis. A plot of intensity at each frequency and time yields information about the spectral content of nonstationary signals. There is an inherent tradoff between frequency resolution and time resolution. The power spectrum of a short-term FFT (STFT) over T seconds cannot resolve events happening faster than T, nor can it resolve frequency differences smaller than 1/T. A loon call (from Charlie Walcott) at two difference lengths is an example. The calls were sampled at 22050 samples/second and spectrogram formed using STFT length of 256 and 1024. Frequency features are better resolved in the longer transform and time features better resolved in the shorter. It would be nice to have the best of both worlds. It is possible to get better resolution, within limits, by using more information than just the power spectrum.
A technique for sharpening the
spectrogram uses information from the phase spectrum to sharpen the amplitude spectrum.
The scheme locates simple sinusoids, linear chirps, and impulses at the correct frequency or
time with a higher resolution than the inherent FFT resolution tradeoffs. The basis of the calculation is that the
instantaneous frequency (IF) in each FFT frequency band is equal to the first time derivitive
of the short-term FFT (STFT) phase at frequency ω and time T:
IF = ∂/∂t(arg(STFT(ω,T)))
and the local group delay (GD) at frequency ω and time T is approximately
GD = ∂/∂ω(arg(STFT(ω,T)))
where the function arg returns the phase angle of the transform (see Fulop).

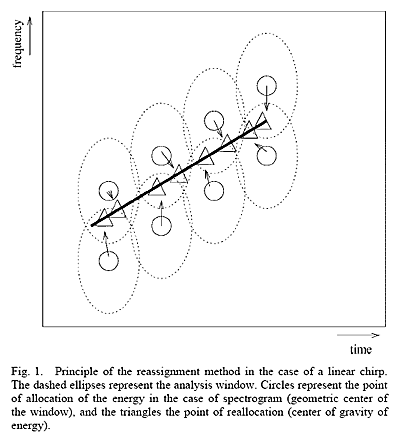
Chassande-Mottin, et.al. show that reassignment is equivalent to moving energy up the local gradient of intensity of the spectrogram (for Gaussian windows). This higher precision does not violate basic time/frequency uncertainty (see Gardner and Magnasco). There is still mixing between reassigned frequencies or impulses which are close together. Plante, et.al. illustrate this with a nice figure shown to the left. Each elipse represents one frequency-time cell of the STFTs which make up a spectrogram. The energy in the cell is is placed at a location determined by the IF and GD.
An online matlab reassignmentt code (Fitz, 2008) was modified for faster rendering and more straightforward selection of minimum plotting amplitude and rendering method. The modified raspecgram and ratoplot (called by raspecgram) produce a reassigned spectrogram, but require a few other routines from the Fitz site. The code runs in Gnu Octave as well as matlab. There is also reassignment code at mathworks.
Examples show the effect of the reassignment.
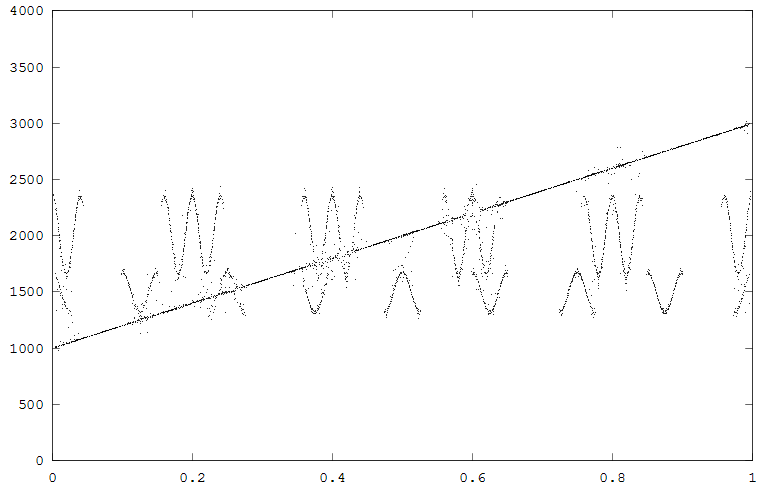
The first example generates two FM signals, with a superimposed linear chirp. The waveform and spectrogram are shown the the first figure, the reassigned spectrum in the second figure. Note that in much of the reassigned plot the FM signals and chirp are well localized, but when they approach each other some scattering occurs. Scattering can be optimized (as usual in a spectrogram) by changing the size and overlap of the FFTs used to produce the results. The reassigned spectrogram was rendered using one color for all points above an energy amplitude cutoff. The rendering mode is refered to in the code as fast. The rendering mode format is method_size_marker. For instance fast_1_dot, color_3_circle, color_1_circle are all valid. Valid methods are fast/color. Valid markers are dot/circle.
Waveform and spectrogram of the test signal.

Reassigned spectrrogram of the test signal.
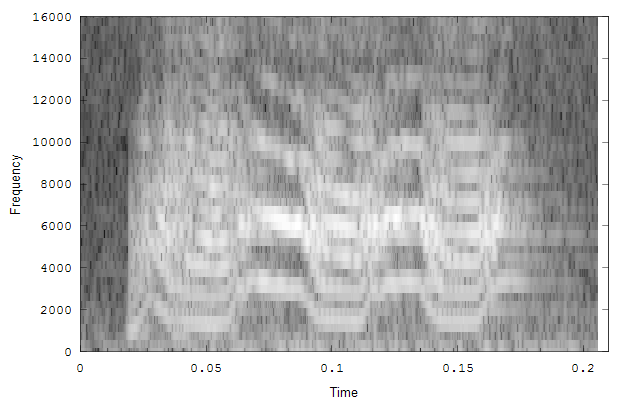
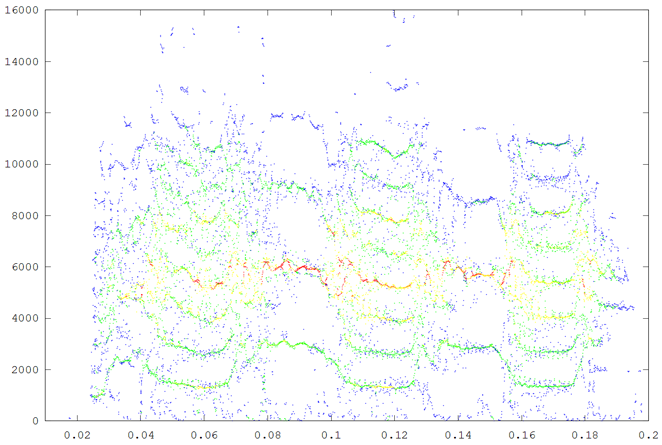
The second example is a nestling green-rumped parrotlet (Forpus passerinus) begging call (thanks to Karl Berg) with a complex multiharmonic, FM structure. The spectrogram of a short segment is shown in the first figure, the reassigned spectrum of one vocal burst in the second figure and another in the third figure. The reassigned spectrogram shows a lot of detailed FM which is hard to discriminate in the original spectrogram. There is enough similarity between the two vocal bursts (and enough coherent structure in each image) to suggest that much of the fine detail revealed is real. The reassigned spectrogram was rendered using four colors for points in four log(energy) bins above an energy amplitude cutoff. Red is highest energy, then yellow, green and blue. The rendering mode is refered to in the code as color_1_dot.
Spectrogram of a short segment of the parrot song.
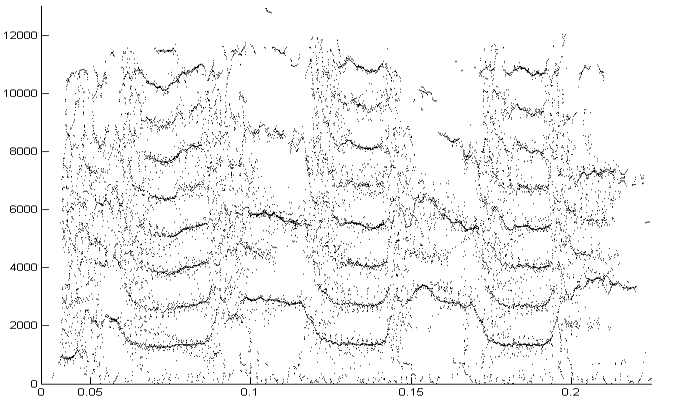
Reassigned spectrogram of the above segment
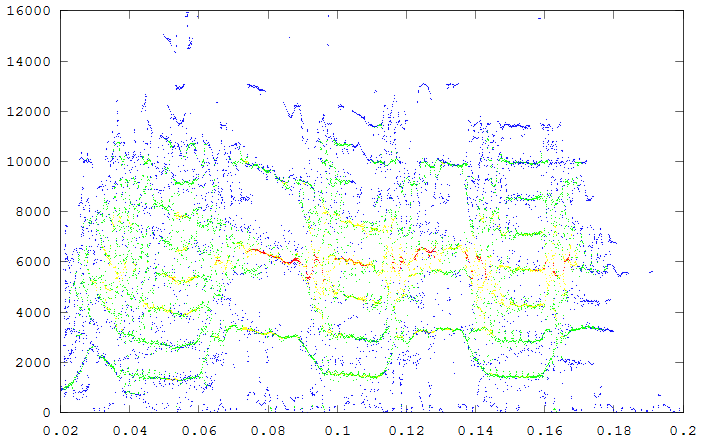
A second segment of the same song to show repeatbility. (click to enlarge)
The third example is a boat-whistle call of the gulf toadfish (Opsanus beta) (Thanks to Luke Remage-Healey and Aaron Rice). The sound is a short noise burst followed after a pause by steady, harmonic-rich hoot. The image pair shows a short segment analysed with a 512 point STFT and 90% overlap of STFTs. The standard spectrogram is to the left and reassigned spectrogram to the right (click to enlarge).

The fourth example is Midshipman growl. The three images (all clickable for more resolution) show the spectrogram (2048 point FFT, overlap of 0.9), reassigned spectrogram, color coded by intensity, and an overlay of all the reassigned points superimposed on the spectrogram.
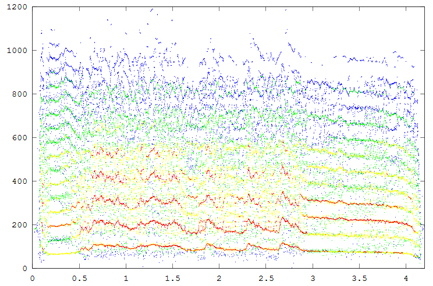
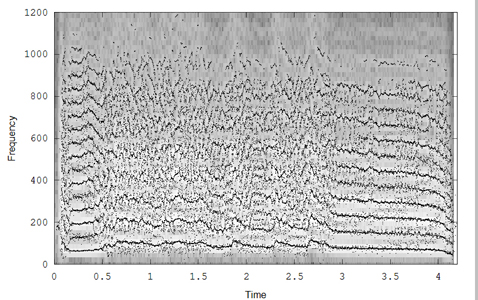
A further modification of the reassignment code, raspecgram, modifies the way data is returned to make it easier to interface further analysis. A first attempt at producing error bands for the reassigned energy does the following:
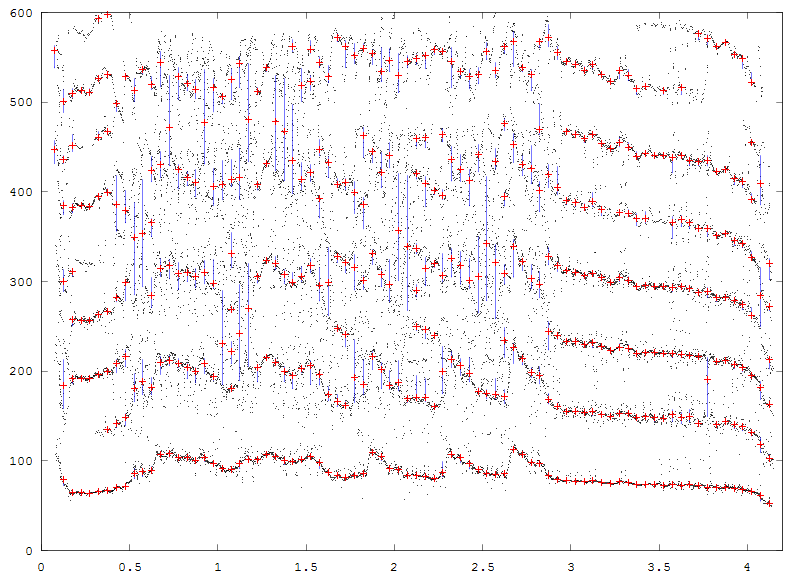
The output of an example program is shown below. The medians are red crosses, the quartile ranges plotted as blue lines. The time bin is 0.05 seconds, the gap detected is 0.5*(FFT freq bin) and the minimum number in a group is 15. The signal is the same as the previous example.
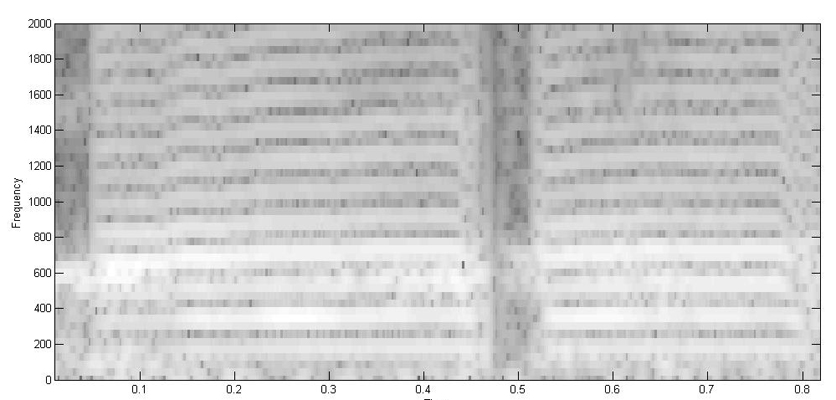
A fifth example is from an electric fish.
Waveform:

Spectrogram:

Reassigned:

Another example is from a toadfish agonistic call. The fish has two different size swimbladders. (Rice and Bass 2009)
Spectrogram:
Reassignment 1024 FFT
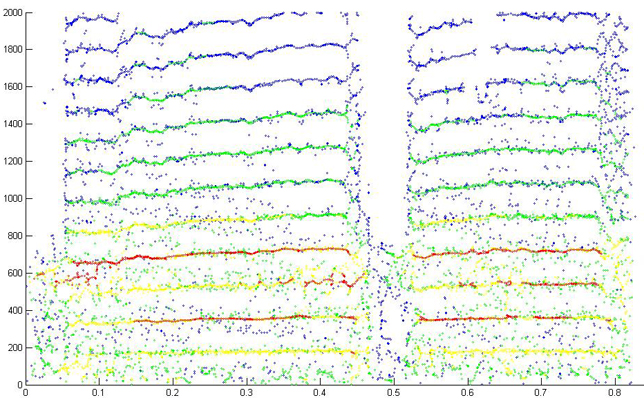
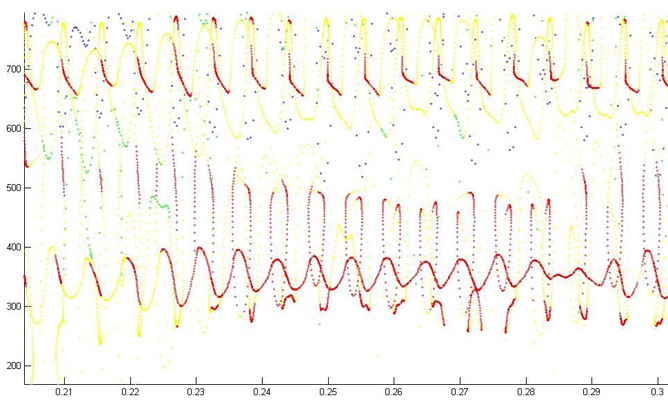
Reassignment detail with more overlap 256 FFT
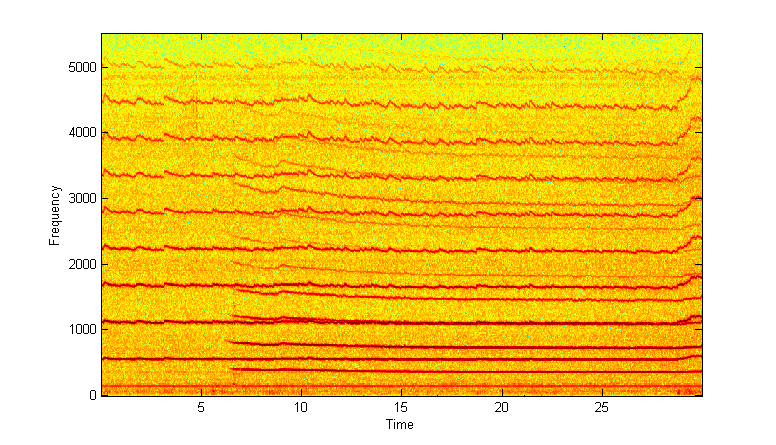
Mosquito harmonic convergence (Lauren J. Cator, et.al.) data frm BJA. Male and female match the male's second harmonic to the female's third harmonic. Details of frequency tracking may be better seen using RA techniques.
Spectrogram
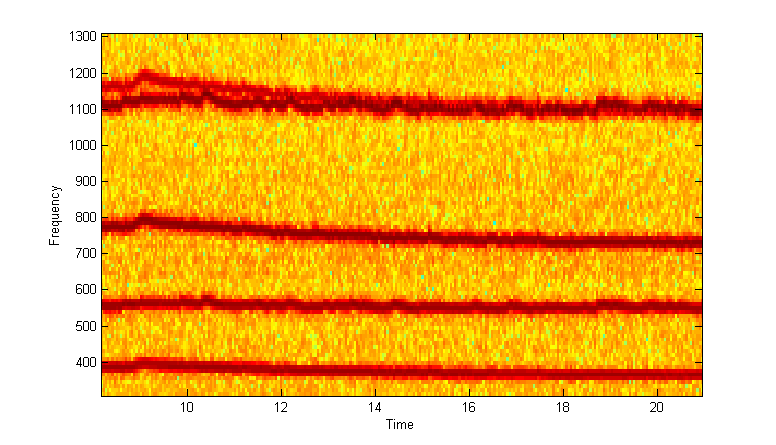
RA set at 1024 sample FFT and 90% overlap

Zoomed versions to show overlapped harmonics and fundamentals.
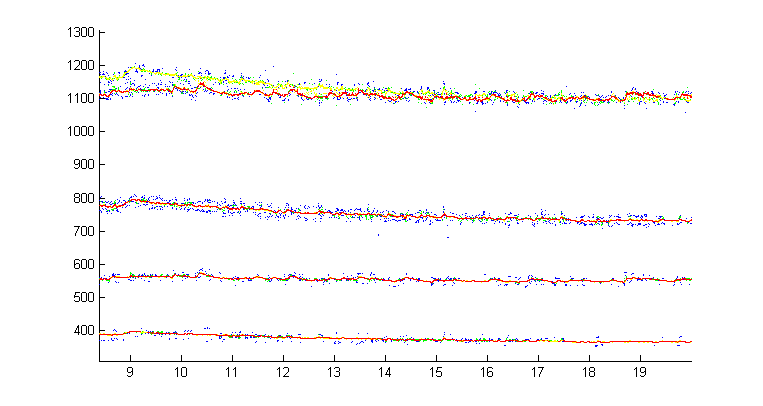
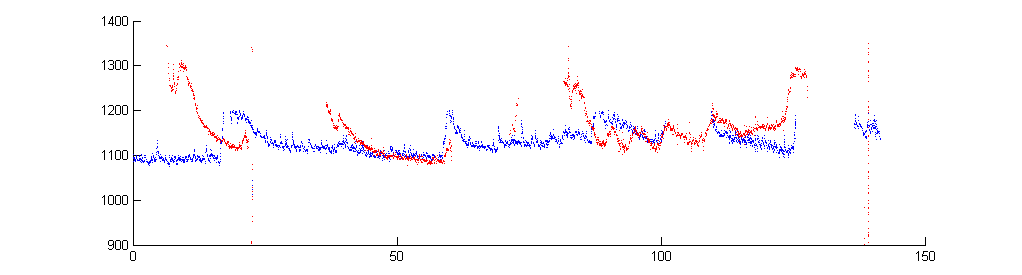
In the next image, the male and female fundamentals were isolated based on frequency for the whole song, then the male fundamental was multiplied by 2 and colored blue, while the female fundamental was multiplied by 3 and colored red. It is much easier to see the overlaps and trajectories of the two sounds (including the best tracking in this sample around 50 seconds). Code is here.
References:
Kelly Fitz, Time-Frequency Analysis, 2008. Site includes code distributed under GNU public license.
Stephen Hainsworth, Malcolm Macleod, Stephen W. Hainsworth, Malcolm D. , Time Frequency Reassignment: A Review and Analysis, Macleodhttp://www-sigproc.eng.cam.ac.uk/~swh21/tfrrep.pdf ---or--- S.W. Hainsworth and M.D. Macleod, Time-frequency reassignment: a review and analysis, Tech. Rep. CUED/FINFENG/TR.459, Cambridge University Engineering Department, 2003.
E. Chassande-Mottin, I. Daubechies, F. Auger and P. Flandrin, Differential Reassignment, IEEE SIGNAL PROCESSING LETTERS, VOL. 4, NO. 10, OCTOBER 1997
Fulop, Sean A., Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications, The Journal of the Acoustical Society of America, vol. 119, issue 1, p. 360
F Plante, G Meyer, WA Ainsworth, Improvement of speech spectrogram accuracy by the method of reassignment, Speech and Audio Processing, IEEE Transactions on, Vol. 6, No. 3. (1998), pp. 282-287.
Timothy J. Gardner and Marcelo O. Magnasco, Sparse time-frequency representations, PNAS, vol 103 #16, pp 6094-6099, www.pnas.org/cgi/doi/10.1073/pnas.0601707103
Lauren J. Cator, Ben J. Arthur, Laura C. Harrington, Ronald R. Hoy, Harmonic Convergence in the Love Songs of the Dengue Vector Mosquito, Science DOI: 10.1126/science.1166541
Rice, A. N., and A. H. Bass. 2009. Novel vocal repertoire and paired swimbladders of the three-spined toadfish, Batrachomoeus trispinosus: insights into the diversity of the Batrachoididae. Journal of Experimental Biology 212:1377-1391.
Copyright Cornell University, 2008