Spike Train Analysis of Fictive Vocalization and Auditory Efferents.

Matt Weeg, Bruce Land, Andy Bass

Introduction

We wanted to investigate the relationship between action potentials occuring in the motor nerve controlling vocal production in the plainfin midshipman and action potentials occuring in the auditory nerve. The relationship could have implecations for gain control of the ear during vocalization.

The process

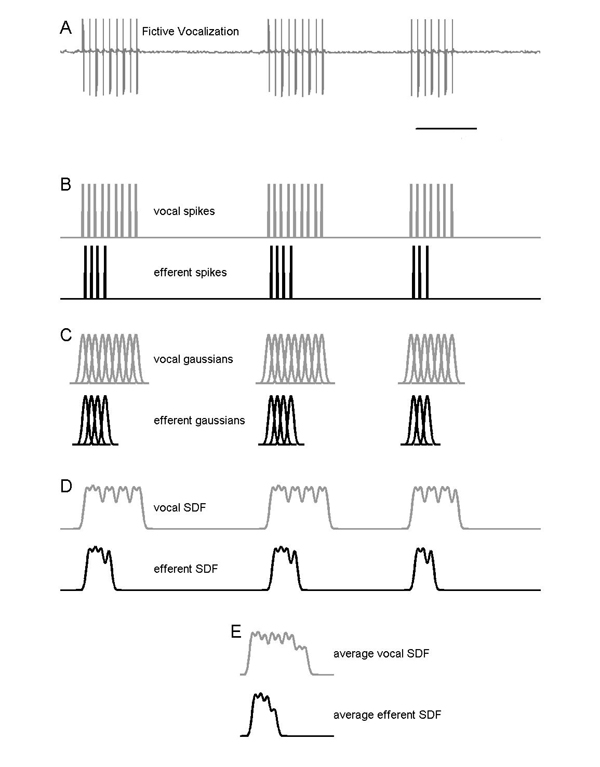
When vocally active sites within the midbrain were stumulated with glutamate, motor neurons produced a series of fictive grunts. Simultaneous recording from the auditory nerve often showed correlated efferent activity. Recordings could include as many as 70 fictive grunts from each motor neuron, and associated auditory nerve efferent activity. To ensure unbiased interpretation and to automate data analysis, we designed a procedure to produce an average vocalization spike activity and a synchronized average efferent activity. To do this we needed to align the start (or end) of each vocalization. Then we averaged spikes across all the aligned vocalizations. the begining (or end) time of the vocalization was used as a reference to align the efferent activity for each fictive grunt.

We tried several schemes to accomplish the alignment. First we tried using the first spike in a fictive vocalization as a trigger for a 'post trigger histogram'. this did not produce satisfactory results be cause the narrow bin width necessary to resolve the temporal structure caused excessave aliasing (due to bin edge effects). We settled on a spike density function (SDF) scheme because we could control the degree of smoothing and because the Gaussian we used as the SDF kernel is very good at reducing aliasing. The following figure shows the process we used. The data shown in the figure is typical of data we recorded, but is synthesized calibration data.

The steps in the process:

  1. Recording of action potentials from the vocal motor nerve.
  2. The upper panel is a spike train isolated by thresholding from A.The lower panel are hypothetical efferent spikes, which are shifted copies of the vocal spikes meant to approximate the phase-locking we saw in the real data.
  3. In order to average together spike occurances in several grunts each spike was replaced by a gaussian for summing. The width of the Gaussian was chosen to minimize the ripple on the SDF.
  4. The summed Gaussians form the SDFs.
  5. The average SDF is calculated by aligning the vocal and efferent SDFs (in this case three vocalizations) based on the start time of the vocal SDF. Alignment was determined by locating the 50% point on the rising phase of each vocal SDF and shifting all of the vocal and efferent SDFs accordingly.

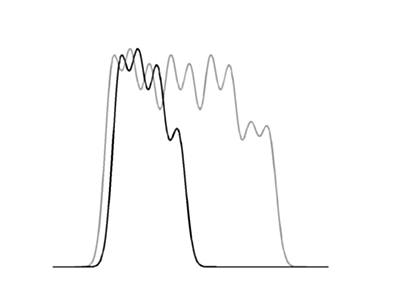
Expanding the time scale of E above and overlaping the traces, you can see below that the time of average occurance of efferent spikes are shifted in time relative to the vocal spikes. In this example, the efferent spikes were just shifted copies of the vocal spikes and were all shifted the same amount in order to check the averaging algorithm. The shift was equal to 1/2 of the first vocal ISI. The real efferent data shows a more interesting pattern of phase-locking.

The programs

All programming was done in Matlab 6.5 from the Mathworks. The program does the following operations:

  1. Read all the data from one neuron. The data was in a text format consisting of header infromation and lists of spike arrival times for each of several time sequences. Some time sequences had no spikes.
  2. Plot the raw spike times for visual cross check
  3. Make the SDFs using a fairly wide kernel (5 mSec) and find the starting times of the fictive grunts. Staring times were defined as the point where the SDF crossed 50% of the peak SDF in the specific time sequence. The kernel was computed using the following code for a Gaussian with unit area. The Gaussian was arbitraily truncated to zero after +/-3 standard deviations. Spike trains were rasterized at a resolution of 1 mSec for convolution with Gaussians. 
    vocwidth = 5;
voctk = -3*vocwidth:3*vocwidth ;
vockernel = exp(-(voctk/vocwidth).^2/2)/(vocwidth*sqrt(2*pi));
  4. Remake the SDFs using a narrow kernel for good time resolution (2 mSec), use the start times from 3, and average the SDFs.
  5. In all cases, width of the kernel used to calculate the SDF was the same for the vocal and efferent spike trains.
  6. Plot the average SDFs.

Reference:

Weeg MS, Land BR, Bass AH (2005) Vocal Pathways Modulate Efferent Neurons to the Inner Ear and Lateral Line, Journal of Neuroscience, June 22, 2005, 25(25):5967–5974 (pdf)

Copyright Cornell University, 2004