ECE 476 Spring 2008 Final Project: Battle Tank - A 3d Atmega32 Based Video Game
Matthew Ito (mmi4), Jsoon Kim (jk459)
Introduction
Our project is a wireframe 3D video game based on the classic Atari arcade game, Battlezone (Copyright Atari Corp, 1980).
For those that have never heard of the game, Battlezone is a game in which the player maneuvers a tank through a flat environment, shooting and destroying enemy tanks while taking advantage of obstacles. Objects on the screen are rendered in wireframe 3D. The original game runs on a 1MHz, 8-bit Motorola 6502 MCU, and we figured we would be able to run a similar game on the 16MHz 8-bit Atmel ATMega32 MCU that we have been using all semester. Unfortunately, we did not take into account the corresponding hardware which literally drew the vectors onto the screen (controlled an electron gun and generated the image based upon vector commands input to specialized hardware), as well as the SRAM constraints and processing constraints which would pop up repeatedly. Thus, although our project does implement a basic 3d vector engine on the ATMega32, our project is much scaled back from our initial vision.

Figure 1: Screenshot from original Battlezone.
CAUTION: Although we have worked to minimize video flicker, patterns of flicker may still result at certain points. Those who are photosensitive should exercise caution when attempting to operate our project. Also, eyestrain may result from continuous play, please take time to rest with every interval of play.
High Level Design
The primary inspiration for our project stems from the classic 1980's arcade game, Battlezone. As the hardware it was implemented on seemed basic, we thought that we could pull off something similar with the ATMEGA32 MCU. As mentioned above, significant changes had to be made as we realized the scope of the initial project.
The game runs on a simple wireframe 3D engine that we wrote. The following is a discussion of the basics of 3D rendering in relation to our engine.
Projecting the Game Objects onto the Screen:
In our implementation, game objects are represented by arrays of vertices (points) and edges forming polygons shaped as tanks, terrain obstacles, bullets, etc. This was our initial implementation - the final project differs from this, as mentioned later. The objects exist in 3D space, and are projected onto the television screen, a 128 by 100 2D space (in the actual implementation, we use only a fraction of this space to speed up processing and thus reduce screen artifacts).
The camera is fixed at the point (0,0,0), and points in the -z direction (we ended up pointing the camera in the +z direction in the actual implementation, the following figures were drawn prior to the change and thus point in the –z direction). The distance between the virtual camera and the screen is d. The width of the screen is 128 and the height of the screen is 100. Since the width of the screen is fixed, the viewing angle, shown as 2θ, is adjusted by adjusting d. The following figure illustrates the projection of a simple edge whose points have coordinates at (x1,y1,z1) and (x2,y2,z1), where z1 is negative and greater than the distance between the screen and the camera.
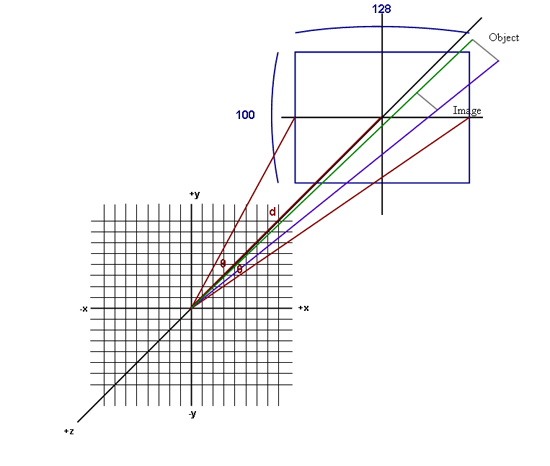
Figure 2: The blue rectangle represents the screen. The red lines are drawn between the camera at the origin and the screen. The object and its projection onto the screen are drawn in gray. A green line and a purple line each connect one of the two points of the object to the camera at the origin, illustrating how the projection onto the screen is obtained.
To project the object onto the screen, the vertices (x1,y1,z1) and (x2,y2,z1) are taken and converted to the points (x1',y1') and (x2',y2'). The formula for this tranform is simple - the x and the y components are scaled based upon their "distance" to the virtual camera, and a screen scaling terms which changes how much of the screen is viewed by the "camera":
x' = (x*d)/(z-zofCamera)
where x is the previous x coordinate, d is the aforementioned scaling factor, z is the object's distance from the camera, and zofCamera is the camera's location along the Z axis.
As zofCamera in this case is equal to zero, the formula collapses to:
x' = (x*d)/(z).
The formula can be just as easily applied by substituting the Y term in for X, after which our x and y points are transformed into a basic camera perspective mapping. A line is then rendered between points (x1',y1') and (x2',y2') to complete the projection. The line draw algorithm we used is the same one utilized by Bruce Land's code, which used a general Bresenham algorithm in order to determine the correct points to draw for a line. A short explanation of the basic algorithm follows.
Basic Bresenham algorithm: Start at a fixed x, and fixed y, and a fixed x,y endpoint. Calculate the dy/dx, and use it to calculate an error term. Increment the error term by dy/dx, increment the x row by 1, draw pixels in the correct direction, incrementing y, until the error between the calculated y term and the actual y term is zero, increment the error term by dy/dx, increment the x term by 1, and continue the algorithm until the given endpoint is reached, and a roughly optimal rasterized line will be drawn along a specified 2-space line.
The following figure provides an illustration of the aforementioned projection algorithm. The calculation of the x coordinate of the upper left vertex of the edge projected onto the screen. First, the horizontal and vertical green lines anchor the point and its projection onto x and y coordinate axes (drawn in black) at appropriate distances z. The intersection of the green line drawn between the point and the camera with the plane of the screen is the point we are trying to calculate.
A simple method to do so is to project the vertex onto the x axis, obtaining the point (x1,0,z1). Then, we draw a line from that projected point to the camera. The x value of the intersection of the line drawn from (x1,0,z1) to the camera with the screen plane will have the same x coordinate as the intersection of the line drawn between the original point (x1,y1,z1) and the camera with the screen plane, as can be seen from the figure below. We can draw two similar triangles (which are drawn in red) to calculate the x coordinate of the projection onto the screen.
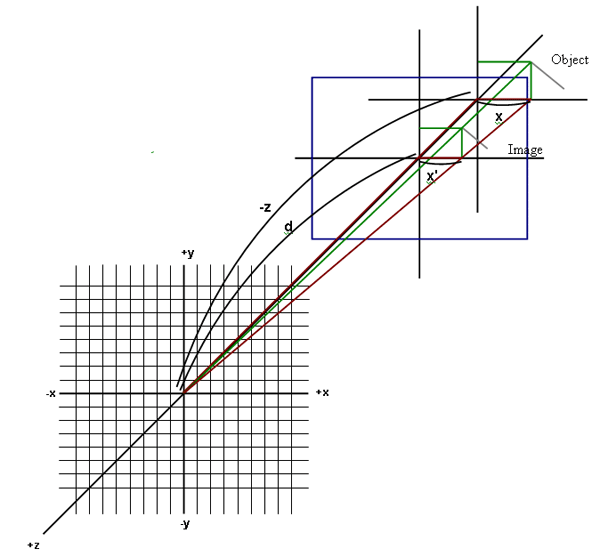
Figure 3: An illustration of a projected line.
Thus, an object with n vertices requires 2n multiplications and 2n divisions to obtain the vertices of the projected image, from which each corresponding edge must be rendered. The multiplications can be substituted with much faster shift operations if d is set to a power of 2. We attempted to implement this optimization in our code, in order to speed processing. Also, note that this method works for edges whose vertices have different z coordinates (the projected line will be skewed appropriately) and for objects with a z distance between the camera and the screen (the projected line will appear stretched on the screen). Finally, in the example above, we fixed the camera at the origin, but the exact same method can be used to find projections for cameras located elsewhere on the z axis.
Using Matrix Transforms:
The figure below illustrates a bird's eye view of the game field at one point in time. The green square represents the player tank, the magenta tanks represent the enemy tanks (the tanks ended up not being completely implemented in the final project, so substitute "target" for tank), the green circle represents a player projectile, and the magenta circle represents an enemy projectile. The red and blue lines represent the player's angle of view and the screen. The blue line is 128 units long in the x direction, and on it, an object with width n units will appear as n pixels wide.
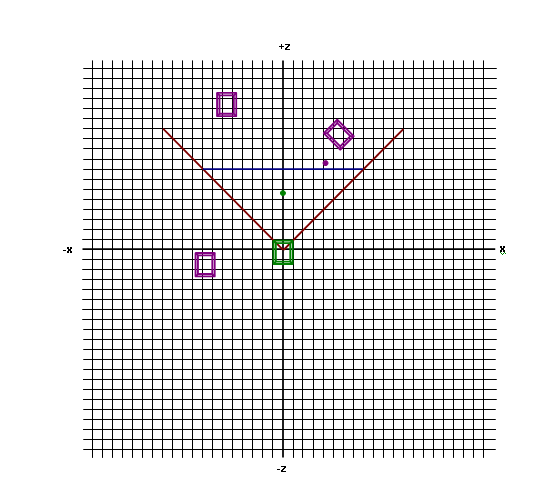
Figure 4: Example of a player tank, as well as the view space.
The camera, and hence the player's "tank", is fixed at the origin to prevent any unnecessarily complicated calculations, and hence, player inputs will move every other object in the game instead of moving the player tank. A forward move will translate all objects downwards (from the bird’s eye perspective), towards the -z direction. A backward move will likewise translate all objects toward the +z direction. This can all be performed by matrix multiplication. An example follows:
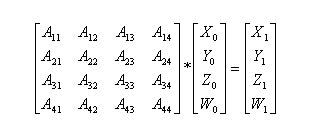
Figure 5: An example of a matrix multiplication in 4x4.
Where A is the transform matrix, x,y and z are cartesian coordinates, and w is a homogeneity term which allows for arbitrary non-linear transforms (in this case, since we translate our vertex by constant terms, we simplify by assuming that W is always equal to 1). By substituting entries into the various A entries, we can perform any sort of transform we wish on the X,Y, and Z terms. The translation of coordinates (x,y,z) by rotation around the X-Z plane is performed by the following matrix equation:
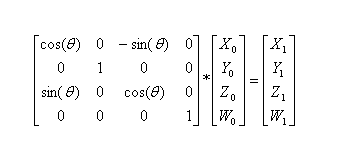
Figure 6: An example of a rotation matrix.
Thus, 16 multiplications (significant cycles) and 12 additions (negligible in terms of performance impact) are required to transform one vertex. However, observing the above two equations, we see that some multiplications and additions are not required for our purposes. Since the y coordinate remains constant for all of our objects (no objects in our game move up or down), the entire series of multiplications to obtain the y coordinate after the transform is unnecessary, and we can simply have y be constant throughout the transform. This reduces the number of multiplications by 4. Similarly, the homogeneous W (the 4th term) is always 1, so we can get rid of those multiplications as well, reducing the number of multiplications by 4. Note that W is required for translating coordinates (see the first matrix equation above), so we just can’t get rid of the coordinate itself and reduce everything to a 3x3 by 3x1 matrix multiplication. Finally, when we calculate the x coordinate after the transform, we have one multiplication involving the “fourth coordinate,” and the same when we calculate the z coordinate after the transform. Since multiplication of any number by 1 equals the number, we can get rid of those two multiplications as well. We are left with only 6 multiplications per vertex transform. The additional W term in the matrix also allows us the freedom to combine a translation with a rotation without a necessary multiplication of the two matricies, as the W term will always be 1, so we can simply place the translation into the rotation matrix and the vertex will exhibit the correct translation behavior.
Additional Comments:
With regards to the line drawing algorithm, we also utilized a basic clipping algorithm. The first part of the clipping algorithm ensures that Z>abs(X), for any verticies called. This ensures that the line lies within the forward view of the window, approximately 90 degrees wide. The second is to ensure that post-perspective transform, that we do not render any lines outside of the screen. We check each endpoint to see if the endpoint lies within the projection onto the screen, and if they lie outside, we do not render them. If any lines are written out of the screen (i.e. not clipped), the likelihood is that bad data will be written to the memory, thus the reason for the clipping.
Logical Structure:
The basic hardware structure of our system is as follows: there are two MCUs, wired together over a common data bus, created by wiring I/O ports together between the 2 MCUs (in this case, Port A). One MCU is mounted on an STK500 board, and the other is placed on a custom PCB. The interconnection between the two is wired together via a whiteboard between them. The whiteboard also connects to the TV, through the A/V inputs. The slave MCU handles read from an SNES controller, and does direct digital synthesis to the TV, allowing for sound. The slave communicates over the bus with the master, which handles game logic, rasterization, and output to the TV.
The basic structure of our software system is as follows: the MCU opens with a title screen, loaded from flash. A second MCU interprets data from the SNES controller, and communicates with the master. Based upon input from the SNES controller, the master starts the game, and does various transforms of the objects on screen. The player can fire projectiles which then move on screen on a given orientation. The object(s) have coordinates, and they collision detect with the player, and the player's bullets.
Game mechanics:
Based upon the start input the master starts up the game, and gameplay begins. There is a randomly generated target that appears around the player tank, and the player tank can "shoot" the target to gain points, as well as a small ammo replenishment. The target is randomly respawned, and may move slightly. The player loses when they run out of ammo, and cannot ro solve that problem, as any inconsistency with the transform would appear as a distance error, rather than a fairly obvious resizing error.eplenish it by destroying the targets. The game then boots back to the title screen.
Hardware/Software Tradeoffs:
There were a variety of software and hardware tradeoffs that had to be made. The unfortunate circumstance is that we had to sacrifice much of our original vision for the game, as the MCU was simply not able to handle the video processing burdens we placed upon it. As well, our relative inexperience with graphics, as well as microcontroller hardware caused us to scale things back significantly. Initially, we had the problem of limited memory, which did not allow for any large number of verticies to be placed onto the screen at one point. We circumvented this problem by instead storing a base point vertex for each of the objects, and generating verticies through offsets from the base point, subject to the "orientation" of the object in the space we were looking at. This, however, placed a larger computational burden on the MCU, inducing flicker. We solved this problem by scaling down the raster as in Bruce Land's code, allowing for a larger amount of time to produce the necessary results. Unfortunately, even scaling down the raster would not allow us enough time to complete actual raster generation for complex scenes, even if raster generation were the only operation we performed between a frame. The original battlezone designers circumvented this timing constraint by having a specialized hardware vector display unit, which we lack. Thus, to fulfill timing constraints, we generated the raster in it's own cycle period (the period between successive frames of video), and pulled as much computational burden as possible away from that cycle, in order to produce as many vectors as possible, as well as to allow for a more complex and interesting game experience.
In addition, we suffered from small errors with our sin/cosine tables, since we only expressed them in 8x8 fixed point. As we continued to perform the transforms, the initial implementation would deform and bend oddly. Moving to a set of fixed offsets from a base point helped to relieve the problem somewhat.
Standards, Patents, Copyrights, and Trademarks:
The primary standard of interest in this case is NTSC, which mandates a picture system of 525 lines per frame, interlaced, at a framerate of approximately 29.97 frames/sec. The original standard called for a 30 frames/sec signal, but in order to properly integrate a color subcarrier signal, the framerate was somewhat reduced.
Color is added by adding an appropriate sine signal to the video signal, which is then interpreted by the circuitry on the TV itself. The screen is actually refreshed at twice the framerate (~60 hz), but the entire screen is interlaced, thus reducing the actual framerate to ~30 frames/sec. Interlacing simply replaces bands of the screen on alternating lines, which, which fixes the perceived screen flicker by means of persistence of vision plus the CRT afterglow. The timing constraints are handled by the source code provided by Bruce Land, as well as the basic raster generation.
The second standard of interest is the SNES controller standard. The SNES is a fairly simple design, which consists of gap-closing switches which allow for a current flow, and a shift register which latches the data from the switches. There are 5 pins which are used, 2 are N/C. Besides power and ground, there are 3 pins which are of note - a latch pin, a clk pin, and a data pin. The latch pin is fairly self-explanatory - by pulsing a logic high pulse into the latch, the register in the SNES controller latches the data from the pins. After the latching occurs, the data outputs to the data pin, which changes based upon the clock signal into the SNES controller. The button data are output in the following order (by clk pulse), with active low the order of the day - B, Y, Select, Start, North, South, West, East, A, X, L, and R.
In terms of patents, copyrights, and trademarks, the game Battlezone is copyrighted by Atari. However, our design and code is built from scratch, and we believe that we do not infringe upon any copyrights, patents, or trademarks held by any parties, as our design differs signficantly from the original implementation, and in addition we do not plan to profit from this.
Program/Hardware Design
Note 1: All code (as well as comments on specific code) is included in the appendix, along with the schematics and other assorted useful things.
Note 2: The primary source for most of this code is Bruce Land, who provided the video generation code, as well as the fixed point multiply/divide.
Primary MCU:
The primary MCU is the meat of the project. The primary running code is contained in a while block in the main function. There are two distinct blocks in the main loop. The MCU waits for a signal from the second microcontroller. Based upon the input, it either starts up the game, or continues to process the title screen. Once start input is recieved, it begins processing the game. The logic runs a different set of operations every cycle, running on a 3 stage system which cycles endlessly, based upon a counter which is reset in cycle 3.
Cycle 1:
The first thing it does is load the previously drawn base point verticies into a buffer, which allows them to be erased when the raster is redrawn. If a button is pressed for a new bullet, the code is processed here. A bit is changed on a "enabled" unsigned char, which allows for the system to keep track of what is enabled - the system will not perform certain tasks if an object is not enabled. Secondly, the hardware detects d-pad movement, which will change the orientation of the camera. The base points of the various objects are changed based upon their valid status, their orientations are changed as well. All of these are stored in a buffer for objects to be written to the screen. Basic collision detection happen at this point, as well - the system detects whether the bullet collides with either the pyramid or the target, by finding the absolute offsets between the bullet-target and bullet-pyramid, and checking against a threshold. If the bullet hits the pyramid, the bullet is disabled - if the bullet hits the target, the target and the bullet are disabled, score is incremented, and a respawn flag for the target activates. The bullet and target are also subsequently erased from the minimap.
Cycle 2:
First, the system checks if there is collision between a valid target and the player, as well as the pyramid and the player, and if any collisions occur, the previous movements are rolled back into the buffered positions. Afterwards, the bullets are translated based upon their relative orientation to the player tank, and the bullets is checked to see if the bullet is within bounds, and if not, bullet is invalidated and erased. The minimap function is erased and redrawn in this cycle, with the positions calculated by dividing the objects player-relative positions through right shifts, and displaying as points on the minimap. The score and the ammo counter are then updated. After all of this, if the respawn flag is set, the target timer increments. Based upon the increments, the random numbers are calculated, and then on the final increment, the flag is reset, and the target is respawned at a random location relative to the player tank. Lastly, there is a small AI portion which calculates a random number, and moves the target slightly based upon the output.
Cycle 3:
The major sticking point of our design, the 3rd cycle is dedicated to the rasterization algorithms. The draw functions are called here to both erase the previous objects, and redraw the new ones. In addition, crosshairs and an artificial horizon line is drawn. The draw functions are self contained functions which draw a single object, based upon its base point, and calculate the offsets based upon the object's orientation. Within the line_draw3d function, we calculate whether the line is within the viewing plane (i.e. within the 90 degree cone of forward vision), and then if so, do perspective correction upon it. We then clip the lines based upon the constraints of the viewing window, and do not render those who have points outside. Once this is completed, we run the Bresenham algorithm to complete our work and draw/erase the screen.
After this, there is an additional check to see if ammo has expired - if so, it resets the game back to the title, and resets everything accordingly.
Second MCU (SNES Controller):
The primary function of the second MCU is to interface with the SNES controller, reading in the information of which buttons are pressed cyclically and transmitting that information to the first MCU. The SNES controller has three pins (in addition to a Vcc power pin, a ground pin, and two unused pins), two of which are inputs and one of which is an output. The SNES is read by setting the latch input high, then after some time setting the latch low, then finally alternating between low and high clock inputs. After the first positive edge of the latch input, the data output is set to whether the B button is pressed. Then, after each positive edge of the clock input, the data output is set to, in order, whether the Y, Select, Start, North, South, West, East, A, X, L, or R button is pressed. By reading in the data output at appropriate intervals (between the positive edge and the next positive edge of the clock), the entire SNES controller can be read. In our implementation, the output is stored in a 16-bit int variable. The interval between triggering the clock is set to four nops (4*62.5ns for our 16MHz MCU), in addition to time used to update variables and branch (adding a few hundred more nanoseconds). Since two clock triggers are needed to read a button (trigger clock low then back high), around 24 aforementioned intervals are required to read the entire 12 buttons of the SNES controller. Thus, it takes approximately tens of microseconds to read the entire SNES controller. Our design reads the SNES controller every 10ms, driven by a timer, and outputs the result to pins 2 through 7 of Port A of the MCU. Since we assign a button to a pin (if we encode the button into smaller number of bits, we can’t discern multiple buttons being pressed simultaneously), we only transmit the information for 6 buttons – the four direction buttons, A, and X. These buttons are sufficient to control our game.
Second MCU (Sound Generation):
Another function of the second MCU is to output audio to the TV based on cues from the first MCU. We decided to use the remaining pins 0 and 1 of Port A to receive audio commands from the first MCU. The audio generation scheme is the DPCM scheme, explained in great detail on Bruce Land’s speech generation page (see appendix). In this scheme, a sound sample is encoded into a sequence of 2-bit values, each value representing a difference in amplitude from the previous value. Hence, a sound signal could be reconstructed by starting from some amplitude value, and increasing or decreasing the amplitude over time based on the sequence of 2-bit value read. This is performed by the MCU through the method of PWM (pulse width modulation). A base oscillating pulse is output, and the width of the pulse is dynamically adjusted based on the sequence of 2-bit values discussed above. Thus, a speech signal is encoded into a higher frequency oscillating pulse signal. A simple capacitor-resistor low pass filter with cutoff frequency of ~3121 hz is used to attenuate/eliminate the high frequency pulse signal.
Since we only have 2 pins to receive in audio commands from the first MCU, only four different commands can be differentiated: 00, 01, 10, and 11. We read commands at the same frequency as reading the SNES controller: once every 10ms. We let 00 be the “ready state” command; when the MCU sees this command, it enters a “ready state” where it starts playing a sound when another command is entered on a future cycle. While it waits, it finishes playing any sounds it had been playing when it received the command. Commands 01 and 10 are, respectively, the “incoming” and “target neutralized” commands. When either command is seen, the MCU starts to recite the name of the command, if the same command was not seen in the previous cycle. This is to prevent the MCU from repeatedly starting over when trying to recite a speech when it encounters a command that is maintained for extended periods of time. Finally, command 11 is the “silence” command, which stops any speech currently being recited. This command is functional, but is not used in the implementation of the game.
Hardware:
The hardware design for this system is relatively simple. We wired up PORTA on both microcontrollers together to act as a data bus. We wired up PORTB on the custom PCB to read data from the SNES controller, connecting power, ground, and 3 pins to act as clock, latch, and an input for data.
Things we found hard:
Clipping the objects to only render in the forward area was somewhat of a challenge. We initially clipped the line draw to only function in areas where z > 0, but that proved to be useless against the items that were outside of the view cone with positive z (although our objects did not typically fall into that range, they occasionally did, which caused serious frustration until we compared Z with the absolute value of X, where we did not render objects that fell outside of the cone |x|< Z.
Also, cutting down the number of cycles was difficult, as we needed more time for proper calculation. Other than shifting the burden to other frame cycles, it was nearly impossible to render without significant flicker. More efficient algorithms would most definitely be helpful in this regard. Someone with assembly skills could likely capitalize on the speed gains offered.
Additionally, the memory constraints were hard. They were a force that was difficult to fight against without some sacrifices - i.e. cycles, loss of detail, etc. Addition of an SRAM chip would be useful in this regard, but timing and signal generation would be a potential issue. One potential approach we used was to use offsets to generate the verticies, and then store the x,y coordinates after transform in an array. This allowed us to do the division (which was slow) before hand, and sped up the draw process. However, constraints on the divisions must be tight, otherwise division by zero could cause the algorithm to stall - something that tripped us up occasionally.
Things which did not work:
We attempted to implement an SPI system, but were unable to get synchronous data transfer between the two microcontrollers. Our initial plan was to try and generate raster on one MCU, and display on the other, but then we realized that we would still be subject to the same time constraints, only perhaps a little better, and ended up abandoning the idea. Our initial concept was to have one MCU generate raster, and the other display it, but we realized that would not help the timing constraints between the two systems. A different mechanism of sharing data and processing the raster will be necessary for optimum performance.
We were never able to get the perspective corrected box to work correctly - we believe that the proportions/perspective correction was not quite the same as battlezone, and thus the box appeared strange. It may have something to do with the way we perspective corrected the X coordinates, as the original game appeared to have less of an X-based offset and a larger bias on the Y-based offset.
We also tried interrupt decoupling, but that resulted in dropped frames, which is unacceptable for the implementation we were trying for.
Results
We were able to get a flicker-free signal from the TV, although it did indeed have to be downscaled, as well as updated only every 3 cycles (i.e. 10 updates per second). We were able to render a basic 3d world, with a horizon line, pyramid obstruction, and a slowly moving target. The controller is usable, with correct input to the TV, and the sound generation, controller data gathering, and the video processing running concurrently. In terms of accuracy, the distances deviate considerably with repeated rotations/translation, as the cosine and sine terms we use are rather imperfect reflections of the actual terms. We were able to get correct perspective transformed targets, as well as perspective corrected pyramids. There are still cycles leftover, which more items could be represented in. However, we did not want to overtax the system - we tried to keep it simple, and polish what we have into excellent shape, and made sure it ran well.
In terms of safety, there is still a possibility that photosensitive people would be caused harm by the rapidly changing screen, but we made a conscious attempt to reduce flicker and odd signals such that any risks would be reduced. Otherwise, the project is fairly harmless, unless you spend too much time playing it and waste away and die, etc.
Our design is usable, and designed as both a proof of concept (that a 3d game of any sort can run in real-time on an ATmega), as well as a useful stepping stone for those who wish to perhaps follow down a similar path. In terms of playability, the game itself is very playable, with the majority of the game dynamics fleshed out and extensively tested (AI and object wraparound is still basic, and could be improved.)
Conclusions
Expectations:
We would have to say that the outcome of this project met our expectations, although it is a little disappointing that we had to scale the game back significantly in order for us to get something that was both useable, smooth, and playable. We take into consideration that the original Battlezone took nearly a year of development, as well as specialized hardware to run, and thus we are happy that we have made at least some inroads towards it. Also, it was done by a team of highly trained hardware as well as software engineers who had knowledge of the system they were working with. Neither of us had previous computer graphics experience, nor did we have previous microcontroller experience outside of 476. That we could accomplish anything like this in the short span of a month is quite something in itself.
There is definitely a lot of optimization that can be done that would improve performance, but there's still the heart of the problem that a maximum number of pixels can be reasonably drawn per frame, and hopefully someone more hardware-oriented (or microcontroller-oriented) will be able to find a useful solution that could circumvent the problem.
Standards:
We obeyed all standards placed upon us, and did not deviate from them in any way, shape, or form. The NTSC standard was already implemented, and the SNES standard was trivial to implement.
IP concerns:
The major contributor to our project is Bruce Land, and we make signficant reference to him on this website. We used his code as the base code, and added our own personal contributions. Besides Bruce's code, we used no other person's code, no samples, and there is no patent opportunity (as Battlezone is already trademarked). The only thing we really used from others would be the speech samples provided by the AT&T website as a demo of their speech generation capabilities, but otherwise no other sources were really used.
Ethical Considerations:
It is our belief that ethical considerations should be of high concern for engineers, and throughout the project have strictly followed the IEEE code of ethics. Our design is a video game, and hence flickering is an important consideration for users with photosensitivity and epilepsy. We have put great effort into eliminating flickering in our design, and tested the design thoroughly to ascertain no flickering occurs. However, we are unable to guarantee that no flickering occurs under all conditions, and hence ask photosensitive users to take proper precautions when operating our device.
The claims made and the operation described in this web page are correct and honest to the best of our knowledge. The project was completed in its entirety without the involvement of bribery, discrimination, or malicious intent of any kind toward any person. We have listened to and considered any suggestions or criticisms toward our project offered by course teaching assistants, fellow classmates, and Professor Bruce Land. It is our goal that through this project, we have enriched our technical understanding and competence. We believe we have achieved that goal.
Legal Considerations:
Our design does not use any RF transmitters, and hence we are not in violation of any FCC standards concerning RF transmission. We adhere to NTSC standard, and do not do anything weird with the TV signal or audio generation. While our game is based on a commercial game by Atari, we have built our design and code from scratch, and believe that we are not in violation of any copyright laws, as we did not reverse engineer anyone's code, nor did we really use the original game as anything more than a vague inspiration.
Acknowledgements:
We also acknowledge those who have put forth their time and effort to help us, and thank them for their contribution to this project, especially Bruce Land, for a great course, a great year, and his excellent help with the majority of our project. We would also like to thank the TAs, specifically Adrian Wong, who has provided both his help and support, even when his M.Eng work has pounded him into the ground.
Appendix
Program Listing:
btank.c - our humble contribution to the cause of Atmega32 based 3d gaming
flashstuff.h - title screen, as well as flag animation
secondmcu.c - the sound generation and SNES control from the second MCU
dpcmtable.h - the sound files generated by the second mcu
Schematic:
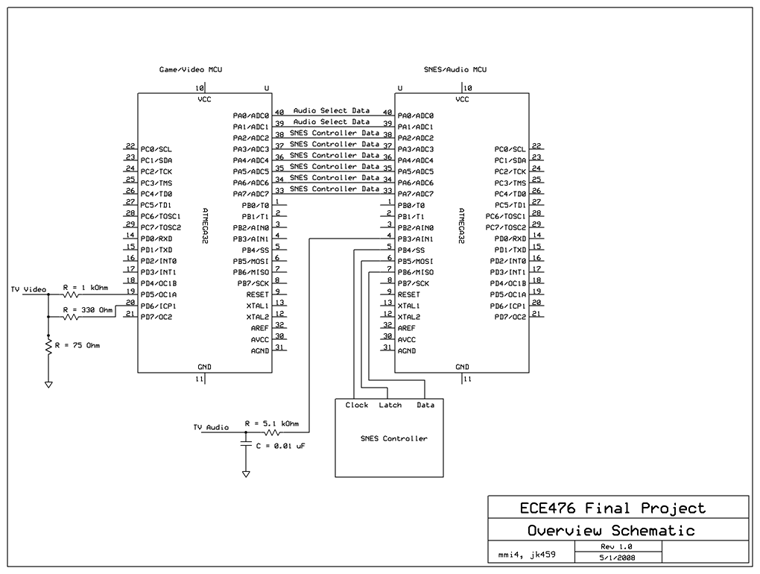
Cost Breakdown:
Total cost: $63.90
Task Breakdown:
Matt -
Jsoon -
References:
NTSC video generation guide by Bruce Land
Speech Generation Guide by Bruce Land
Rogers, David F. Procedural Elements for Computer Graphics. McGraw-Hill, 1985.
Us:
