16-bit floating point

Cornell University ECE4760
Floating Point Arithmetic
Pi Pico RP2040

Floating point on RP2040
There is full support in the ROM for IEEE 32-bit floating point (fp32). What we are attempting to do here is to see if 16-bit floating formats have useful range and resolution, but faster execution. For speed comparision, a fixed point format, s15x16 is included.

The system implemented is 16-bit floating point (fp16), with similar bit layout to the IEEE standard FP16, but without infinities or NANs, or denorms. The reason for doing this annoying exercise is to see if the Lattice-Boltzmann solver runs better in limited precision, and therefore faster, floating point than in fixed point. The 16-bit floats have a dynamic range of 1e5 and resolution of 1e-4. The bit layout is
[sign 1-bit | exponent 5-bits | mantissa 11-bits (10-bits actually stored)]
Sign is one for negative. The exponent is in offset binary. The maximum exponent, 2¹⁵, is 0b11111, and the minimum, 2^-15, is 0b00000. Since there are no denorms, the most significant bit of the mantissa does not need to be stored, since it is always one. The mantissa is therefore a value between 1 and 2, with 10-bit resolution. We implemented:

add/subtract
multiply
divide
inverse sqrt
compare
shift -- This is an unusual float operator equvalent to mult/div by powers of two
negate
absolute value
integer <> fp16 and IEEE <> fp16

A version called fp16V allows you to change the exponent bias to shift the range of the 16-bit floats to +/-2, with a resolution of 1e-9. The exponent is in offset binary, and in this case he maximum exponent, 2⁰, is 0b11111, and the minimum, 2^-31, is 0b00000.

For comparision to fp16V, the s15x16 format gives good dynamic range for animation and high accuracy for fast cutoff IIR filters. The format s15x16 means 16 bits to the left of the binary-point, one of which is the sign bit. The range is +32767.9999 to -32768.0 and the is resolution 2^-16=1.5e-5. The range is enough for addressing pixels on a VGA screen, for example, and not worry too much about overflow.

Execution speeds
Execution speeds are estimates because the execution path through floating routines, particularly floating add, is variable. Fp32 and fp16 addition have about the same execution speed, while s15x16 is ten times faster. Fp16 and s15x16 have about the same multiply speed, and are about three times faster than fp32. When used in an actual ODE solver, the fp16 and standard fp32 were the same speed and s15x16 was around a factor of 8 faster. For speed, fixed point is the clear winner. If memory footprint matters more than speed, then fp16 may have the advantage.

Floating Inverse-square-root (isqrt)
There is a weird, bit-twiddle, trick that will extract the isqrt of numbers in fp32 or fp16 format. It is explained in https://en.wikipedia.org/wiki/Fast_inverse_square_root. The summary is that a number stored in fp32 or fp16 format is a reasonable approximation of the log of the number. Therefore, shifting it right by one bit makes it an approximation of the log of the square-root. Subtracting it from a constant inverts the log, while the constant does a bit more correction to the estimate. Treating the literal bits of the fp16 as an integer i,
i = 22971 - ( i >> 1 )
gives an estimate of the log of the isqrt. Storing this again as a fp16 and running one Newton interation to refine the estimate is the final isqrt. The 'magic number' 22971 is
1.5 * 2^(num_mantissa_bits) * ((exp_offset)-0.045)
For fp16; exp offset = 15 ; num mantissa bits = 10
See particularly the section "First approximation of the result" in the Wikipedia article.

FP16 code: this just the raw speed and correctness tests.
C code, cmakelist, ZIP of all files

Heun (second order, explicit) ODE solver for a sine wave oscillator.
To test in a real numerical applicaiton I coded up a solver for a spring-mass system. This was chosen because an analytical solution (example) is easy to get for comparision to the numerical solutions. A linear, second-order differential equation resulting from a damped spring-mass system:
d²x/dt² = -k/m*x-d/m*(dx/dt)
where k is the spring constant, d the damping coefficient, m the mass, and x the displacement. We will simulate this by converting the second-order system into a coupled first-order system. If we let v1=x and v2=dx/dt then the second order equation is equivalent to (where f1 and f2 are used below in the Heun method outline):
dv1/dt = f1 = v2
dv2/dt = f2 = -k/m*v1-d/m*v2
We can then use fp16, fp32 and s15x16 arithmetic systems to write the Heun method:

    Form the slope kv1, kv2 for each variable at time=n
    kv1 = f1(v1(n), v2(n))
    kv2 = f2(v1(n), v2(n))
    Estimate one step forward for each variable
    v1t = v1 + dt*kv1
    v2t = v2 + dt*kv2
    Form the slope mv1, mv2 for each variable at time=n+1
    mv1 = f1(v1t, v2t)
    mv2 = f2(v1t, v2t)
    Average the two slope estimates and advance one step to get the new values of v1 and v2.
    v1(n+1) = v1(n) + dt*(kv1 + mv1)/2
    v2(n+1) = v2(n) + dt*(kv2 + mv2)/2

This scheme is technically a second-order, explicit, self-starting, predictor/corrector method.
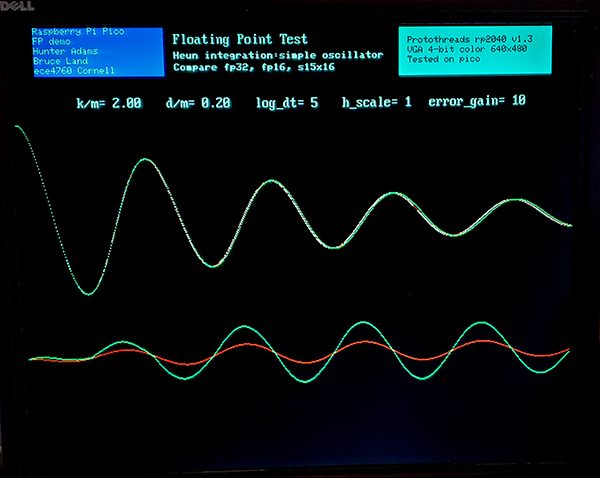
It produces an estimate of the time course of v1 and v2. A plot of V1 is shown below in the top trace below. All three solvers essentially overlap. The bottom traces are the errors (x10 vertical gain) for each solver. The fp32 and s15x16 are overlapped in the blue trace. The green fp16 trace has noticably more error, but still probably good enough for video games. This was true over a large range of system parameters. Probably the truncation of add/subtract to 11 bits is an accuracy killer. The error amplitude for the fp32 scales as the square of the step size, as expected for a second order method. At the shown step size of 1/32, the error for fp32 and s15x16 are both around 0.002 of the solution amplitude. The error for fp16 is around 0.02. The error for all three arithmetic systems increased for lower damping or higher frequency.

Code
Project ZIP