ECE 4760: Laboratory 3

Video Game -- Particle Beam

You will produce a game in which ball-like particles enter from one side of the screen. You must deflect the balls with a paddle (while conserving momentum) to keep them from hitting your side of the screen. The paddle will be controlled by an analog input. There will be a time limit to the game. Display will be on a TV, with sound effects. The balls will follow standard billards-type dynamics, with zero friction between balls. An example of billard dynamics is shown here and slower.

You will probably want to review the code examples given in Video Generation with AVR.
Use this example as a basis for your program. You must uncomment the multfix routine or put multASM.S in the project source.

Build the video DAC shown below and connect it to the yellow connector on the LCD TV using clip leads and a RCA phone jack.
Note that you should remove the jumpers connecting D0 and D1 to the USB chip, circled below.

The game will be controlled by a potentiometer hooked to an A/D input on the MCU. Use the circuit to the left to make a user-variable voltage. I suggest setting Vref to Vcc on the A/D converter. This example (ADCtestGCC644.c uart.c, uart.h, project zip) shows how to set up the A/D converter to read a trimpot.

Dynamics

You are going to be programming in the equations of motion for the balls. Remember that the video coordinate system has x increasing to the right and y increasing downward. We will step the billards system forward in time by calculating the total change in velocity from a collision, without worrying exactly how forces change the velocity.

The change in velocity during impact can be derived for frictionless balls of equal mass by noting that the the impact force must act in a direction parallel to the line connecting the centers of the two impacting balls. The change in velocity must be parallel to the connecting line also, with the velocity component parallel to the line having its sign reversed by the collision and the velocity component perpendicular to the line unchanged. Projecting the initial velocity onto the line connecting the centers, negating the result, and resolving it back into x and y velocity components gives the velocity change. If i and j are the indices of the colliding balls, define:

then delta v for ball i is given by the following where the right-most term represents the projection of the velocity onto the line and the other term converts the projection back to x,y coordinates.

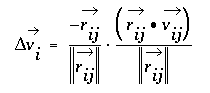
The calculation procedure for each time step is:

1. Compute the Δv for each collision, based on the positions of the balls, and add it to the current velocity. Do this for every pair of balls. This step is time consuming, but only has to be performed for any two balls if they are less than 2 radii apart. Ball-ball collisions will not be exact because of finite time steps. One consequence of this is that balls tend to capture each other when they collide. You will need to do a numerical hack to avoid capture. I suggest that after a ball collides with another ball or the paddle, that it not be allowed to collide again for a few frames.
   Pseudocode for this might be:
   For each ball i from 1 to n
  For each ball j from i+1 to n
    Compute rij
    if (||rij|| less than 2*(ballRadius) and hitCounter is zero)
      Compute vij
      Compute Δvi
      Add Δvi to vi
      Subtract Δvi from vj
      Set hitCounter big enough to avoid particle capture
    elseif (hitCounter>0)
      decrement hitCounter
    endif
  end
end
When I coded this, I did not bother to calculate the square root of the sum of squares when calculating ||rij|| (too slow). Instead, in the if statement, I just used the approximation that to be within hit range, the absolute value each component of rij was less than 2*ballRadius. When dividing by ||rij||² you can use the known value of (2*ballRadius)2. In the assignment below, I set ballRadius=2.
2. For each ball, simulate friction between the ball and table by making
   vx(t+dt)=vx(t)-vx*drag and vy(t+dt)=vy-vy*drag
The drag should be small, perhaps drag=0x0001 (in fixed notation).
3. Update the positions according to
   x(t+dt)=x(t)+vx*dt and y(t+dt)=y(t)+vy*dt
4. Detect collisions with the walls and modify velocities by negating the velocity component perprendicular to the wall.
5. Delete any balls which hit the left wall or "catch bins".

Clearly, v and x all need initial conditions, which you will set, according the specifications below. It is doubtful that you will have enough time between frames to do all of the calculations in floating point. I suggest using 16 bit, signed numbers with the binary point set at the byte boundary. I also suggest scaling velocity so that you can make dt=1, thereby avoiding a multiply. There is an example of a bouncing ball with drag done with fixed point numbers.

The previous analysis is adapted from: Studies in Molecular Dynamics. I. General Method, by B. Alder and T. Wainwright, Journal of Chemical Physics, Vol 31 #2, Aug 1959, pp 459-466. See also Hard-Sphere molecular dynamics. One final project in 2005 used a different scheme to calculate collisions.

You will need your digital camera to document your project.

Results:

2011: video
2014: video Shiva Rajagopal and Richard Quan

Write a program in C and possibly assembler for the microcontroller with these specifications:

• At reset, the program should:
  • draw a playing field consiting of a rectangle 128 widex 64 high on the TV screen. You can gain a lot of computation time if you modify the video code to only draw the required number of video lines.
  • set the running time clock to zero. The clock should read elapsed play time.
  • start firing balls of radius 2 pixels onto the right hand edge of the screen with v_x=-30 to -60 pixels/sec and v_y=+5 to -5 pixels/sec. You can vary this to make the game more playable, if necessary. The ball icons can be very simple.
  • draw a "paddle" consisting of a sphere with a radius about 5 times the size of the balls. You can vary this to make the game more playable, or to produce harder levels of play.
• At each frame (or group of frames), update the velocity and position of all the balls on the screen, and redraw the paddle. The drawing of the paddle need not be complicated.
• Balls which are deflected into a "catch bins" increment your score, and the balls are removed from the screen. Balls which reach the left side of the screen decrement your score, and are removed from the screen. The catch bins should be holes in the top and bottom line of the rectangle. You can adjust the size to make it playable.
• A score and time should be displayed.
• All balls can be deflected by other balls according to the hard ball dynamics given above. Ball interaction with the paddle follows the same dynamics.
• Paddle vertical position on the screen should be changed by a potientiometer attached to the A/D converter. The paddle horizontal position will be fixed at around x=6.
• The game ends after a fixed time, which you can choose.
• New balls should enter the playing field at regular intervals (from the right hand edge), perhaps twice per second. The oldest ball will be removed from the screen. If the ball has not hit the left hand wall by the time it is removed, your score is incremented.
• You will be graded on the number of simultaneous balls you can animate. You must animate at least 10 balls. You will need to optmize your code, split computations across up to three frames, and perhaps convert some code to assembler. Notice that the number of computations of ball collisions increases as the square of the number of balls.
• There should be no video artifacts (rolling, tearing, flickering) during operation.

When you demonstrate the program to a staff member, you should play the game.

Your written lab report should include the sections mentioned in the policy page, and :

• The scheme you used to coordinate video and the ADC.
• The details of your integration algorithm.
• An image from the TV (bring your camera).
• A heavily commented listing of your code.