Cornell University
BioNB 441
Using Images

Introduction.

Images and image analysis has a large role in neurobiology including:

Matlab makes it easy to produce and handle images algorithmically. It fills a different niche from a program like Adobe Photoshop which allows human artistic interaction with an image. You might use Matlab image abilities to process a few hundred microscope images in order to filter, convert to grayscale, and store as a movie. Such a process would be very tedious using an program designed for artistic manipulations.

The examples will use Matlab and the Matlab Image toolbox.

Examples

  1. Moving sinewave grating images are often used as simple visual stimuli. The following program generates a vertical grating, stores it as a movie, then plays it back several times. 
    clf
clear all
set(gcf,'doublebuffer','on');

%Build the grid which determines the image resolution
[x,y] = meshgrid(1:256,1:128);

%initialize the movie
n=40;
mov=moviein(n);

%build the frames
speed=.05;freq=.2;
for i=1:n
   %the frame is just a sinewave grating
   %intensity modulated to--to-botton
   img=128 * (sin(x*freq+speed*i)+1) .* y.^2/128^2;
   image(img);
   %add a frame number
   text(10,10,num2str(i),'color','white')
   %Force real pixels
   truesize(gcf)
   %transfer the image to a movie frame
   mov(i)=getframe; 
end

%clear the image
image(0*x);axis image;
pause(1);
%playback the movie 
%--five times, with reversal
%--at 30 frames/sec
movie(mov,-5,30);
image(0*x);axis image;
    One frame from the animation is shown below.

  2. We can use signal processing techniques to produce an image of a fractal coastline. A random 2D array of complex frequencies is constructed, then filtered by multiplying by a power law of 1/fc. The flitered array of complex frequencies is then transformed back to a space-array, and added to a bias function to make an island or a lake. The array of altitudes is then turned into an rgb image and displayed. 
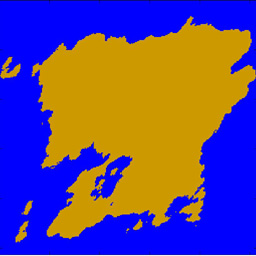
    % generate a fractal coastline via FFT
clf;
clear all;

%grid size
n = 256;
[x,y] = meshgrid(1:n,1:n);

%Generate a random frequency domain grid
s = sum(100*clock);
rand('seed',s);
freq = (rand(n,n)-.5) + i* (rand(n,n)-.5);  
% Set the DC level to zero
freq(1,1) = 0;	 

% Slope of cutoff filter in freq domain
%less negative => rougher outline 
%-1.5 to -2.5 is reasonable for real coestlines
c = -2.1; 
%
% make a matrix with entries proportional to the freq
dist = sqrt( x.^2 + y.^2 ) ;

% Reduce high freq components by a power law f**c
%to make a fractal surface
filtered = freq .* dist .^c ;
surface = ( real(ifft2(filtered)) ) ; 

%add a bias to make a lake or a mountain
%just change the sign when adding the bias to the surface
bias = 6e-8*sqrt( (x-n/2).^2 + (y-n/2).^2 );
bias = bias-mean(mean(bias));
surface = surface - bias ;

%Convert to a rgb (truecolor) image
surface = cat(3,...
   .8*(surface>0), ...
   .6*(surface>0),...
   surface<=0);

image(surface);
truesize(gcf);
    An example is shown below.

  3. Another signal processing application is generating band-limited, random, moving visual noise to use as a background for visual stimuli. An example animation shows an image bandlimited in time to about 5 frames and bandlimited in space to about 2-10 cycles. The program generates random complex numbers as a basis for moving Fourier synthesised patterns. 
    figure(1)
clf;
set(gcf,'doublebuffer','on')
clear all;

%grid size
n = 128;

%Generate a random frequency domain grid
s = sum(100*clock);
rand('seed',s);
freq = (rand(n,n)-.5) + i* (rand(n,n)-.5);  
%Set the DC level to zero
newfreq(n/2,n/2) = 0;

%low pass parameter--bigger means faster pattern
alpha = .1;
%lowest spatial frequency -- units are cycles/frame width
lowcut = 2;
%highest spatial frequency
hicut = 10;
 
% make a matrix with entries proportional to the freq
%for use in filtering in freq domain
[x,y] = meshgrid(1:n,1:n);
dist = sqrt( (x-n/2).^2 + (y-n/2).^2 ) ;
    
for j=1:120
    %get the next random input
    newfreq = (rand(n,n)-.5) + i* (rand(n,n)-.5);  
    % Set the DC level to zero
    newfreq(n/2,n/2) = 0;	 
    %lowpass filter combines old and new state
    freq = freq *(1-alpha) + newfreq*alpha;
    
    %band-pass filter the spatial frequency
    filtered = freq .* ( (dist>=lowcut) & (dist<=hicut) );
    
    %make the intensity distribution
    surface = abs( (ifft2(fftshift(filtered))) ) ; 
    %and scale it to 0-1 range
    surface = (surface - min(min(surface)))/(max(max(surface)) - min(min(surface)));
    
    %Convert to a rgb (truecolor) image
    dis = cat(3,surface, surface, surface);
    %display the grayscale image
    imshow(dis);
    truesize(gcf);
    colormap(gray);
    mov(j) = getframe;
    %drawnow
end

figure(2)
movie(mov,1,30);
  4. This example uses binary images to compute the overlap of two regions. The regions represent the ranges of two different animal species computed as the convex hull of the positions in which animals are actually seen. The following program computes two animal distrbutions, then steps through the area analysis visually. 
    %make two animal distibutions
dist1x=randn(100,1);
dist1y=randn(100,1);
dist2x=randn(100,1)+2;
dist2y=randn(100,1);

%compute the convex hull of each
c1=convhull(dist1x,dist1y);
c2=convhull(dist2x,dist2y);

%plot the two distributions and 
%their respective convex hulls
figure(1)
clf
hold on
plot(dist1x,dist1y,'r.');
plot(dist1x(c1),dist1y(c1),'r');

plot(dist2x,dist2y,'b.');
plot(dist2x(c2),dist2y(c2),'b');

%will need the image size below
xdist=get(gca,'xlim');
ydist=get(gca,'ylim');

%=============
%fill the convex hull polygons
%convert them to binary images
%then compute the intersection area
%and compute the area ratios

figure(2)
clf
hold off
axis image
fill(dist1x(c1),dist1y(c1),'r');
set(gca,'xlim',xdist);
set(gca,'ylim',ydist);
pause(1)

img=getframe;
d1bw=~im2bw(img.cdata,.9);
imshow (d1bw);
pause(1)

fill(dist2x(c2),dist2y(c2),'r');
set(gca,'xlim',xdist);
set(gca,'ylim',ydist);
img=getframe;

d2bw=~im2bw(img.cdata,.9);
imshow (d2bw);
pause(1)

%trim the image edges because of 
%bogus pixels at the edges
[a b]=size(d1bw)
d1bw=(d1bw(5:a-10,5:b-10));
d2bw=(d2bw(5:a-10,5:b-10));

imshow(d2bw & d1bw)

disp('areas')
bwarea(d2bw & d1bw)
bwarea(d2bw & d1bw)/bwarea(d2bw)
bwarea(d2bw & d1bw)/bwarea(d1bw)
    An example of two disributions and their computed overlap region is shown below.