Introduction
Our project attempts to model the random process of an evolution using how well the organism plays the classic game of Tic-Tac-Toe as a fitness function with the end goal to create the perfect Tic-Tac-Toe machine.
Evolutionary algorthms can solve complex problems that may not be able to be solved in traditional analytical or numerical methods by using random chance to find a local maximum in a fitness function. Tic-Tac-Toe is a good example of this kind of a problem because games tend to have strategies buried behind massive amounts of data, in this case, thousands of boards and hundreds of thousands of possible paths through them [1]. The aim of this project was to explore evolutionary algorithms on an FPGA using how well an organism plays the game of Tic-Tac-Toe as a fitness function.
High Level Design
Rationale and Sources of our Project Idea
Machine learning algorithms have extensively been applied to solve simple games such as tic-tac-toe, checkers, go etc. Machine Learning essentially involves analyzing large amounts of data to find patterns or knowing the constraints of a problem beforehand. The idea behind using evolution to make an ideal tic-tac-toe player was to remove human cognition from the process of a creating a player. This method is in inspired by Darwin's theory of evolution. Just like in nature, the algorithm goes through multiple generations or organisms (that play games of tic-tac-toe). The population of each generation is a set of potential solutions and the organism that has a good solution, i.e. the best fit in the current population, is used to produce the population of the next generation of organisms. In this manner new potential solutions are created. After an certain number of generations average fitness begins to approach maximum fitness, ultimately producing a population of organisms that have the best solution to the problem.
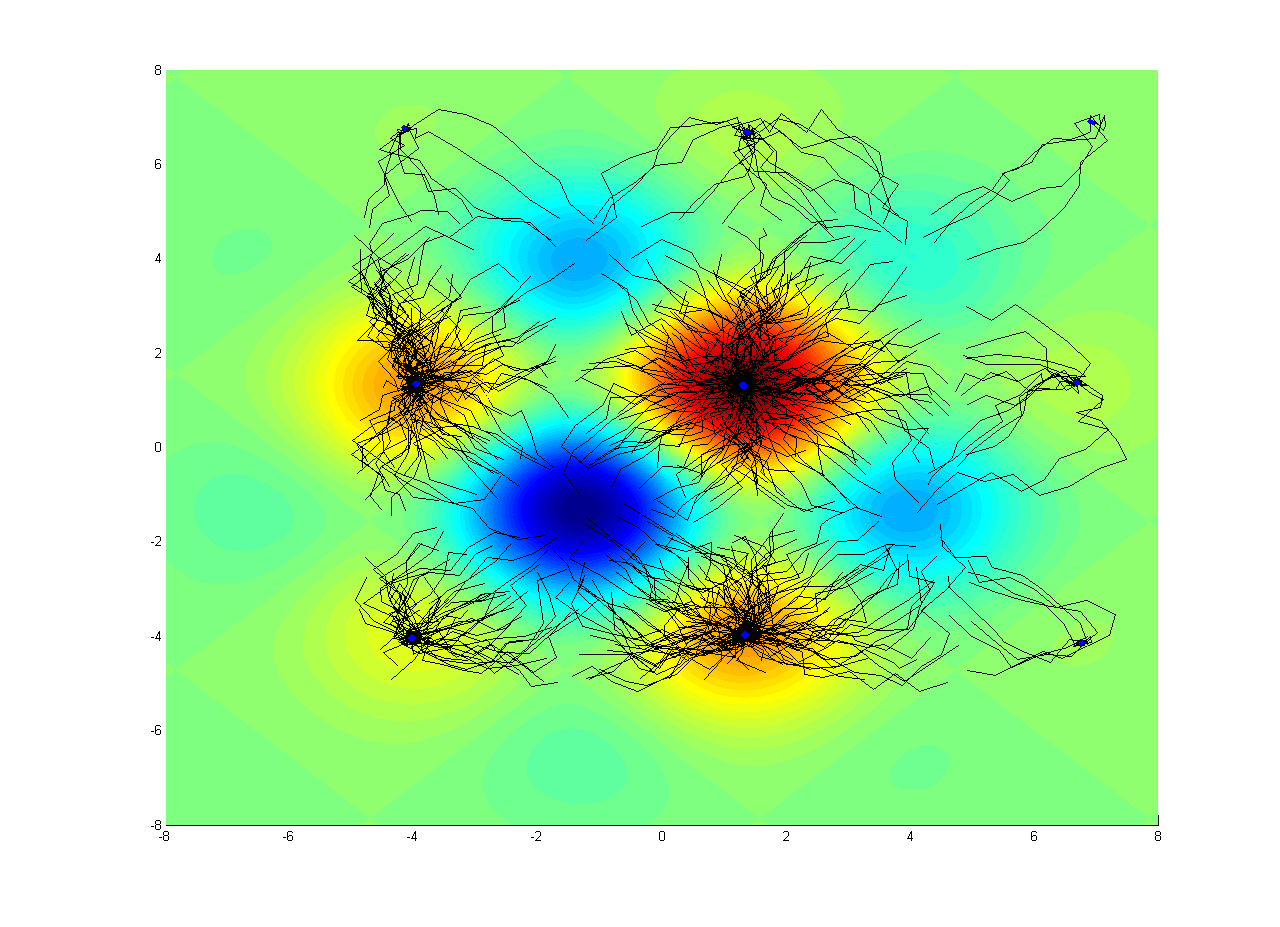
The figure above shows a perfect example of how evolutionary algorithms can be used to find local maxima. The black lines are seen converging to points where the algorithm guesses are local maxima indicated by blue dots.
Logical Structure
The simplicity of tic-tac-toe lies in the fact that, it is a two person zero sum game and each game has a definite outcome. Also, all possible board layouts that can be reached and all possible games that can be played, can be determined. In theory there are 362,880 (ie. 9!) different sequences for placing the Xs and Os on the board; that is, without taking into consideration winning combinations which would make many of them unreachable in an actual game; Conditions for feasibility of a board are :
- Assuming X moves first, the number of X's in a board is always equal to or one more than the number of O's in the board.
- A player does not make a move in case the other player wins.
Representing a Strategy and a Solution
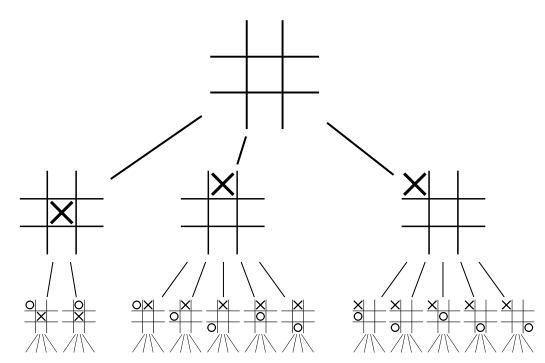

A move is represented by a branch in the tree, and the path through the whole tree is a "strategy" towards completion (regardless of a victory, loss or a draw)
When winning combinations are considered, there are 255,168 possible games. Assuming that X makes the first move every time:
* 131,184 finished games are won by (X)
* 77,904 finished games are won by (O)
* 46,080 finished games are drawn
The idea here is to evolve no-loss strategies i.e. paths through the tree that lead towards a win or a draw, as either player.
Initialization of the Population
We begin with 100 players; each player has 3^9 array indices, the array index itself corresponding to a unique board setup. Each array index contains an integer between 0 and 8 corresponding to a move on the board. The array is initialized with random numbers between 0 and 8, for the first generation.
Gameplay
Each player plays a game against every other player, making a total of 198 games per player per generation (99 as X and 99 as O). The algorithm takes a move, plugs that into the board and passes the new array index (i.e. the board setup) consequent to that particular move. The other player uses this index to determine the next move, which is located at that particular index in the array. The play proceeds until a winning board is reached, the board is filled or an invalid move is made. W win or a draw in yields 0 points and a loss yields a -1.
Fitness Evaluation
The scores from each game are totaled, giving us the total score for each player in each generation. The fitness function is the score, the highest score being the best fit.
Evolution
The genes here are the values stored in the player array and the organisms evolve through 2 distinct operations: selection and mutation.
- selection: Keeping the algorithm in contention with Darwin's theory of evolution, the best fit from a generation is chosen as the singular parent for the whole next generation. This makes reproduction essentially unicellular and every other organism (i.e. ones that are not the best fit from the current generation) is 'killed', i.e. their genes are not passed on. The best fit is determined by the fitness function, which is detailed above.
- mutation: Again, keeping the laws of nature in mind, it is not necessary that the genes from the parent are replicated exactly in the offspring. Random mutations might occur that cause offsprings to have genes slightly different from the ones in the parent. In this algorithm we have assumed a static 2.5% chance that a mutation might occur while passing the genes from the parent to the offspring between two successive generations.
Program/Hardware Design
Program Details
board[9] -
Used as the start board in each game, initialized to all zeroes, indicating a blank board.
organism[i][j] -
The actual player population; 'i' indicates the player number and 'j' indicates the gene.
randomize -
Initializes the population with random values between 0 and 8.
winningplayer -
Performs the first operation, i.e. selection and also generates the statistics for each generation such as Worst player, best player and individual player scores.
compete2 -
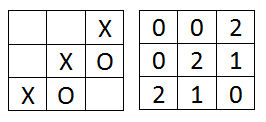
For games between two computer players, the game starts with a blank board, i.e. all values are zeroes. X's are represented by 2's and O's are represented by 1's, hence blank slots on the board are represented by zeroes. ex: when X makes a move on the board the value stored in that location is a 2, or 1 if O makes a move. This is done only for simplicity of computation in the program, there is no particular significance to these assigned values to the evolutionary algorithm itself.
mutate: As the name suggests, this function performs the second operation necessary for evolution.
board2int -
Encodes a unique boardsetup to a unique integer value (between 0 and 19683), that is in turn used to index the player array.
int2board -
Decodes a integer from the player array index to a boardsetup, used only for diagnostic purposes.
boarddisp -
Displays the current board state, used when playing against a human player.
competeasx -
For the human player to play as X (the human player takes the first turn)
competeaso -
For the human player to play as O (the computer player takes the first turn)
Hardware Details
For simplicity of operation, and ease of writing code, we instantiated a NIOS-II processor and did all of the coding on the NIOS-II IDE and we only used the actual hardware on the board for human-computer gameplay.
Each switch in SW[8:0] correspond to a location on the tic-tac-toe board and turning the switch on makes the actual move.
SW[17] - Continue evolution when on.
SW[16] - Human plays as X when on, takes the first turn.
SW[15] - Human plays as O when on, computer takes the first turn.
Results of the Design
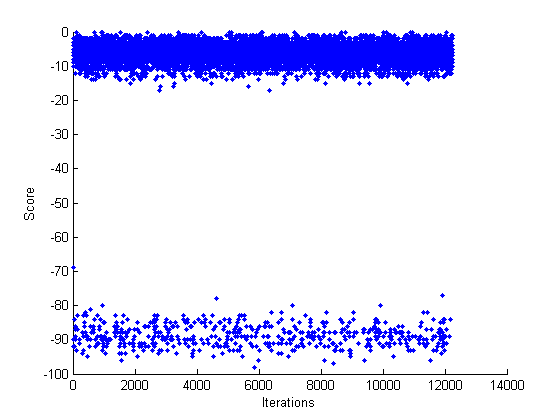
As of writing, the algorithm has gone through 12,542 iterations. There has been a measurable improvement in performance from the earlier iterations. Our program punishes invalid moves (moves that involve a player trying to make a move where there is already a mark) by ending the game immediately and awarding a loss to that player. The organisms have evolved past this stage and are making valid moves, although they do not always make intelligent moves. Most of the times that the organism played against a human, it failed to block a winning move or make one itself. Still, even at this stage, it has demonstrated progress, even forcing a human player into a draw in a few test runs.
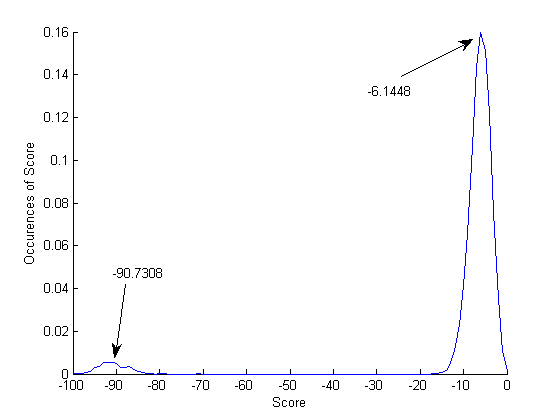
Looking at the MATLAB histogram plot of scores shown below confirms our suspicions. This is a plot of the score achieved by the best organism as evolution progresses. There are two distinct bands, a small one centered at -90.7308 and a larger peak at -6.1448. This suggests that most of the time, there is a mutation that makes one or two organisms perform much better than their unluckier counterparts. It shows that the organisms are getting better in some measure than the previous generation.
Speed of Execution
Each generation lasted approximately 50 seconds, most of which was taken up by the 9,900 games played each round (each of the 100 organisms plays against the other 99). This allows for around 1,700 generations per day.
Safety Considerations
There were no safety considerations neccesary.
Interference
There was no noticable interference affecting other peoples designs from our device.
Usability
When the user is playing against the evolved organisms, the design requires that only one switch at a time is flipped. This is somewhat of an inconvenience when only the switches since the setup is more appropriate for a keypad with a series of buttons arranged like a tic-tac-toe board.
Conclusions
Since we were modeling evolutionary algorithms, we expected it to be slow to converge but it turned out to be much slower than anticipated. This is most likely caused by two factors: we did not use cross-breeding to add genetic diversity to the organisms and we did not prune the game tree by taking into account symmetries or impossible boards. We chose not to use cross-breeding due to the fact that all of the organisms are close enough to each other that cross-breeding would be comparable to mutation. We also chose not to prune the tree because that would involve a good deal more computation to decode the tree into a chromosome that can be stored, adding a new level of complexity to the project.
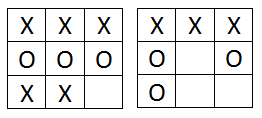
Impossible boards
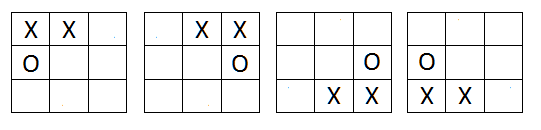
Symmetric boards
Future Work
Possibilities for future work include pruning the game tree, adding the possibility to communicate between Altera development boards to add more organisms to the gene pool in order to speed evolution on, identifying a better metric (i.e. number of draws vs number of losses) with which to evaluate organism performance, or saving the genome to a file on the computer to have data backup as well as the ability to stop and start the simulation without worry.
Appendices
Program Listings
prep2.m (Matlab Evolutionary Algorithm Script)
Evolve.v (Altera Verilog Code)
Evolution.c (NIOS II C Code)
Work Breakdown
| TASK | COMPLETED BY... |
|---|---|
| Conceptualization | Both |
| Evolutionary Theory | Nathan |
| Hardware Setup | Sajeev |
| Algorithm Coding | Both |
| Interface Coding | Both |
| UART Coding | Both |
| Website Setup | Nathan |
| Website Content | Both |
