For this exercise, you will simulate the 2D wave equation on a square mesh in realtime to produce drum-like sounds.
Procedure:
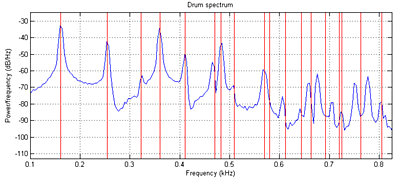
Read Study Notes on Numerical Solutions of the Wave Equation with the Finite Difference Method. The main result you will need to simulate is equation 2.18. A matlab program gives a sequential version of the algorithm and plots the Fourier modes of the drum. Another version is tuned to middle C (261 Hz). You can see in the figure below that the simulated sound spectrum (blue) matches the theoretical drum modes (red) up to about mode 8 or 9 (see Physical modeling with a 2D waveguide mesh for details) .

Modifying the boundary conditions, damping, wave speed, drum size, and distrubution of input energy can modifiy the sound of the simulation from drum-like, to chime-like, to gong-like or bell-like. You can modify the program further to include frequency-dependent damping and other effects. This version simluates a long, thin bar struck at one end.
You will probably want to read
for ideas on parallelization.
Student examples running on FPGA:
(number of wave equation nodes)*(audio sample frequency) 10*(number of wave equation nodes)*(audio sample frequency) . For a minimal 10x10 grid at 44 kHz, you will need 1000x44000=44x106 operations/second. For a more accurate 20x20 grid you will need ~200x106
operations/sec. Clearly some parallel processing will be necessary. Be prepared to demo your design to your TA in lab.
Your written lab report should include: