The bible for my project has been Neural and Brain Modeling (1987) by Ronald MacGregor. His book contains mathematical formulas and FORTRAN code describing various neuronal behavior. My neuron program is based upon his Point Neuron 10, which is a simplified integrate-and-fire neuron model using only four state variables (potassium conductance, membrane voltage, threshold, and a binary action potential spike). This is a simplified version of Hodgkin and Huxley's equations, and is a good enough estimate of neural behavior, especially because the error is negligible compared to the roundoff error from using only 16-bit fixed point values. It should be noticed that real neurons do not exhbit even having 16-bit accuracy themselves.
The small, compact equations are desirable because they are easy to implement in assembly and fit within the 1200's constraints (especially having no RAM and only 32 register spaces, which are not all available because of the need for double-precision fixed point).
The model measures an incoming current, which can be weighted to be either inhibitory or excitatory, and applies that to recalculate "real-time" new values for Gk, Vm, and Threshold by numerical integration. The threshold is then compared to the membrane potential (Vm) and a spike (either a high or low voltage on the output port pins) is generated if the potential exceeds the threshold voltage. These equations which are for a single neuron with a passive RC membrane time constant, a sodium all-or-nothing channel response, and an active potassium channel.
![]()
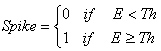
![]()
These equations were then put into a numerical integration scheme using a loop going from t=0 until some end time with some step. The actual assembly program I wrote has no end time and the step time is 1ms.
MacGregor turned the above equations into a FORTRAN program. My project sponsor, Bruce Land, translated that program into matlab code, which I have been using to test the different parameters (Tmem, ampGK, TGK, initThreshold, etc.) to test and debug the neuron code and get it to have certain output properties. The code is given in point.m.
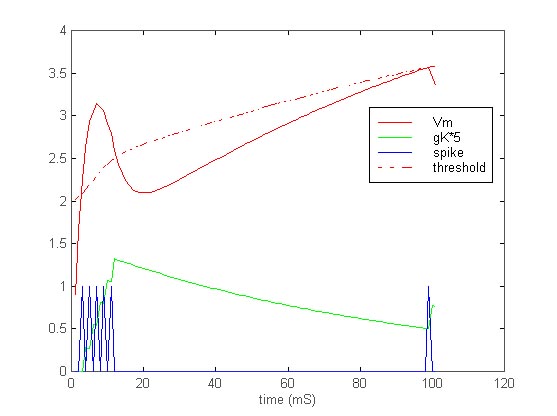
Output of the point.m program, showing change in Vm, GK, Threshold, and the Action Potential output.
Once the single neuron code was "perfected," the next question asked was "what happens if the spike output was fed back into the cell as a depolarizing (positive feedback) current?" We went back to matlab and wrote posi.m, which models this neural model with the current at the next time step equal to the spike output times a weight. This models a single-cell bursting neuron.
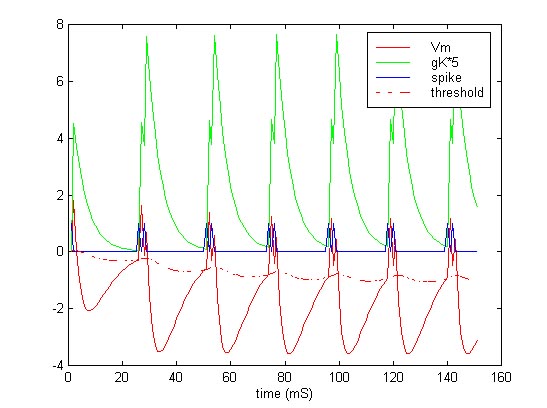
Output of posi.m showing a bursting output pattern.
The next logical step after creating a positive feedback bursting neuron was to combine several neurons together in a cyclically inhibitory network. So a third matlab program was created that (three.m) simulates three neurons connected in a ring with the output of one acting as a hyperpolarizing current on the next one. The result of this was a burst pattern that travels down the line. This data matches the actual circuit results that I built on a prototype board. Five neurons exhibit similar behavior, except that there are two spikes on the line at the same time. This cyclical bursting patter is commonly seen in motor functions
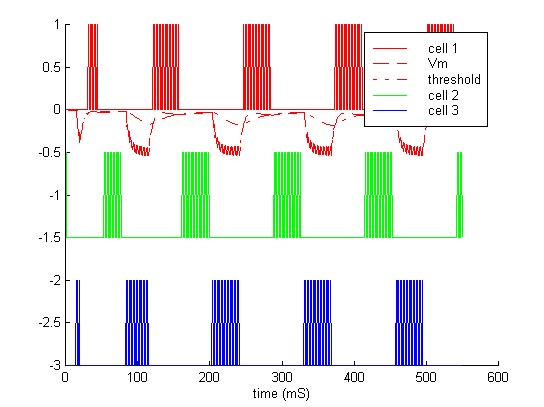
Output of three.m, showing a three-cell cyclically inhibitory network.