OPTIMIZATION OF AN
INTEGRATE-AND-FIRE NETWORK
TO SIMULATE
THE
BEHAVIOR OF A CRICKET
Bart Sautois
CU-ID. 468094
1. Introduction
2. Methods
3. Results
4. Conclusions
5. Source Codes
6. References
1. INTRODUCTION
More and more is understood about the nervous system of humans and animals. And once one understands the basics of it, one of the next steps
is to build models and simulations for it, to be able to do more controlled and thorough testing.
However, the nervous system is very complex, and to build
a realistic model of a nervous system of almost any animal, let alone humans, is a very difficult problem. The system is very high-dimensional, so that even when
the composition of the system would be understood, the configuration of the parameters and different influential factors is still a non-trivial matter.
As a first step in learning about the behavior of neural networks and optimization over a large parameter space in such a network, we decided to start from the simulation of a known system. By using a system that already has been studied and used, we have the possibility of comparing our self-developed results to the previously published data. Thus we are able to make estimates of the accuracy and correctness of our way of simulating and optimizing.
In this project, we started from a simple four-neuron network to simulate the response of a cricket to input-sounds. The model was taken from the paper "A simple latency-dependent spiking-neuron model of cricket phonotaxis" by B. Webb ([2]). We took that network-configuration, and wrote our own programs to implement it in Matlab, using integrate-and-fire neurons.
First we compared different implementation methods on those neurons, comparing efficiency, correctness, etc. Then we used the chosen neuron-implementations to compose the complete network, and started working on a higher level.
Next we needed a measure, a standard, to compare results from different crickets. Once we decided on that, after testing several evaluation-methods, we were able to begin with the actual optimization of our cricket-model.
This led to another difficult decision, as to which optimization algorithm to use. There exists a large number of different optimization procedures, all of which have there own advantages and disadvantages. In the end, we chose to use a genetic algorithm for optimization, because of the ease of implementation, and because tests had shown that the performance was good enough for our purposes in this project.
Finally, using the genetic algorithm, and varying the level of complexity of the parameter set, we were able to find some range of optimal crickets, and to derive conclusions about the possibilities and limitations of this simplified model.
We also wanted to see if it was possible, using this simplified system, to create different "species" of crickets. We defined these different species by a feature that is known to differ among different species of crickets in nature: we changed the time-interval between consecutive bursts of input-sounds. Thus each species of cricket is supposed to recognize its own typical sound.
Finally, we started working with a biologically more correct network, using 6 neurons, and tried to get the same kind of results, by doing optimization through the same algorithms and programs.
2. METHODS
Neural model
As neural model we have chosen to use the integrate-and-fire model. It is both a good approximation of neural actions, and it is quite easy to program and to understand. It has a great speed advantage because the computations can be done relatively fast.
It is a single-compartmental model for a neuron, which uses one potential-variable to indicate the condition the neuron is currently in. So the model is simplifying in this way that it supposes that the membrane potential is the same for the whole neuron. In practice this isn't always the case.
An action potential is generated when the membrane potential of the
neuron reaches a certain threshold. After the action potential, the membrane potential is
brought back to a fixed level below the threshold. This level is called the
resting potential of the neuron. It is also the level of the membrane potential when the neuron doesn't get
any inputs.
Immediately after each action potential, the possibility to generate another
spike is delayed, by incorporating a refractory period: during an absolute
period of time, the potential of the neuron is kept constant at
resting level. It is only after this period that it can rise again, and that
possibly a new action potential is generated.
Each neuron also has an adaptation-level. This is a variable that simulates the decaying influence of the consecutive external inputs on the neuron. In reality, when a neuron gets a series of incoming action potentials, the influence from each individual action potential on the neuron becomes smaller. This is modeled by the adaptation: with every incoming action potential, the adaptation is augmented with a fixed value (Ginc), after which it decays very slowly, until another spike is generated. And this adaptation term is used in the computation of the change in membrane potential of the neuron as a result of incoming spikes.
We added a lot of functionalities, of which we removed some again later, although leaving the possibility of re-entering them in the future. An example of such a functionality is the change of synaptic weights due to action potentials passing through. In reality synaptic strengths can decrease or increase as action potentials go trough them.
Integration method
As for the integration method used for the implementation of the model described above, we
started off with Euler interpolation and second order Runge-Kutta interpolation.
Both methods are used to solve problems of the form
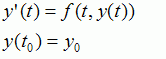
The Euler method is based on the formula
![]()
with ![]() being the step size.
being the step size.
The second order Runge-Kutta method uses the following formulas:

Later on, we switched to the Euler method with linear
interpolation, as described in "On numerical simulations of integrate-and-fire
neural networks" by D. Hansel, G. Mato, C. Meunier and L. Neltner ([3]).
This method is based on the Euler method, but it is a lot more accurate. The method is
different from the regular Euler method at the times of spiking: then it computes
the actual time of the spike more accurately by using linear interpolation on the two most recent
data points (the begin- and end-value of the last step).
As a consequence, the end of the refractory period will also be computed more
accurately, and thus also the point of time at which the membrane potential starts to rise again. This way, all future
spike times will be influenced by each linear interpolation that is computed.
This method has the ease of implementation and speed of computation of the Euler method, yet is almost as accurate as the second order RK-method.
Network configuration
Faze 1
The basic outline of the network we used for our experiments
was based on the article "A simple latency-dependent spiking-neuron model of
cricket phonotaxis" by B. Webb and T. Scutt ([2]).
It is a simplified network consisting of 4 neurons (see Fig.1).
2 ascending neurons, AN1 neurons, left and right (ANL and ANR), receive auditory input from left and right ear
respectively.
Each of these AN1's has an excitatory connection to an ipsilateral motor neuron
(MN), and an inhibitory connection to a contralateral MN. These MN's send output to the muscles that control the body motion.
Because of the configuration, if both AN1's are equal in their parameters, a MN will
typically have an increase in its potential when the ipsilateral AN1 neuron starts firing
before the contralateral AN1 does.
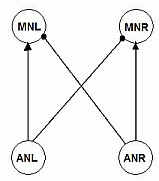 |
Fig.1 Experimental neural network: 2 Ascending Neurons of type AN1, left and right (ANL and ANR) have connections with excitatory synapses to the ipsilateral Motor Neurons (MN's) and with inhibitory synapses to the contralateral Motor Neurons. |
The parameters of this network were determined experimentally, to generate an
optimal network.
Faze 2
In the second faze, we wanted our model to be more biologically correct. In reality, the inhibition of movement of one side of the body does not happen
through inhibition of the AN1's to the contralateral MN's. Instead, there is a third type of neuron involved, the Omega Neurons (ON1). They are called this way, because of their shapes, that resemble
the Greek capital Omega-letter. There is one ON1 on each side of the body (in the head).
These ON1's receive the same auditory excitatory input as the AN1's, directly from the ipsilateral ear. When spiking, an ON1 inhibits both the contralateral AN1 and the contralateral ON1.
 |
Fig.2 Biologically more correct neural network: 2 Ascending Neurons of type AN1, left and right (AN1L and AN1R), have connections with excitatory synapses to the ipsilateral Motor Neurons (MN's). 2 Omega Neurons of type ON1, left and right (ON1L and ON1R), get the same input as the AN1's, and have connections with inhibitory synapses to the contralateral AN1 and the contralateral ON1. |
Experimental setup
All experiments were done mathematically, by simulations,
using Matlab. To get some kind of visual form of comparison, we built a simple
and small system: we placed a sound-source at a certain position in a 2D plane, put
a simulated cricket in a different position, and made the cricket move according
to the output of the simulated nervous system, the output of the MN's.
In Fig.3 you can see the test-plane: the sound source is indicated
by a small cross, the cricket is represented by 3 circles: it's body, enclosed
between its 2 ears. These ears are so big, to show the time-delay between the
sounds, received in both ears. This sound delay is significant enough to be
detected by our network, simply by comparing and working with the spike trains, although by eye one hardly sees the difference.
The default behavior of the cricket is to move straight forward; our neural network tells it when to turn. And because the sound source isn't right in front of the cricket, the sound-delay in both
ears will cause the system to indicate necessary turns.
 |
Fig.3 View of the test-plane. The small 'x' indicates the position of the sound source, the cricket is represented by 3 connected small circles: its body and ears. |
Optimization methods
Faze 1
First we wanted to test the influence of the synaptic weights on the cricket's behavior (the system's output). This had the big advantage that the searches only happened over two free parameters, i.e. in 2D-space, and thus the results could be plotted out as a surface. This enabled us to get some visual idea of the results.
After building a relatively successful cricket, we still needed to optimize the rest of its parameters, to find an optimal cricket, and maybe find the key between different "species" of
crickets.
We already had some general idea of realistic and good value-ranges for some of the parameters, but we wanted to be able to localize an optimum in a greater
parameter space. Therefore we tried to find that optimum by using the "fminsearch"-function
in Matlab. But because of the nature of the surface (a lot of flat plateaus), this function did not give
the results we hoped for. The optimal values that were returned, were mostly very local, and thus extremely dependent on the initial point.
So we turned to another method: we started optimizing by implementing a genetic algorithm, based on the chapter "Optimization of swimming locomotion by genetic algorithm" by D.Barrett in the book
"Neurotechnology for biometric robots" ([5]).
The algorithm works as follows:
You start by building the "definition" of an instance of the object that has to
be optimized, i.e. listing all parameters that are to be optimized by the
genetic algorithm. Then you have to choose the ranges of values for each of the
parameters. These decisions are up to the programmer, and can influence the outcome and performance of the algorithm
significantly.
The algorithm then starts with one generation, consisting of a certain number of species
(i.e.
parameter sets). The values of each of these parameters in each of the animals is chosen at random from
the ranges for the respective parameters. Then the program evaluates each of these animals and keeps only half of
them: those that gave best results.
After this the actual genetic part of the algorithm takes place:
- Reproduction: the remaining animals are doubled, such that we have again the full number of parameter sets.
- Crossover: divide the parameter sets in pairs, and for each pair of animals, a certain place in the list of parameters is chosen at random, and all
parameter values after that place are
switched between both crickets. This is the kind of crossover as it happens with chromosomes at the duplication of a cell.
- Mutation: by a fixed (low) probability, one parameter in the whole generation gets a random new value. This probability must be determined by the programmer, but is typically dependent of the number of animals per generation and the number of parameters per animal.
To avoid the creation of a kind of cricket that is tuned to only one specific sound location, we tested each generation on several sound locations, by each time picking a new random angle between the cricket's initial position and the sound source, from the interval [0, pi/3]. The whole generation was then tested against the same small series of angles, and the average of the scores was taken as the final score for each cricket. s\This way, a resulting cricket should perform well on a good number of positions within that range.
We also considered the use of a variant of simulated annealing, but we decided not to, for several reasons. The most important reason was the ease of programming and the understandability of the program. This system was intended to get an idea of the general principles of such a system, of what the possibilities are, how far we could drive it, etc. The genetic algorithm seemed to work well, and was relatively easy to program and to understand. Simulated annealing would increase the complexity of the program, while probably not increasing the performance terribly much.
From all crickets that came out of different runs of the genetic algorithm, we extracted the best one, by testing each
"converged cricket" on the same big number of different sound source positions.
The best cricket was the one reaching the most sound sources and defined to be "species A".
After that, we did the whole optimization process over again, to create "new species".
We defined these new species by changing the interval between different bursts of
input sounds in the optimization process. This is a feature, known to differ between different species of crickets in nature.
After creating different species like that, we wanted to compare them in parameters and in performance, to see if there
were certain parameters that were significantly different. These would then determine to
which inter-burst-interval a certain species of cricket would respond.
Faze 2
With the biologically more correct system, we basically ran the same tests, used the same algorithms. Again we wanted to find the optimal parameter setting for the cricket-simulation. Because of the generic nature of the code, it was fairly easy to adapt the code to the slightly more complex system.
From the plots and data from [7], it was clear that the ON1's had practically the same parameter values as the AN1's: time constants, threshold, resting potential... All seemed to be very similar or equal. So that gave us a lot of tight constraints on the new neurons, even before any of the optimizations.
3. RESULTS
Different comparison measures
To test and compare the different parameter settings of the cricket, we tried different evaluation schemes. In all tests we let the cricket move for a limited period of time,
approximately equal to twice the time it would need if it would move in a straight line towards the sound source.
At the same time we tested the influence of the synaptic weights on the
cricket's performance. Because this is a 2D-search, we could plot out the
results of all crickets as one big surface, and have a visual image of the
results. This also simplifies the comparison of the different comparison
measures.
First we computed the minimal distance that is created between the sound source
and the middle of the cricket's body, at any point of the cricket's path through
the plane. (Fig.4a)
Secondly, we recorded the time needed by the cricket to get within a certain
very small range of the sound source. If the cricket never got there, the
end-time of the interval was returned. (Fig.4b)
Finally we measured the "angular delay" of the cricket's path to the sound
source. To do this, at each point in time, we computed the difference in angle
between the cricket's current orientation and the angle of the straight line
from its position to the sound source. The absolute value of this
angle-difference was added to our comparative measure. The total sum of the
angles, until the cricket gets within a certain small range of the sound source,
forms the resulting value. (Fig.4c)
We applied each of the performance-measures to a large number of different crickets, using as parameters a wide range of values for the 2 synaptic weights. We chose the synaptic weights to be symmetric and non-variable. So both excitatory had the same weight, as did both inhibitory synapses, at all times during a run of the program. (See Fig.4)
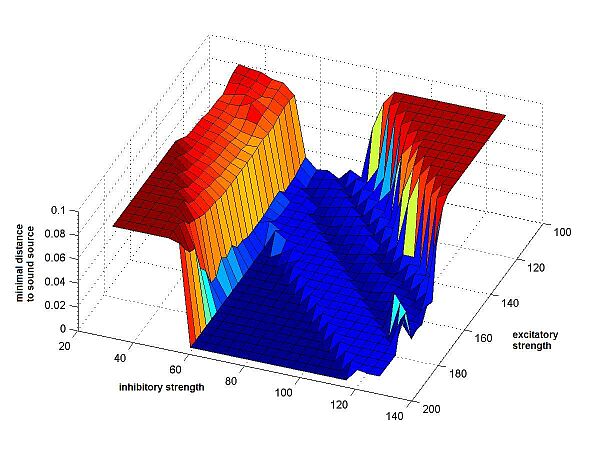 Fig.4a Minimal distance from sound source |
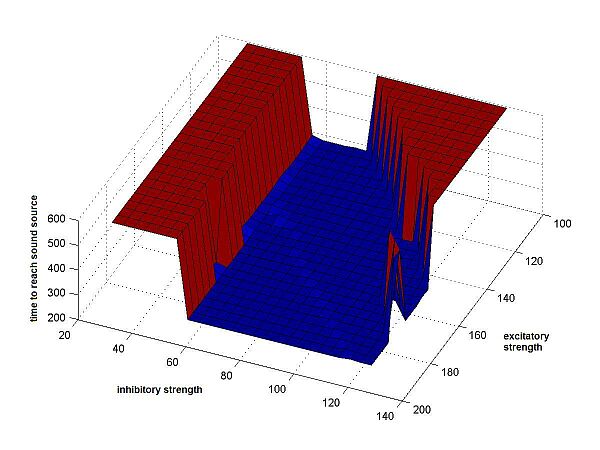 Fig.4b Time to sound source |
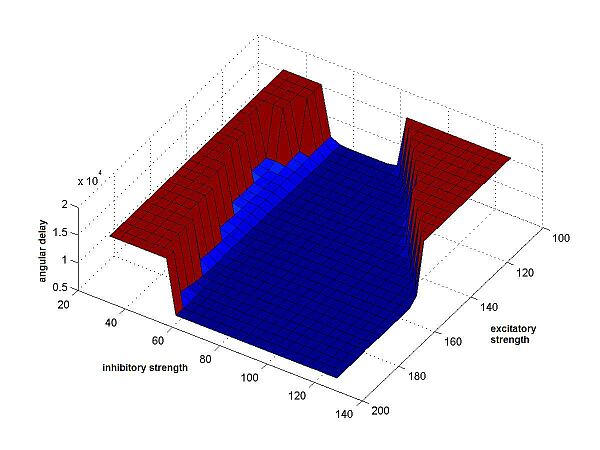 Fig.4c Angular delay along path |
|
Fig.4 Resulting surfaces for the 3 different
performance measures. On the axes, the synaptic weights have been multiplied
by 10. The values of the excitatory synapses range from 10 to 20, the values
of the inhibitory synapses from 3 to 13. Along the z-axis the results are shown, as returned by the cricket-function, results that have different meanings
on each plot: 3a The result is the minimal distance between cricket and sound source, at any point along the path of the cricket. 3b The result is the time it took the cricket to get within a small area around the sound source. If this area is never reached, the end of the time interval (600) is returned. 3c The result is the angular delay: the sum of absolute values of the differences in angle between the cricket's orientation and a straight line to the sound source, at each point along the path, until the sound source is reached or time has run out. |
As can be seen, all of these three measuring schemes
gave very comparable results. The surface of the weight-interval was always
similar: a large valley, shaped like a wedge, and apparently infinite, with
steep slopes that lead to plateaus of very bad values.
The distance-measure gives a more uneven result than the other 2 measures.
The uneven valley floor is caused by the fact that the cricket doesn't always
reach the sound source with the middle of its body, but sometimes with its ears,
which causes very small differences in the minimal distance. In reality however,
these small differences wouldn't matter: if the cricket reaches the sound
source, the other cricket, that is sufficient.
On the higher plateaus there is also less flatness. For the time-measure, when a
cricket doesn't reach the source, simply the end of the time-interval is
returned, which is the same in all cases. The minimal distance of the cricket to
the source, however, can be very different. This is what causes the variation in
bad values. But also these differences aren't always equally important: unless
the cricket comes very close, one is mostly only interested in whether the
cricket gets there or not; if not, than the model simply doesn't suffice.
What was also very unexpected was the shape
of the resulting surface for the angular delays. It is very similar to the
time-measure, and the most flat of all three surfaces.
Important is that the valley floor
of the time-results isn't as flat as it appears to be on the plot shown above (Fig.4b).
This is clear when looking at Fig.5,
which shows a close-up plot of the time-measure-surface.
 |
|
Fig.5 Detail of the valley floor of Fig.4b, the time-measure-surface. This detail shows that the valley floor is less flat than it appears on the large plot. It shows that the surface is relatively uneven, and that there will not be one single minimum. |
Fig.5 shows that there is more unevenness in the valley floor than is visible at first. It turns out that these differences are minimal, but noticeable in the cricket's motion: when running the program for different synaptic weights, one can see slight differences in the crickets movements, different, slightly longer turns seem to be taken. However, this difference is minimal, as can be seen in the movie-files downloadable below.
movie 1: Cricket motion for a cricket with excitatory strength = 16 and inhibitory strength = 7
movie 2: Cricket motion for a cricket with excitatory strength = 16.5 and inhibitory strength = 8.75
After these tests we decided to continue with the time as primary
comparison criterion. We chose it because it is more intuitive than the angular
delay, and the differences in the distance-measure aren't all equally important,
as explained above.
Optimizing the parameter settings
Faze 1
To this point we had been able to note some of the possibilities of changing the synaptic weights, and we wanted to move to a higher dimensional parameter space. By testing some other pairs of parameters in 2D-space, we had discovered that probably all parameters are closely linked, and no small number of parameters determines the whole behavior of the cricket.
In the genetic algorithm described above, we had to make a
few decisions on initializations.
We chose each cricket to have 5 variable parameters, to be optimized by the program:
the 2 synaptic weights, tMemb (time constant of the membrane), tAdapt (time constant for the adaptation of the membrane) and Ginc
(the amount of adaptation after a spike).
These 3 last parameters were to be the same for all 4 neurons in the system.
As for the ranges of these parameters, we chose not to put any tight restrictions on any of them, although we had very strong suspicions that
for example the synaptic weights would be between 15 and 30, etc. We preferred to let everything be discovered, be optimized by the algorithm itself.
Thus, we chose the synaptic weights to have ranges from 0 to 45, tMemb from 0 to 10, tAdapt
from 0 to 100, and Ginc from 0 to 0.06.
The mutation-probability was chosen in such a way that, on average, every two generations one of all parameters over the whole population would be mutated.
Finally, the last thing we had to choose, was the number of animals per generation, which we set at 12.
It turned out that every time the algorithm converged to one specific parameter setting. The amount of generations this took, however, was highly variable.
On every parameter setting that we got as result from the genetic algorithm, we ran extra tests: we tested them by running them on 50 random sound source positions.
In general, the results were good, but none of the parameter settings resulted in the cricket reaching the sound source at every position tested.
So probably the system is too much simplified to create a cricket that works well on all possible sound source positions. However, what these tests were really good for, was to get an idea of plausible parameter
ranges for all parameters, instead of the very general ranges we started with in
our optimization algorithm tests.
We ran all of the crickets, generated by the genetic algorithm, against the same large
set of random angles, to compare them. We calculated what percentage of the tests were
successful (in what percentage
of the tests the cricket actually reached the sound source), by using the time-measure. We also used the distance-measure, calculating the average minimal distance over all
successful tests, and
the average minimal distance over all unsuccessful tests, for all crickets.
From the data collected from these tests, we decided which cricket gave
best results overall, and designated that cricket as "species A". All the tests done so far, were done with
input sounds consisting of bursts, interleaved with intervals of length 40 ms.
(see Table 1)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 1 The top table shows the parameters of 5 crickets that resulted as output of the genetic algorithm. Some parameters, Ginc and tAdapt, have relatively big deviations. Indicated are cricket number, weight of the excitatory synapses (Exc.Str.), weight of the inhibitory synapses (Inh.Str.), time constant of the adaptation (tAdapt), time constant of the membrane (tMemb) and the step size of increase of the adaptation (Ginc). The bottom table shows the results of each of these crickets, when tested against a list of 50 random sound source positions. All crickets were tested using the same positions. Indicated are cricket number (referring to the cricket number from the top table), percentage of the tests in which the cricket reached the sound source (successful), average minimal distance to the sound source in the unsuccessful tests (avg.bad min.dist.) and average minimal distance to the sound source in the successful tests (avg.good min.dist.). The table shows that cricket 5 gives the best overall rate of success, so "species A" was defined by the parameter set of cricket 5. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Then we did the same optimization procedure again from the start, with inter-burst-intervals 50 and 80. This way, we wanted to check the
possibility of creating new "species" of crickets,
using the same system, and only changing the 5 parameters we had varied so far.
We wanted to know to what extent the behavior would change, and how different
the parameters would be.
The procedure was exactly the same, and thus we ended up with 3 optimal crickets, 3 different species:
a 40-cricket, a 50-cricket and a 80-cricket. To compare them, we ran each of
these crickets on a wide range of random angles (again), for various
inter-burst-intervals.
This was done to test 2 basic properties:
- whether each cricket would effectively be the best of the 3 on its own "trained"
inter-burst-interval
- whether each cricket would better on its "trained" interval than on
all other intervals.
The results are shown in Table 2.
|
exc = 37.299750; inh = 29.873772; adapttime = 42.590859; membtime = 6.273886; gincrease = 0.004187; (optimized for inter-burst-interval of 40)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
exc = 33.518290; inh = 33.288996; adapttime = 17.138248; membtime = 7.530666; gincrease = 0.007406; (optimized for inter-burst-interval of 50)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
exc = 19.552808; inh = 22.128343; adapttime = 66.691257; membtime = 3.663993; gincrease = 0.034978; (optimized for inter-burst-interval of 80)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 2 The top table shows the 5 parameter values and the behavior of the cricket that was optimized for inter-burst-interval 40. The bottom table does the same for the 80-cricket. The middle table shows that same data for the 50-cricket, over a smaller range of inter-burst-intervals. Above each table are all parameter values listed for the specific species. The table indicates inter-burst-intervals (interval), percentage of the tests in which the cricket reached the sound source (successful), average minimal distance to the sound source in the unsuccessful tests (avg.bad min.dist.) and average minimal distance to the sound source in the successful tests (avg.good min.dist.). The 50-cricket was tested over the less inter-burst-intervals, but it is clear from the given data that its behavior is very close to that of the 40-cricket. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
The only parameter that seemed significantly different between the crickets coming forth from the genetic algorithm for the different inter-burst-intervals, seemed to be tAdapt, which was a lot bigger for the crickets with interval 80. But it was also obvious from previous tests that the deviations in tAdapt are very large for the different crickets of each species individually as well.
The other results were even more unexpected: both the crickets for optimized inter-burst-intervals 40 and 50, perform close to optimally for interval 30, and then perform worse when the interval length increases. So these crickets' best interval is not the interval they were optimized for.
And the 50-cricket is not the optimal species of the three for the inter-burst-interval 50.
For intervals 10 and 20, all crickets seem to perform badly.
The cricket optimized for inter-burst-interval 80 is different: its best interval is the 80-interval, but now its performance is very bad overall. In fact, its performance at interval 80 is only very slightly better than the behavior of the cricket optimized for interval 40, a small difference that could just as well have been caused by luck as by the algorithm.
So now the question
was whether this obvious lack of combining power for
selectiveness and good performance was inherent in
the system, or whether it could be solved my making the system slightly more complicated, without changing anything to the initial construction.
So we changed the number of parameters per animal from 5 to 8, by making tMemb, tAdapt and Ginc
different for AN1 and MN neurons. So both AN1 neurons would still have the same
values for these parameters, but these could be different from the values for the MN neurons. We ran the whole
optimization scheme again for the worst species so far: the one with
inter-burst-interval 80; the results for the cricket are listed in Table 3.
Now the overall performance is better, but the interval of length 80 is not the
optimal interval anymore. So we gained on one property, but lost the other.
|
exc = 31.482102; inh = 42.180104; tAdapt AN neurons = 8.070847 tAdapt Motor neurons = 19.941288 tMemb AN neurons = 9.699823 tMemb Motor neurons = 2.377668 Ginc AN neurons = 0.009127 Ginc Motor neurons = 0.035844 (optimized for inter-burst-interval of 80)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Table 3 Above the table are all parameter-values listed for the cricket. The table indicates inter-burst-intervals (interval), percentage of the tests in which the cricket reached the sound source (successful), average minimal distance to the sound source in the unsuccessful tests (avg.bad min.dist.) and average minimal distance to the sound source in the successful tests (avg.good min.dist.). |
||||||||||||||||||||||||||||||||||||||||||||||||||||
Faze 2
Initially, we wanted to try to get a good working system with as few changes as possible.
First we took the parameter setting from the optimal cricket we had gotten so far for an inter-burst-interval of 40 ms (see Table 2). We gave the ON1 neurons the same parameter values as the other types of neurons, and they were all fixed. Then we searched in 3-parameterspace by making the synaptic strengths of the connections the only variables: the excitatory AN1-MN weight, the inhibitory ON1-ON1 weight and the inhibitory ON1-AN1 weight. But no good results came of it.
The following is meant by "no good results":
We let the genetic algorithm run, and let it print out it's results after each
generation. In each generation all crickets were tested against 5 different
sound source angles.
Most times, we got just all values 600 for all crickets (= the crickets never
reaches the sound source). Sometimes, we got something around 570 or so for all crickets: this means that 1
of the 5 angles tested at that generation was so small, that all crickets,
although only moving straight or turning very slightly, still would reach
it fast. Averaging one fast time with 4 600-times would give a value between 500 and 600.
If after 3 generations, there was no distinction between the different crickets,
and all values were bad in all 3 generations, we interrupted the run, and
restarted with a new one. This would result in better chances of getting a good-performing cricket.
Secondly, we moved to a 6-parameter space, by making tMemb, tAdapt and Ginc
variable too. we used the same values of these parameters for all 3 kinds of
neurons.
Again, no good results came out of the genetic algorithm.
As a third test, we moved to a 9-parameter search, by splitting tMemb, tAdapt and Ginc
up: AN1 and ON1 still got the same values (since that idea is supported by data
from [7]), but MN's values could be different.
Again, no good results.
For each space (3, 6 and 9) we did about 5 to 10 of these tests, none of them were any
good.
Once in 9-parameter space, it seemed to work better, so we let it run to 8
generations. After that, there were 2 crickets left, that seemed equally good.
But when we let them both run against 50 different angles, it turned out they
both only reached the source in about 8% of the cases. So it wasn't any good
after all, especially when comparing this result to the results we got in the
more simplified system.
We figured that something else must be changed to get the algorithm to converge to a decent-working
parameter setting.
One thing that seemed logical was to use delays: up until now, the excitatory input from the ears to the AN1 and ON1 arrived at the same time. But this also means
that the inhibitory effect of the sound to AN1 is delayed (because it has to be processed first by ON1.
So what we tried is to delay the excitatory
input from the ears to the AN1 by a certain number of time steps. That way,
inhibitory and excitatory inputs would arrive at AN1 in a variety of
time-differences. We tried delays of 1,2,3 and 5 time steps.
None of these modifications improved the results we got in a considerable amount. There was one
parameter setting, at a delay of 2 time steps, that seemed to work better than
previous tests. But after running that setting against 50 different angles, it
still only got to about 16% of the sound sources, which is still a poor result, when compared to the percentages we got in our more simplified system.
4. CONCLUSIONS
By comparing the data of Table 3 to the results given
in Table 2, one can draw several conclusions.
The overall performance of a cricket can be increased considerably by making
more parameters variable in the optimization process, thus making the system
more complicated, more costly to compute, however without changing the
construction of the neural network. But an increase in the overall performance
seems to cause a loss of selectiveness of the cricket. It seems as though
performing well overall is tightly coupled with have an inter-burst-interval of
30 or 40 as optimal interval.
This doesn't seem completely illogical: a shorter inter-burst-interval means
that over one time-interval, more information comes in, and thus better
discrimination is possible.
So using the simplified model described above, it is already
possible to simulate a cricket that responds relatively well to sound sources from different angles. However, when the angle is too big (bigger than
pi/3), the crickets will almost never reach the sound source. And there seems to be no cricket that responds optimally to all possible sound source positions in the range of [0,pi/3].
It turns out that the inter-burst-interval is significant for the cricket's response. There seem to be two possible choices in the optimization objective.
If your objective is to create a cricket-model that performs as good as possible overall, that is possible. But its optimal inter-burst-interval will always be around 30 or 40, and the performance
will decrease as the interval increases.
You can also choose to optimize a cricket for a specific inter-burst-interval, and then it is possible to create it such that that specific inter-burst-interval will be its optimal interval. However,
the overall performance will be relatively bad, and even in the trained interval the performance will be only slightly better than the performance of the general-performing model.
And indeed, these result are supported by biological data: as is already mentioned in [7], probably AN1 and ON1 are used primarily for
song recognition, which would be equivalent to the selectivity
of our system to specific inter-burst-intervals. And that does work pretty good, as is obvious from Table 2.
That same paper suggests that the actual localization is initialized by other neurons, namely AN2. But since relatively little is known about the behavior of that type of neurons, it isn't
modeled very
often. Its responses to different inputs can be very diverse and variable.
This shows that it is only natural that the simplified system we modeled, is only capable of doing one of both functions: either recognition (= selectivity) or localization.
A limitation on the recognition is that this very simple model does not seem to be capable of responding solely to a limited range of inter-burst-intervals. The performance will be less good at other intervals, but there will always be a response to some percentage of 'bad' sounds, no matter how different the other inter-burst-interval is. So there is need for a more complicated model to be able to create actually separated "species" of crickets.
Contradictorily, the biologically more correct system seems
to work less good so far. Localization has failed almost completely in all tests
we have done up until now.
And because there is hardly any good response to any location of the sound source, it is impossible to do selectivity tests on this simplified model.
There is probably some (biological) data missing to build a more successful system, or some parameters are set wrong. Maybe we need to add some delays, or variable synaptic weights...
5. SOURCE CODES
- eicricket.m: Example cricket where the numerical integration was implemented using Euler's method with linear interpolation; it returns the minimal distance as result.
- anglecricket.m: Analogous cricket as 'eicricket.m', but returning the angular delay as result, instead of the minimal distance.
- movingcricket.m: Analogous cricket, generating more output: it shows the movement of the cricket throughout the computations, and shows output for the 4 different neurons in the system (potential, adaptation, spike train).
- mostparams.m: Most detailed cricket we optimized with the limited system, using the genetic algorithm.
- genetic.m: Genetic algorithm to optimize the parameters of a cricket (in this file: mostparams.m).
- testbursts.m: Example program to test a certain cricket against a large number of sound source positions over a wide range of inter-burst-intervals.
- newcricket9.m: Most detailed, biologically more correct, cricket from faze 2, with 9 parameters.
6. REFERENCES
[1] P.Dayan, L.F.Abbott, (2001), Theoretical Neuroscience, MIT Press.
[2] B.Webb, T.Scutt, (2000), A simple latency-dependent spiking-neuron model of cricket phonotaxis, Biol.Cybern. 82, 247-269.
[3] D.Hansel, G.Mato, C.Meunier, L.Neltner, (1998), On numerical solutions of integrate-and-fire neural networks, Neur.Comp.10 2: 467-483.
[4] R.J.MacGregor, (1987), Neural and Brain Modeling, Academic Press.
[5] Ayers, Davis, Rudolph (editors), (2002), Neurotechnology for Biomimetic Robots, MIT Press,
D.Barrett, Chapter 10, Optimization of Swimming Locomotion by Genetic Algorithm, pp.207-221
[6] H.Roemer, M.Krusch, (2000), A gain-control mechanism for processing of chorus sounds in the afferent auditory pathway of the bushcricket Tettigonia viridissima (Orthoptera; Tettigoniidae), J.Comp.Physiol. 186,181-191.
[7] D.W.Wohlers, F.Hueber, (1982), Processing of sound signals by six types of neurons in the prothoracic ganglion of the cricket, Gryllus campestris L., J.Comp.Physiol. 146,161-173.
[8] A.I.Selverston, H.-U.Kleindienst, F.Hueber, (1985), Synaptic connectivity between cricket auditory interneurons as studied by selective photoinactivation, J.Neuros. 5, 1283-1292.
[9] Z.Faulkes, G.S.Pollack, (2001), Mechanisms of frequency-specific responses of omega neuron 1 in crickets (Teleogryllus oceanicus): a polysynaptic pathway for song?, J.Exp.Biol. 204,1295-1305.