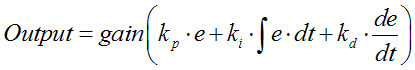
High Level Design
 

Rationale

The idea of a light tracker came from Professor Land as an idea for a possible ECE 476 motor control lab. The ECE 476 course already had a temperature controller lab that involved basic motor control, but the controller in that lab simply turned a DC fan on and off in response to tine input from a temperature sensor. The proposed light tracker lab would require more precise control over the motor and the input from the sensors would be used to directly calculate the motor’s degree of response. The photo-resistors that were used in the light tracker were chosen because they were simple to use and could be used with a simple voltage divider circuit and the ADC’s on the Mega32. Also, the servo motor was chosen because of its generic nature and because it could be controlled through the microcontroller’s PWM.

Background Math

The PID algorithm is based on the following equation:

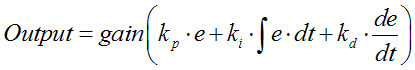
The term ‘e’ is a function represents the error in the system, or in context of the light tracker problem, the difference between the outputs of the light sensors.  The output is a weighted sum of the error, the integral of the derivative function, and the derivative of the error multiplied by a ‘gain’ value.  The output is a signal sent into the system that ideally should minimize the error as time progresses.  Thus the output is used to correct the position of the servo to ideally obtain a zero error.  The three terms in the above equation are known as the Proportional, Integral, and Derivative terms respectively.  Using just the proportional term to drive the output tends to make the system overshoot as its trying to minimize the error.  In terms of the light tracker, it will make the servo oscillate back and forth as it tries to find a position that will make the inputs to both of the photo sensors equal.  Adding the derivative term will make the system settle faster since its value depends on the slope of the error.  Thus if the error is either increasing or decreasing rapidly, the derivative term will be a large component of the output to drive the system in the direction of zero error.  Thus the derivative term will make the system more stable by applying larger correction if there is a rapid change in the error.  The purpose of the integral term is to reduce the sum of squared errors in the system.  If the error becomes small and constant, the proportional term and derivative term will also be small; however, the integral term is essentially a running average, so it eventually accumulates all of the small errors and apply the appropriate correction to the output.  As a result, the integral term will increase the settling time as it slowly moves the system toward zero error.  Intuitively, the proportional and derivative term will make the light tracker quickly move toward the light source, and the integral term will handle the small corrections so that the light tracker will point exactly at the point where the light sensors report that same output.  Lastly, the ‘gain’ value is the overall gain of the PID control, technically, it can be combined with the and term weights.  Initially set all of the weights to a low value and increment them until the desired operation is reached.  If the tracker is constantly overshooting, turn down the 'gain' term and raise the term. 

Logical Structure

The control program for the light tracker polled the Port A input pins for the light sensor output and controlled the servo motor with a PWM output from Port D.  The program is divided into four principle components: the kernel, the sensor handler, the servo controller, and the button handler.  These components are detailed below

• Kernal: The kernel of the control program was relatively simple as it simply refreshed the sensor handler and servo controller every 10 ms.  The kernel also initialized the ADC used by the sensor handler and the PWM on timer 1. 
• Sensor Handler: The sensor handler took the inputs from the ADC on pins 1 and 2 of PORT A.  The raw sensor data is multiplied by an adjustment factor that adjusts for the fact that the sensors were not exactly matched.  The sensor data is then differenced to obtain the error of the light tracker.  This module keeps track of the last value of the error to calculate a simple derivative using a divided difference approach and approximates the integral as a running sum. 
• Servo Controller: The servo controller uses the error, derivative, and integral computed from the sensor hander to compute a correction using the PID equation.  The weights in the PID expression were determined through trial and error. 
• Button Handler: This module handles the input from the buttons, by debouncing them and flagging to other modules when buttons are pressed.  Depending on which button is pressed, the gain or one of the proportional, integral, or derivative term weights is changed. 

Since the light tracker does not broadcast anything and is not intended as a commercial product, it does not meet with or comply to any IEEE, ISO, ANSI, DIN, or any other standard. 

Existing Patents

            There are multiple existing patents that are relevant to the servo based light tracker.  US patent number 6,947,073 defines an apparatus and a method for tracking moving targets.  This patent is quite general and could be extended to a light tracker that follows a moving light, much like the tracker described in this document.  US patent number 6,926,673 discusses a method to track the position of an ultrasonic beam.  Although this patent does not mention any kind of moving apparatus, it does track energy, in this case sound, emitted by an object much like a light tracker.