High-level Design:
Hardware:
Mazerunner runs on an Atmel ATMega32 chip. The chip's output signal runs through a DAC to a video monitor. All user input is taken through two Sega Genesis game controllers.
The Game:
The general format of the game is that a player is locked in a maze that has only one solution and must escape the maze to win. At the beginning of the game, a number of keys are placed randomly throughout the maze. The player must first "pick up" all of these keys by moving over them. Once all of the keys have been picked up, an exit will appear at a random location along the outer wall of the maze.
Oh yeah, did we mention the monsters? A number of monsters may be moving randomly about the maze as well. If the player comes in contact with one of these monsters, the player loses one life and is re-spawned in a randomly-selected corner of the maze. If a player is "eaten" by monsters three times, the game is lost.
Sequence:
At reset, a title screen appears. The user is prompted to "press C" to move to the next screen, where they may choose to play a progression game or single game. A progression game consists of 10 levels with preset numbers of monsters and keys played in series. During a progression game, a player can only be eaten a total of three times; after the third time a player is eaten, they do not advance to the next level.
If the user opts for a single game, they may choose the number of players (1-2), monsters (0-3), and keys (1-4) to have in their maze. In two-player games, it does not matter which player picks up any given key, but if either player is eaten 3 times, the game is lost, and once an exit appears, both players must reach it to win the game.
At the end of the game, a score is determined based on the difficulty of the maze (ie. the number of monsters and keys), the time taken to complete the maze, and, in the case of a progression game, the number of mazes completed.
Maze Algorithm:
This algorithm produces a single-solution maze - that is, a maze in which there is only one path between any two points.
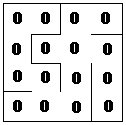
Logically, the maze is represented as a 2-dimensional array of cells. Our maze is size 10x10, but for simplicity, I will show an example here of the creation of a 4x4 maze. The maze is initially set up with each cell in its own set and walls between every cell, as shown here:

The algorithm randomly selects a cell and randomly selects another, adjacent cell. It then checks the sets to which these cells belong. If they belong to different sets, the wall between them is removed, and they (as well as every other cell already connected to them) are placed in the same set. If they are already in the same set, they are already connected, so the wall is left in place. This process is repeated until all cells are in the same set.
Here is an example of how a 4x4 maze might be connected:

Randomly select element 5.
Randomly select adjacent element 6.
Check to see if 5's set is the same as 6's set; (5 != 6), so:
Knock down wall, put cell 5 & 6 in same set.

Randomly select element 6.
Randomly select adjacent element 2.
Check to see if 6's set is the same as 2's set; (5 != 2), so:
Knock down wall, put cell 6 (and 5) & 2 in same set.

Keep repeating the process...
Eventually, all cells will be connected: