RP2040 ROSC

Cornell University ECE4760
Random number generators for
Pi Pico RP2040

Random numbers on RP2040
No purely software technique can produce truely random numbers. You need a physical source of input that is uncorrelated with the current program. For low rates, the input could be a human mouse click, or if there is an internet connection, maybe packet arrival time. The rp2040 has a high speed, ring oscillator clock (ROSC), which is not phase-locked to the system clock. The ring oscillator frequency depends on temperature, voltage, and process variations. The documentation suggests using the clock output bit as the input to a random number generator, but warns that the function is uncharacterized (see the datasheet, section 2.17). We wrote two different schemes to convert the random bits into useable 32-bit numbers:

By bumping up the ROSC frequency, using a Von Neumann extractor, and short software delays, we were able to generate reasonably distributed random numbers. The advantage of this scheme is that, aside from the ROSC bit, it uses only cpu time and no other hardware. The first example below uses this method.
The ROSC read, CRC32 computation, and C interface can be offloaded to three DMA channels. It is a little bulkier to set up, but is quite fast, assuming that you do not need to DMA channels for some other process. The second example below uses this method.

DISCLAIMER! The ROSC is not shown by the manufacturer or by me to have any reliable level of random generation. Further, of the three rp2040's I have tested, each gives a somewhat different oscillator speed, and different distributions of bits. Do not use this for any critical project without doing your own tests!

Software-driven, Uniform and normal distributed integer, bits, and s15x16 fixed point numbers.
The basic 32-bit unsigned int functions describled in more detail below were modified to produce two qualities of uniform 32-bit unsigned integers, fixed point uniform distribution between -1 and 1, fixed point normal distribution with mean zero and standard deviation of one, as well as three qualities of single bits. The lower quality routines are faster.

32-bit integer
- rand_rosc() returns a 32-bit unsigned int formed by reading the ROSC random bit 32 times and concantenating, then using the number as a seed for the rand funcion. The output of rand is returned.
- rand_rosc_VN() returns a 32-bit unsigned int formed by reading the ROSC random bit 32 times using a Von Neumann extractor, then using the number as a seed for the rand funcion. The output of rand is returned.
fixed s15x16 uniform -1 to 1
- uniform_rand() returns a s15x16 format fixed point number uniformly distributed between -1 and 1.
- If necessary the output is easily converted to a float for use or for better scaling behavior.
fixed s15x16 normal mean=0 SD=1
- s15x16 normal_rand() returns a s15x16 format fixed point number normally distributed with mean=0 and std.dev=1. In the linked image there is a red curve fit to a histogram of about 325,000 normally distributed events.
- If necessary the output is easily converted to a float for use or for better scaling behavior.
Three different single-bit generators that trade off speed for quality. In each of the linked images, the red dots represent the computed histogram distribution for about 15,000 events consisting of 20 coin tosses each.
- random_bit macro that returns a fast but somewhat correlated bit with value 0 or 1
- random_sign macro that returns a fast but somewhat correlated bit with value -1 or 1
- random_bit_VN() that returns single bit with value 0 or 1, decorrelated using a Von Neumann extractor
- random_bit_rand() that returns single bit with value 0 or 1, decorrelated using a call to rand_rosc() above

I wrote an application that allows you to play with the five random routines. At the command line you can specify generation of one of five distributions and specify how many events to allow. The event count is specified as 0 to 8. Each larger integer doubles the number of event. Zero corresponds to 400 events in the peak bin.
The distributions are specified as:

u -- a uniform distribution between -1 and 1 in s15x16 fixed point.
n -- a normal distribution with mean=0 and standard deviation=1.0 in s15x16 fixed point.
bl -- a binomial distribution simulating 20 coin tosses per event using the simplest, fastest, and possibily biased ROSC random bit.
bm -- a binomial distribution simulating 20 coin tosses per event using a Von Neumann extractor on the ROSC random bit.
bh -- a binomial distribution simulating 20 coin tosses per event using a 32 bit ROSC random integer as a seed for rand()&0x01.

Code, ZIP

DMA-driven, uniform, normal and one-bit integers.
The DMA channel sniffer can compute a CRC32 in one cycle on any value sent through it, using the initial value of the sniffer data register as a seed. The slower, software, integer routines from the last example are used once to generate an unpredictable seed, which is copied to the sniffer data register. One DMA sends the ROSC random bit through the sniffer. The next DMA block in the chain moves the sniffer data register to a C variable. The third DMA block in the chain moves a true to a C status vaiable indicating new data, then chains back to the first DMA channel. The three channel chain executes in about 120 nSec, or about 8 million random number calculations per sec But by the time that it is packaged and used in C you get 3 million/sec. The binomial distribution, normal distribution and serial correlation all look good, but again, no formal estimation of quality. The DLA program computes a Diffusion-limited Aggregation, shown below. The serial correlation program should generate completely random dot-field if everything is correct. The distributions program allows you to use the serial interface to plot binomial and normal distributions. The distributions shown have small red markers for the expected histogram shapes. The binomial represents events consisting of 20 coin tosses. The normal distribution is built up from 12 uniform, random integers..

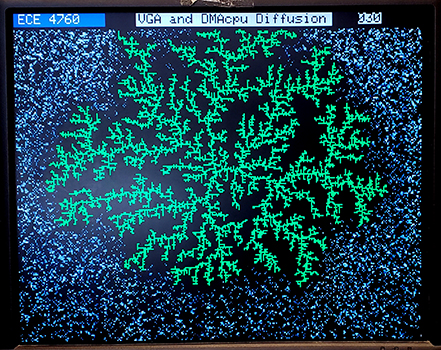
Code: DLA, serial correlation, distributions, ZIP

History; early steps in using ROSC

Uniform random 32-bit unsigned integers
The first thing to get running is a relatively unbiased 32-bit generator. There are two steps. First extract and concantenate 32 bits, then use this as a seed for the C rand function. The rand function served to scramble any remaining correlation between concantenated bits. The resulting distribution is displayed on VGA. I implemented two bit extractors, with different biases and speeds. One is simple and fast, but still shows some correlations. The second one is 5 times slower, but much less biased. The simple one is:

for(k=0;k<32;k++){    
      // at least one nop need to be here for longer timing  
      //extractor_count++ ;
      asm("nop") ; asm("nop") ; // adds one microsec to execution
      //
      random_bit1=0x00000001 & (*rnd_reg);
      random=(random << 1) | random_bit1 ;
    }

For each of 32 bits, wait for two machine cycles, which is more than 3 ROSC cycles at the ROSC frequency I chose, grab a bit from the rnd_reg and concantenate. A 32 bit random number is generated in about 6 uSec. The better extractor is:

for(k=0;k<32;k++){
      // von Neumann bit extractor         
      while(1){
        //extractor_count++ ;
        random_bit1=0x00000001 & (*rnd_reg);
        //  a small delay decorrelates the bits
        asm("nop") ; asm("nop") ;
        asm("nop") ; asm("nop") ;
        asm("nop") ; asm("nop") ;
        asm("nop") ; asm("nop") ;      
        random_bit2=0x00000001 & (*rnd_reg);
        // if the two are diferent, use the first one
        if(random_bit1!=random_bit2) break;
      }  
      // build the 32 bit sample
      random=(random << 1) | random_bit1 ;
    }

This code uses a Von Neumann extractor, plus a little delay, to produce an unbiased bit stream. Execution speed varies, depending on how may passes are required in the while loop, but is approximately 25-35 uSec. Each of the extractors is followed by a pass through the C rand function. As a sanity check, I computed and printed one generated number in main as soon as serial is enabled. The number is unpredictable, unlike the number returned from C rand. The speed of the ROSC is also printed. On my cpu the speed was 241 MHz with the speed range set to HIGH and full drive turned on in the freqA and freqB registers. You can try setting the speed range to TOOHIGH, but it may not work. My specific system gives 325 MHz on the TOOHIGH setting.

Code, ZIP

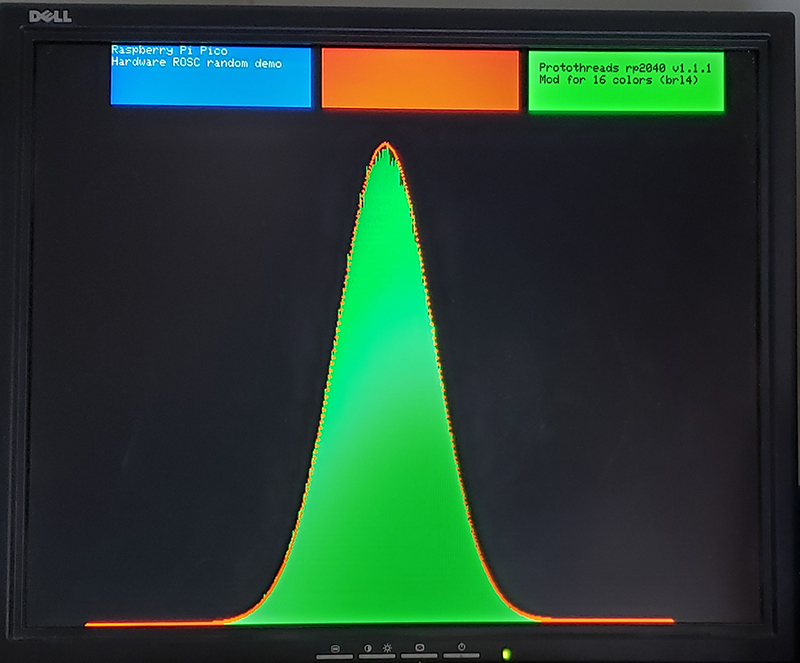
Normal distribution by adding uniformly distributed unsigned integers.
The Central Limit Theorem says that if you add together enough uniformly distributed numbers (UDN) that you must get a normal distribution. The Irwin-Hall distribution converges fairly closely to a normal distribution after adding about 12 UDN. The result of adding 12 UDN generated using the lower quality extractor is shown below. The samples are in green and the theoretical normal distribution is show in red. There is probably a slight deficit in samples near the peak. The deficit disappears if 20 UDN are used. For graphics or game use 12 is probably enough. Even 4 UDN added together has strong central tendency. In this code, the normal distribution is computed in the main loop and you can experiment with the effect of different sums of UDNs. (See the next project for better packaging).

Code, ZiP