Motion Estimation of Visual Stimuli

Introduction

Neurobiologists and people studying animal behavior often want to present visual stimuli to animals(1). Characterizing the motion of a stimulus for comparision with other stimuli is not well defined at present. We are attempting to figure out a scheme for measuring the strength or intensity of a motion sequence. The first application is in spider visual courting displays.

New material since this Journal Club presentation

Possible Methods

There are several ways of estimating motion. The two basic approaches are object based (e.g. 2) and image based methods. Object based methods use information about the 3D geometry of the structure generating the motion to estimate parameters such as joint rotation or limb velocity. Image based methods use only the information that might be available from a single video tape, or that might be observed by an animal under test. We chose to concentrate on image based methods because we need to compare video sequences as well as computer graphic models of spiders.

Two separate image based schemes were implemented:

• The first was based on optical flow computation between frames(3). This is based on the notion that pixel intensities only change from frame-to-frame because of motion. If true, and if I is the array of intensities at every point in a frame, and v is the vector velocity of the pixel then
  dI/dt = -grad(I) dot v
  or put in words the rate of change of intensity at a point is equal to the spatial gradient of the intensity dotted with the velocity. Solving for v gives,
  v = -(grad(I) dot (dI/dt))/mag(I)2
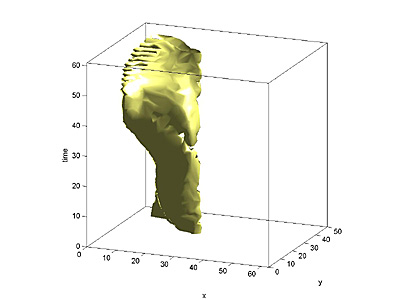
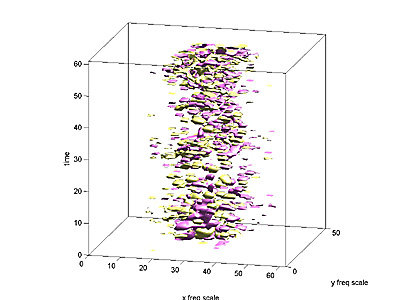
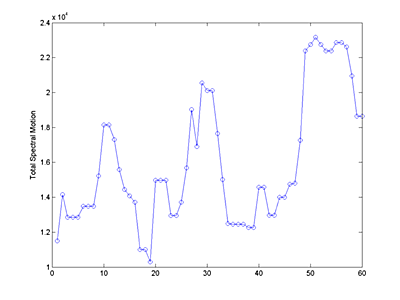
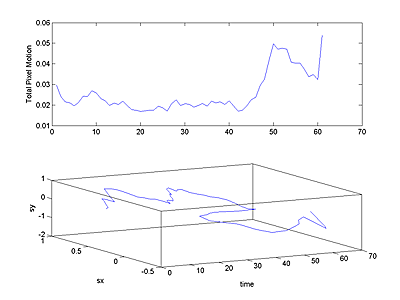
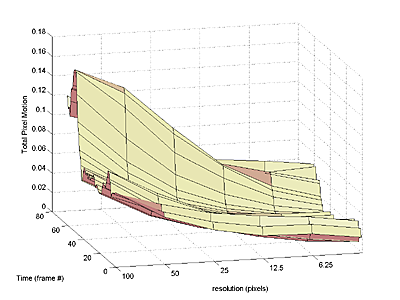
The resulting 3D speed field (2 space dimensions, plus time) was plotted as a volumetric isosurface. Also, for each frame, the total pixel motion was estimated by summing the speeds of all pixels. An estimate of the scale of the motion (size of the moving object) was made by repeating the calculation on downsampled versions of the image until only 4 to 8 (highly averaged) pixels were left in the image. Details of motion show in the early passes, but only large scale motion showed up in the final passes. The resulting surface of total pixel motion versus time and scale shows the size distribution of motion.
• The second was based on FFT phase difference measurements between frames. For each frame, the 2D FFT was computed. The phase of each different frequency component was converted to a time by dividing by the frequency value. Normalizing to a time caused each harmonic of a spatial structure to have the same value. A motion strength was then computed for each frequency component as the diffenence in time between successive frames, times the amplitude of the FFT at that frequency. The justification is that weak intensities don't carry much information, but if they are moving fast, they might be important, whereas high intensities indicate high contrast objects. The total motion was computed as the sum of the motion strength of all the frequencies, except for a few near DC.

The programs

The following matlab programs implemented the various features noted above. In all cases a slightly downsampled version of the animation was used for analysis.

• The first example takes as input (download this with a save target as...) an image sequence (an animated spider) and produces an isosurface of which pixels moved the most, the total pixel motion at each time, and a 3D trajectory plot of [speed in x direction, speed in y direction, and time]. The three figures resulting from the calculation are shown below. The increase in speed of the whole length of the arm is clearly visible around frame 50.
  
• The next example uses the same input sequence but implements the multiscale analysis to show pixel motion at different scales. The figure below shows motion versus frame number (into figure) and resolution (right-to-left). At the right edge, the figure only has about 6 pixels, so that only the biggest motions will contribute to the surface altitude. The break point at which the surface starts to drop is determined by the size of the moving object in pixel units. The high peak toward the left-rear represents the down stroke of the long leg segment. A lot of pixels are moving fast, so the surface is high, but drops off to the right as the leg is averaged into the still image.
  
• The third example uses the same input sequence but implements the FFT analysis. The two figures show a volumetric view of the frequency components (1/scale) with the largest motion strength and the total spectral motion. Clearly, understanding the volumetric display is going to take more work.
  

References

1. Jacky Dragon ref
2. Agrawala M, et.al., Model-based motion estimation for synthetic animations, http://www-graphics.stanford.edu/ and ACM Multimedia 1995
3. Beauchemin SS and Barron JL, The Computation of optical Flow, ACM Computing Surveys, Vol 27, No 3, pp 433-467, 1995