Introduction
Was that a ... projectile? a rocket? an [XXXXX] missile? That was a dynamically controlled parachute guidance system looking for its target.
The purpose of this project was to design a dynamically controlled parachute guidance system using an Atmel ATmega32 microcontroller. A set of avionic hardware was built and software programmed in addition to the medium-sized model rocket launch vehicle. For this project, we tried to demonstrate an affordable guidance control system that carried and landed a scientific payload at a targeted site. To achieve this task we built a rocket and attached the microcontroller to a series of sensors to obtain flight data. The sensor data determined where the rocket is at all times (and was responsible for setting off the ejection charge for the parachute at apogee). After the custom-made steerable parachute is opened, two stepper motors were used to guide the rocket to its destination (where it started).
Background
For the past couple decades, an investment have been placed into researching and developing various parachuting control systems to improve the accuracy for cargo drops. Cargo parachutes often used by the military and humanitarian organizations to deliver payloads such as food, ammunition, and equipment are essentially un-steerable. Once the cargo is released from the aircraft, there is no way to control its flight path, which is highly dependent on various atmospheric conditions. The defense agencies and space programs have been trying to construct unmanned cargo parachutes control systems that are both affordable and highly accurate for its scientific payloads. These systems often use GPS receivers, magnetic compasses, navigational sensors, IMUs, and RF tracking systems along with parachutes, pryos, inflatable airbags, and/or aerodynamic gliding designs.
Methodology
Through the use of accelerometers and gyroscopes, we were able to determine the delivery system's acceleration, velocity, positioning, and angular velocity, which were calculated in live-time by the microcontroller. We used three 1-axis 8-g high-precision accelerometers (sampled from Freescale) and a 150 degree/s rate gyro (sampled from Analog Devices). The accelerometers was used determine to the xyz accelerations relative to the current position of the rocket. The rate gyro provided us the angular velocity. With these four sensors, we were able to determine our true location and heading. The rotation with respect to pitch and roll were considered insignificant, which added little value, but great complexity to implement. The steering is done by two stepper motors, which controls the canopies of the custom-made steerable parachute. The steering is similar to a sky-divers controlling a ram-air parafoil parachute by togging the left and right canopies to spin and turn, in order to get to the desired landing site. The stepper motors will use the feedback from the navigation control system to control the direction of the payload. Upon landing the data was extracted from the EEPROM of the microcontroller and analyzed using MATLAB.
The Math and Science Behind Everything
From the physics aspect, the dynamics of parachutes that affect the guidance and control is a two body system connected by suspension lines. Although the parachute weight may be small in terms of physical material and payload weight, it actually acts like it had a much bigger mass by virtue of the unsteady aerodynamic "apparent-mass and inertia terms." (AIAA document, PV1995-1537).
A simplified ram-air chute was used for this project. Complicated ram-air parachutes are used for parachuting by sky divers. The rectangular shape with flipping canopies gives it great horizontal control. There is no vertical control (solely depended on gravity and wind). All ram-air chutes are designed to flare by "stalling" at large toggle inputs. If these input levels are held, pitching oscillations will often build up. Figure 1 shows a typical ram-air steerable parachute with the model axes and forces defined. There are various off the shelf commercial software that can calculate the six degree-of-freedom right body-axis model.
Computing the formula for this dynamic feedback control system was way too hard to do. There are simply too many variables (coefficient of drag, center of gravity, center of pressure, the servo response as a function of torque, the current velocity, the current tilt in the parachute, etc.). However, since we have the live data and the memory capability to track the system from launch off, we can constantly update our present position and headings. The data that we have are acceleration in the x, y, and z axis along with the angular velocity around the z-axis. The relative velocity and position can be obtained through integration. The true acceleration, velocity, and position are obtained through a rotation translation using matrix algebra.
For a typical launch, the initial values while sitting on the launch pad will be 0g for the x and y axis, -1g for the z-axis, and 0 angular velocity. Prior to every launch, all sensors were re-calibrated. Once the rocket was launched, the z-axis acceleration was updated along with it's integration dependent z-velocity and z-positioning. Minimal changes in the x, y, and angular velocity were expected during the launch process. When the z-velocity transitioned from positive to negative, the ejection charge was fired (assuming all the safety inhibit conditions were met). Once the parachute popped out, the z-axis acceleration, velocity, and positioning becomes neglected, since there are minimal controls over the descent rate. The true x and y values are obtained after a rotation translation using the rate gyro. (see Software section for calculation algorithms - see verelet section)
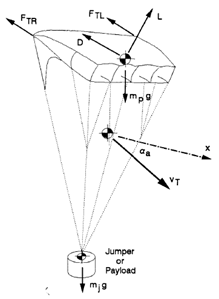
Parachute Simulation Force Model
Two stepper motors were used for controlling the descent phase. Each motor controlled one of the canopies. Using the stepper control algorithm (see Software section), the stepper motor will yank on one of the canopies by tightening and releasing the motor. The yanked motor will act as the pivot for the spin motion. Therefore by yanking, the heading was consistently adjusted, steering towards the targeted landing site.
Societal Impact
The rocket to be built met the FAA and NAR regulation. The rocket for this project did not weigh more than 1,500 grams (53 ounces) at liftoff and will not contain more than 125 grams (4.4 ounces) of propellant or 320 N-sec (71.9 pound-seconds) of total impulse. Table 1 show the required field dimensions for each class of motor engine used.
|
LAUNCH SITE DIMENSIONS |
||
|
Installed Total Impulse (N-sec) |
Equivalent Motor Type |
Minimum Site Dimensions (ft.) |
|
0.00--1.25 |
1/4A, 1/2A |
50 |
|
1.26--2.50 |
A |
100 |
|
2.51--5.00 |
B |
200 |
|
5.01--10.00 |
C |
400 |
|
10.01--20.00 |
D |
500 |
|
20.01--40.00 |
E |
1,000 |
|
40.01--80.00 |
F |
1,000 |
|
80.01--160.00 |
G |
1,000 |
Lanuch Site Dimension Requirement, from NAR Regulations and Rules Document
For the demo, all of the above parameters were met. The rocket used was 52 ounces and the total impulse of for Estes E9 engine was 121.7 Ns. This project abided by all Federal Aviation Administration (FAA) laws governing the use of airspace and any other federal laws related to the use of airspace, combustible/flammable material, safety codes, guidelines, and procedures for building, testing, and flying the model rockets. The procedures and safety regulations of the Bureau of Alcohol, Tobacco, and Firearms and Explosives (BATF) and the National Association of Rocketry (NAR) were used for flight design an operations.
Though there were certain environmental concerns with building a rocket which includes the effects of the fumes of the different chemicals that we will use (epoxy, fiberglass, spray paint, etc.); however, all phases of the rocketry construction were completed at an off-campus site that meets all the proper ventilation requirements. All construction completed in the lab was electrical.
The launch rod was built with a ¼” rail guide and the launch station will be located more than 50 feet away from the launch pad.
This project does have several safety concerns; however, there are many mitigation steps that will have implemented to reduce the risk to minimal. As for legal considerations, we derived most of the code on our own, modified old project versions, or obtained from sites with general public license. Since there was no RF that is being used in this project, thus no FCC regulations need to be taken into account. In addition, we followed are Cornell regulations and building codes when we do our drop test in Duffield 340.
Tradeoffs
There were several things removed from our system since the proposal as tradeoff. Due to a limiting budget, we did not obtain the original servos; however, with the proper gears, we were able to obtain a workable amount torque with stepper motors to control the parachute.
The original intent was to use a +/-8g accelerometer for the z-axis and a low-g high-precision 3-axis accelerometer so that we can have a very high accuracy. Because the high cost of these high-precision 3-axis accelerometers, we were limited by the available samples. Of the samples available, we were only able to obtain those of the LGA or QFN package. Part of the reason was that we had difficulty pin soldering to a LGA-14 package with 32 gauge wire. We may have shorted input/outputs for 2 of the 5 accelerometers soldered (because it overheated when we connected it); and the other 3 accelerometers did not provide reasonable data.
Due to the potential inaccuracy, we intended on obtaining a barometric sensor to verify the altitude data; however, due to the time restraint, we were never able to build and test the hardware for it.
We decided to use a more complex software algorithm and use an external ADC in order to have less noise than the internal ADC. Originally, 12-bit ADCs were supposed to be used; however, we were not able to get the 12-bit SPI ADCs sampled from Texas Instrument to work with our system; however, we were able to get the 8-bit ADC to work. We later ordered 12-bit ADCs from National Semiconductor of the same series. The time restriction prevent us to go through all the phases of “Test Like You Fly” philosophy, we stuck with the 8-bit ADCs, losing some precision on our data calculations.
A drogue parachute would be particular help for the operation. However, because the hardware cannot handle a 180 degree flip (pitch) when the main chute pops out, the drogue parachute is removed from the system. A 180 degree flip would me inverted all the axis in our calculations and the rate gyro is rated at only 150 degree/s. Without a drogue chute, there is the risk of high speed main parachute ejection which can lead to tearing the parachute or tangling of the cords. In addition, there is only one parachute, thus a single point failure which we lead to the loss of all avionics if the rocket indeed comes down ballistically in the case of no ejection (see recovery system for the risk mitigation). When there is no drogue chute, the main parachute was moved to the upper stage, resulting in a less stable rocket. The length of the rocket was adjusted to compensate for this to some degree.
|
Original Design |
Final Design |
Tradeoff |
|
LIS3LV02DL |
MMA1220D |
Loss of
accuracy |
|
ADC128S022CIMT |
8-bit
accelerometer |
Loss of
accuracy |
|
Barometric
Sensor |
|
Loss of
secondary altitude determination |
|
Servo Motor |
Stepper
Motor |
Loss of
torque (with the restricted gear configuration) |
|
SD Card |
EEProm |
Less data
recorded |
|
Drogue &
Main Parachute |
Main
Parachute |
Single
parachute - high speed main parachute ejection (risk of
tearing), no backup parachute (ballistic recovery – loss of all
avionics hardware), and less stability (main chute have to be
placed in the upper stage. |

The Rocket Demo Launch
Related Resources

Joseph N. Pew Engineering Quad/Duffield (the overhanging room): Site of the inital drop test

