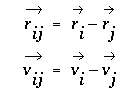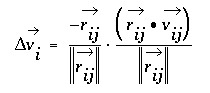ECE 4760: Laboratory 2

Video Game -- Particle Beam

Introduction.

You will produce a game in which ball-like particles enter from one side of the screen. The paddle position will be controlled by an analog input to catch balls. There will be a time limit to the game. Display will be on an 320x240 TFT LCD, with DMA sound effects. The balls will follow standard billards-type dynamics, with zero friction between balls. An example of billard dynamics is shown below. The sound must be produced through a DAC output using a DMA channel.

Procedure:

In this lab and every lab, make sure you are running Protothreads 1_2_2 or later.
There is a fixed point animation example on the Dev Board page, including forces for gravity and drag (video).
All TFT connections from lab 2 stay the same and are wired for you on the big board.
Most of the DAC connections stay the same, except as noted below.

Sound effects using DMA SPI:
The SPI DAC you will use is the MCP4822 as in Lab 2. But you will be using DMA to drive the SPI channel, so you need to modify the chip-select pin on SPI2 to use framed SPI. This mode allows the SPI controller to toggle the chip select line, implying that only one peripherial can be attached to that channel, but simplfying program logic. See section 23.3.6 in the reference manual. Specifically, this feature allows a DMA channel to blast data out to a DAC or other fast device without using an ISR. Get sound output by connecting the DAC output (DACA or DACB) to the speakers.
DMA setup:

Game Controller via ADC:
ADC input AN11 pin 24 using the potentiometer circuit shown below.

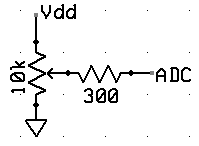
The game will be controlled by a trimpot potentiometer hooked to an ADC input on the PIC32. Use the circuit to the left to make a user-variable voltage. The Development Board page shows how to set up the A/D converter to read a voltage in a thread. The example reads the AN11 analog input and draws the voltage on the TFT.

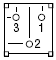Trimpot schematic:trimpot bottom view: trimpot image: trimpot



Fixed Point arithmetic

Floating point is too slow for animation, so you will be using a fixed point data type and doing all arithmetic in fixed point.
The animation example linked above uses the _Accum data type.
To generate a random number in fixed format:
static _Accum Accum_rand, Accum_rand_scaled ;
// fraction from 0 to 1
Accum_rand = (_Accum)(rand() & 0xffff)>>16 ;
// range from -2 to 2
Accum_rand_scaled = ((_Accum)(rand() & 0xffff)>>14) - 2 ;
// to print
sprintf(buffer,"%f", (float)Accum_rand_scaled);

Frame rate

Set the TFT frame time using a thread to be faster than 15/second.
Since the computation will be the most demanding calculation and depends on the number of balls,
arrange the thread to produce a constant frame rate, while allowing as much time as possible for computation.
(pseudocode example of constant frame rate)

Dynamics:

You are going to be programming in the equations of motion for the balls. Remember that the video coordinate system has x increasing to the right and y increasing downward. We will step the billards system forward in time by calculating the total change in velocity from a collision, without worrying exactly how forces change the velocity.

The change in velocity during impact can be derived for frictionless balls of equal mass by noting that the the impact force must act in a direction parallel to the line connecting the centers of the two impacting balls. The change in velocity must be parallel to the connecting line also, with the velocity component parallel to the line having its sign reversed by the collision and the velocity component perpendicular to the line unchanged. Projecting the initial velocity onto the line connecting the centers, negating the result, and resolving it back into x and y velocity components gives the velocity change. If i and j are the indices of the colliding balls, define:

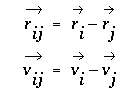
then delta v for ball i is given by the following where the right-most term represents the projection of the velocity onto the line and the other term converts the projection back to x,y coordinates.

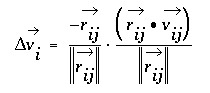
The calculation procedure for each time step is:

  1. Compute the Δv for each collision, based on the positions of the balls, and add it to the current velocity. Do this for every pair of balls. This step is time consuming, but only has to be performed for any two balls if they are less than 2 radii apart. Ball-ball collisions will not be exact because of finite time steps. One consequence of this is that balls tend to capture each other when they collide. You will need to do a numerical hack to avoid capture. I suggest that after a ball collides with another ball or the paddle, that it not be allowed to collide again for a few frames. For collision debugging, it will be useful to slow down particles to less than one pixel/frame.
    Pseudocode for this might be:
    For each ball i from 1 to n
      For each ball j from i+1 to n
        Compute approximate rij by checking:
        if Δx and Δy are both less than 4
         if (||rij||2 less than (2*(ballRadius))2 and hitCounteri is zero)
            Compute vij
            Compute Δvi
            Add Δvi to vi
            Subtract Δvi from vj
            Set hitCounteri big enough to avoid particle capture
         elseif (hitCounteri>0)
            decrement hitCounteri
         endif
        endif
      endfor
    endfor
  2. Using _Accum fixed point, any Δx or Δy greater than 256 (sqrt(65535)) will overflow when squared and produce erratic results.
    This means that BEFORE you square the deltas, you should do the very quick check to see if both deltas are less than 2 ball radii.
  3. When I coded this, I did not bother to calculate the square root of the sum of squares when calculating ||rij|| (too slow).
    Compare the squares.
  4. When dividing by ||rij||2 you need to be careful not to divide by zero (causes reset). A low ||rij||2 implies a head-on collision,
    so if ||rij||2 <1, just switch the velocities of the two balls. Otherwise, do the divide, perhaps by table-lookup.
  5. For each ball (and after the Δvi from any collision is applied for that ball), simulate friction between the ball and table by making
    vx(t+dt)=vx(t)-vx*drag and vy(t+dt)=vy-vy*drag
    The drag should be small, perhaps drag=0.001 ( but converted to fixed notation).
  6. Update the positions according to
    x(t+dt)=x(t)+vx*dt and y(t+dt)=y(t)+vy*dt
  7. Detect collisions with the walls and modify velocities by negating the velocity component perprendicular to the wall.
  8. Delete any balls which are collected, or which make it past the collector to the left side of the screen, and modify the score

Clearly, v and x all need initial conditions, which you will set, according the specifications below. It is doubtful that you will have enough time between frames to do all of the calculations in floating point. I suggest using 32 bit, signed numbers with the binary point set at the 16-bit boundary. I also suggest scaling velocity so that you can make dt=1, thereby avoiding a multiply. You can think of this as:
(1) Units of distance are PIXELS,
(2) Units of velocity are PIXELS/FRAME.

The previous analysis is adapted from: Studies in Molecular Dynamics. I. General Method, by B. Alder and T. Wainwright,
Journal of Chemical Physics, Vol 31 #2, Aug 1959, pp 459-466. See also Hard-Sphere molecular dynamics.

Results:
2016: video On TFT

Week one required checkpoint

By the end of lab session in week one of the lab you must have TWO of the following:

Week two required checkpoint

By the end of lab session in week two of the lab you must have ALL of the following:

Week three Assignment

Write a program in C using ProtoThreads with these specifications:

When you demonstrate the program to a staff member, you should play the game.
At no time during the demo should you need to press RESET.

Your written lab report should include the sections mentioned in the policy page, and :

Copyright Cornell University
September 30, 2019
sent with 100% recycled electrons.