ECE5760 Final Project

 Adaptive Noise Cancellation

FPGA Implementation
 
Contact Information:

 

Jinda Cui
Jiawei Yang

 

 

 

 

 
 

   

Figure.2 Detail structure of the DE2 hardware design
Figure.3  LMS state machine
Figure.4: VGA display state machine

 

Figure 3 is the detailed description of the LMS state machine. For simplicity a four weight adaptive filter is illustrated here. The weight update starts at the rising edge of the AUDIO_DACLR clock and is executed only once in one audio cycle. To reduce the usage of fixed point multipliers, a simplified version of LMS algorithm is used for this noise canceller which replaces mu, the stepsize, with a shifting operation and the multiplication of the reference noise sample with its sign bit. This simplified weights update scheme does not require any multiplications in the state machine and efficiently helps reduce both the complexity of the algorithm and the usage of logic elements. Since LMS algorithm involves recursive computation of each filter weight, a circular buffer is needed to update the current reference noise data. As shown in Figure 4, the noise history update is realzied by increasing the base pointer by one each time the weights are updated. The maximum value of the base pointer must be equal to the length of the memory buffer and greater than the number of filter weights so that it won't disrrupt the previous noise samples when it overflows.

 

 

Figure 2 shows the top level block diagram of the hardware adaptive noise canceller. The stereo line input consists of two different input signal: the corrupted source in the left channel, and the reference noise in the right channel. As discussed in the the Theory Highlight section, the reference noise, together with the estimated filter output and the stepsize mu, determines the how fast the wenights are updated. The weight updates are defined in the LMS state machine which runs and processes one audio sample during one audio cycle. In addition, another state machine is instantiated to display all the filter weights on a VGA monitor for observation purposese.

Figure. 1 Structure of  hardware implementation of adaptive noise canceller

 

 

 

    

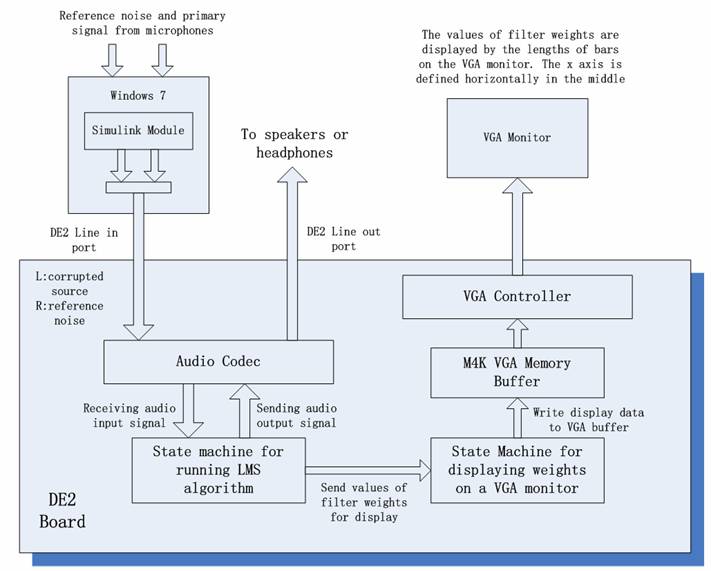
The detailed structure of the adaptive noise canceller is shown in Figure 1. In order to perform blind filtering, the adaptive filter requires the measurements of the reference noise and the primary input signal, which is the desired source signal contaminated with the noise. The noise can be effectively used as the reference only if it is measured in a field where the source is relatively weak. Therefore, the microphone that records the reference noise must stay a certain distance away from the one that records the primary input. The two speakers that play the noise must be the same set so that the noise is sychronized everywhere in the measuring field. Since a typical desktop usually has only one mic input, two audio-to-mic USB adaptors are used to receive both the reference noise and the primary input synchronously. For real time data acquisition and adaptive filtering, the inputs are recorded, concatenated and played back as a stereo output signal, which then serves as the input to the FPGA. This structure also allows asynchronous adaptive filtering, which means that the input data can be recorded, stored in MATLAB workspace, and used as the input to FPGA for adaptive filtering later. In addition, a VGA monitor is used to display the values of adaptive filter weights so that we will be able to watch the convergence behavior of the adaptive noise canceller.

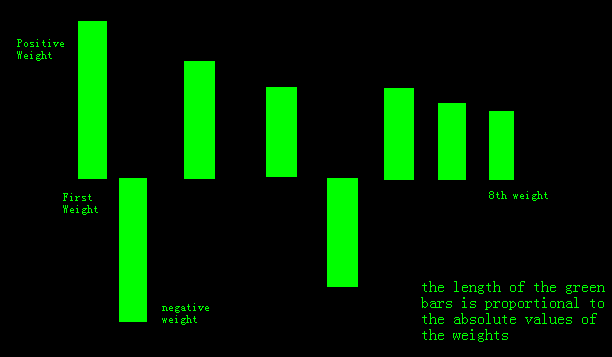
Figure 5: Weight display scheme

The state machine that implements the filter weights display is shown in Figure 4. The weights are displayed in terms of its magnitude and sign bit. The state machine starts with the initialization of an iterator (the walker). The state machine will check the current x axis coordinate of the iterator and decide which weight this point belongs to. Once the weight target is determined, the state machine will then check the sign bit of the weight and negate the weight if sign(w)==1. Next the state machine will check the current y axis coordinate and if the iterator is in the predefined weight range the state machine writes one to the M4K buffer at the current address. Otherwise, the state machine writes zero to the M4K buffer. In the end, the state machine updates the iterator and enters the next cycle. Figure 5 is the visual illustration of the weight display scheme.
 
 
  

 

 
©2011 The School of Electrical and Computer Engineering, Cornell University