HPP Model
The HPP model is a form of cellular automaton. It is “a collection of colored cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules based on the states of neighboring cells.” (from Wolfram MathWorld) The system will keep evolving indefinitely because energy never travels out of the system, unless the boundary conditions are set to allow this. In our implementation, we modeled the system on a two-dimensional square grid, with particles capable of moving to any of the four adjacent grid points sharing a common edge but not diagonally.
Mathematical Background
In the HPP model, each particle has an associated direction and each lattice grid cell can only contain a maximum of one particle for each of the four directions. Therefore, the particles in a grid cell can be modeled by the 16 states below.
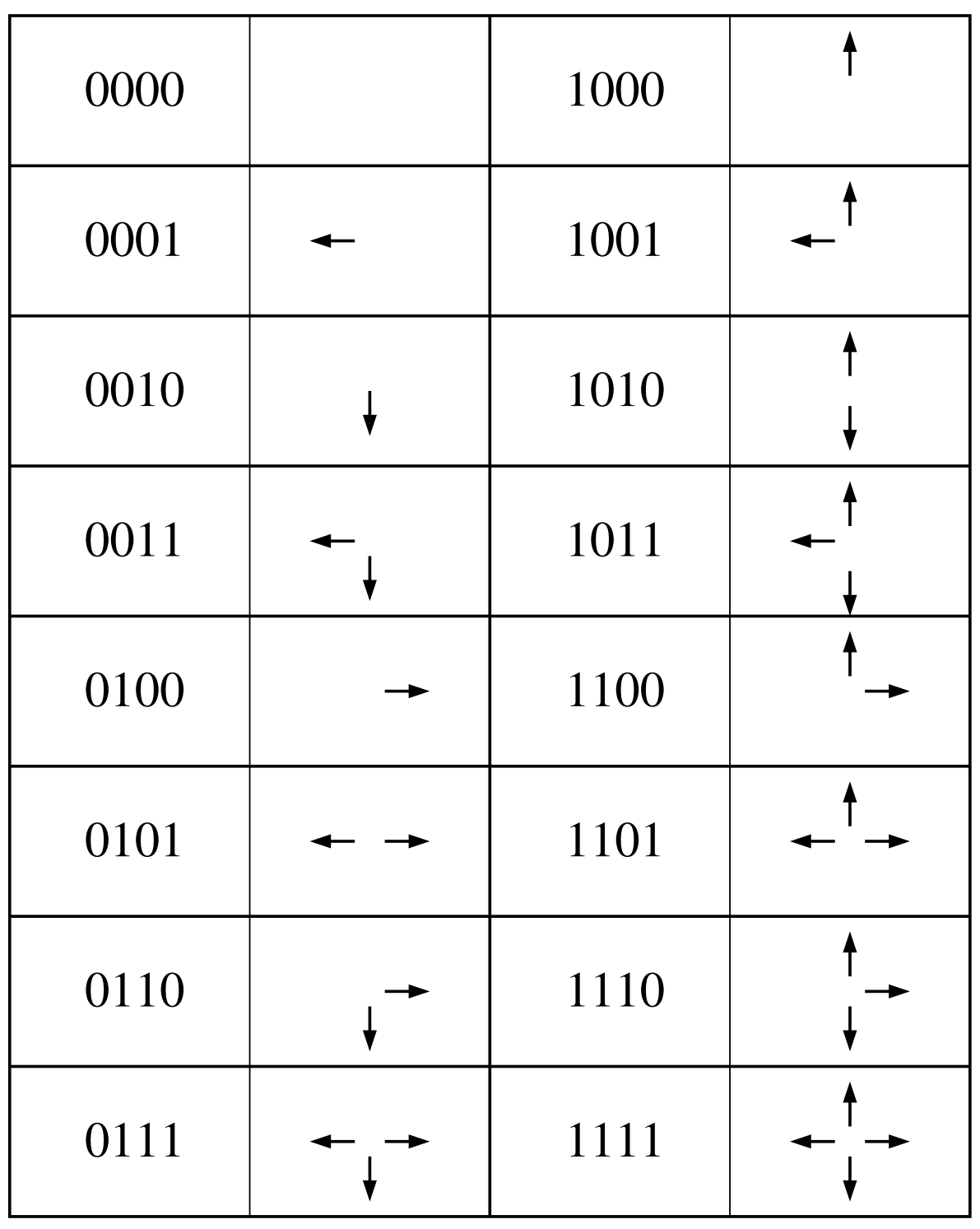
The following rules govern the movements of the particles and the collisions between them: (Source Wikipedia)
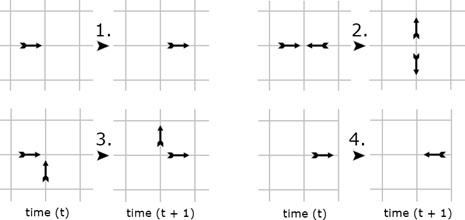
- A single particle moves in a fixed direction until it experiences a collision.
- Two particles experiencing a head-on collision are deflected perpendicularly.
- Two particles experience a collision which isn't head-on pass through each other and continue in the same direction.
- A particle rebounds when it collides with the edges of a lattice or an obstacle.
Overall Design Strategy
The specifications of HPP model lends itself extremely well to parallelization. The states of the grid cells are mostly independent from each other, and the evolution of a grid cell only depends on the state of itself and the four adjacent cells at the previous timestep. While parallelizing all the cells on the scale of a VGA screen would require too much hardware resources, a combination of parallelization through hardware-implemented processing elements in one dimension (e.g., y or vertical) and serialization through memory sharing in the other would be an intuitive approach.