ECE 5760: Laboratory 2

Hardware ODE solver with Nios II control.

For this exercise, you will simulate an analog system using a Digital Differential Analyzer (DDA) and control the function of the circuit with a NiosII cpu. The positions of the two particles will be plotted as a function of time on the VGA display. You can consider the DDA as a special purpose, reconfigurable, calculator controlled by the NioII.

Read the DDA page. After reading the page introduction, the example code that you want to use is at the end of the page.
The physical system you will simulate is the coupled, spring-mass system shown below.
The image is modified from a paper by Alex Gagen and Sean Larson.

The differential equations for this system are:

m(d2x1/dt2) + k1(x1) − kmid(x2 − x1) + D1(dx1/dt) = 0
m(d2x2/dt2) - k2(x2) + kmid(x2 − x1) + D2(dx2/dt) = 0

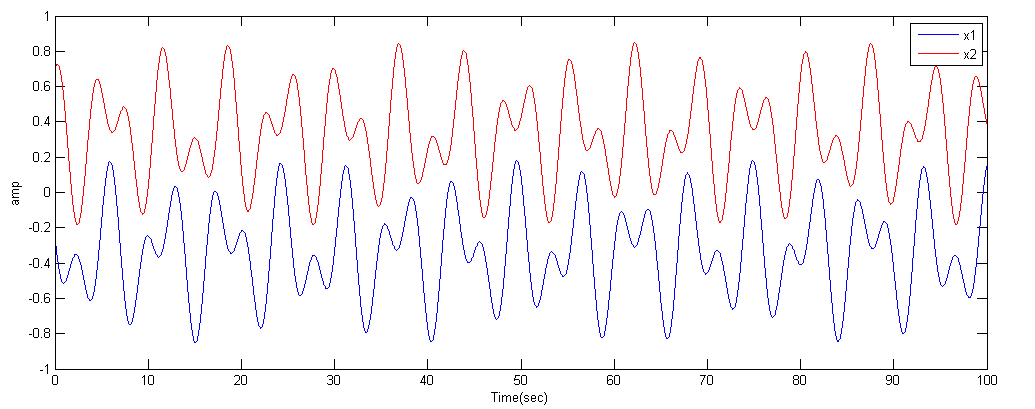
The k's are spring constants, m the mass, and D's the damping coefficients. The outputs are x₁ and x₂ which will depend on position and velocity initial condtions, as well as the equation constants. A matlab code and function provides a reference solution, to which you will compare your solutions. The image below is a typical output from the matlab program.
Note that the matlab code includes cubic force terms for the springs:
spring_force1 = k1 * ((x(1)-left_wall) + k13*(x(1)-left_wall)^3)
You will have to add one such term (k13) in the assignment below.

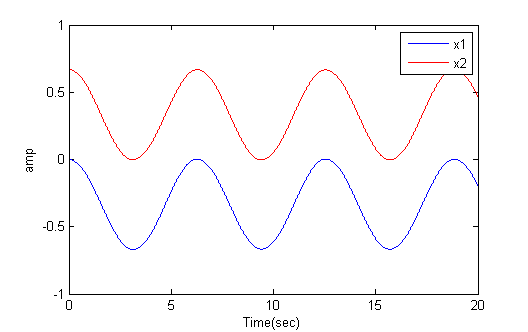
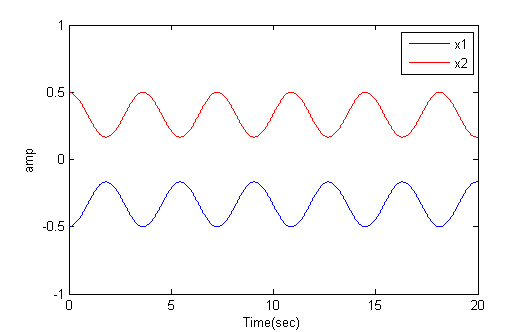
But in general the solutions are linear combinations of symmetric and antisymmetric solutions. The anti-symmetric solution corresponds to masses moving in exactly the same directions at all times, so that the center spring stays at its rest length, R. If the two outer springs have equal k and rest length L, then at rest, k*L=kmid*R and 2*L+R=2. For example, if kmid=k then the distance betweent the two masses can stay at separation 0.67 indefinitely (first image below). If the two masses are started at symmetric positions (relative to zero), then they move in opposite directions at all times (second image).

The previous matlab program uses the high performance ode45 solver. On the FPGA you are going to be using simple Euler integration.
This matlab program is coded to use Euler integration so that you can directly compare the the FPGA solution. The undamped solution is unstable, so a little damping is added.

-- NiosII See also:

There are now three different versions of Quartus used in the lab.
You may need to search the Altera site for the tutorial corresponding to the version you decide to use.

• VGA for NiosII -- Use notes for 640x480 resolution
• Signal Tap logic analyser tutorial (on chip)
• Intro to SOPC builder
• Qsys tutorial (version 13 and up)
• Using SDRAM
• NiosII introduction
• Altera Monitor Program
• HAL in Altera Monitor
• NiosII Literature
• NiosII hardware tutorial
• Nios Software handbook.
• Embedded Peripheral Users Guide
• Incremental compilation for QuartusII

--Setting up Altera Monitor System

1. Altera monitor is installed on the lab computers. On your own computer, download the executable from Altera
   Make sure that you choose the version that matches the version of QuartusII which you decide to use.
2. Install the executable. You will not be able to run it unless you ave previously installed QuartusII and the NiosIDE tools (for the same version).
3. When you run the monitor program in the lab, it may tell you that QuartusII is not installed. If so, open control panel>system>advanced>environment variables and add a variable with name QUARTUS_ROOTDIR and value c:\altera\11.0\quartus.
4. Follow the directions for setting up a new project in Altera Monitor Program. Choose the C option which uses program with device driver support.
5. If you get the following message when downloading your program to the NiosII (when using SDRAM for the program):
   

   Using cable "USB-Blaster [USB-0]", device 1, instance 0x00
   Pausing target processor: not responding.
   Resetting and trying again: FAILED
   Leaving target processor paused> 

   Then some suspects come to mind:
   1. You forgot to assign pins to the QuartusII project.
   2. There is an incorrect or missing PLL file for SDRAM delay (use the megawizard to rebuild or generate a new PLL module as described in the SDRAM tutorial.) Special Note: The component altpll has changed between release 7 and 8 of Quartus. When defining a PLL for the phase-shifted SDRAM clock c0 (as explained in the SDRAM tutorial), you need to add an c1 output to the PLL with zero phase-shift and use this signal for the NiosII clock! If you don't do this, the program will load normally, with no error messages, but the program will not run! A new, corrected project is zipped here.
   3. There is a misspelled control line in the Nios module interface, usually the clock or reset signal.
   4. The reset line is being held low/high by incorrect logic.
      Using reset=~KEY[0] will kill the processor! Whereas using reset=KEY[0] is fine.
   5. Check the size of the compiled hardware design. If the size is less than about 2000 logic blocks, then the Nios was probably optimized away. Check all the warnings to make sure no NiosII registers were reduced.

--Using QuartusII SignalTap tool to verify your design.

From the Altera Tutorial: The SignalTap II Embedded Logic Analyzer is a system-level debugging tool that captures and displays signals in circuits designed
for implementation in Altera’s FPGAs. SignalTap II can be used to capture and display signals in real time in any FPGA design (some M4K blocks are used).
You can:

• Probe signals using the SignalTap software.
• Set up triggers to specify when data is to be captured.
• Configure Sample Depth and Buffer Acquisition Modes using on-chip memory.
• Configure QuartusII to keep registers which are otherwise optimized away.
  

Example from 2016 by Tahmid Mahbub, Manish Patel, Matt Filipek

1. Build a DDA which simulates a coupled spring-mass system as described above.
   -- Choose the spring constants, masses, and time step so that the natural frequencies of the system are around 500 Hz.
   -- Scale the amplitude so that the integrators stay in range (+/-1).
   -- Scale time so that the spring constants stay in range (+/-1).
   -- You can set the mass to a constant m=1 .
2. Monitor the two position variables using a VGA output of x₁ and x₂ versus time.
   -- The display should look much like the matlab plot above.
   -- Scale the display so that the amplitude range takes up about one half of the VGA vertical resolution.
   -- The horiziontal VGA coordinate should be in integrator time steps (or a small multiple of the time step) so as to show a few cycles.
   -- The display should be erased when a new simulation starts. It should freeze when the simulation stops.
3. Build a NioII cpu and program it to allow an operator to use a serial console to:
   -- Set the four initial conditions of the simulation.
   -- Set the three linear spring constants.
   -- Start/Stop the simulation.
   -- Turn on/off a cubic spring term for spring 1 with a value of about the same as the linear term.

Be prepared to demo your design to your TA in lab. You will be expected to show:
-- Set arbitrrary initial conditions and all three spring constants
-- Symmetric and antisymmetric modes with and without the cubic spring term.

Your written lab report should include:

• Mathematical considerations (type of integrator, error expected/measured, approximations)
• screen shots of the VGA
• How you implemented the DDA circuits.
• A heavily commented listing of your Verilog design and GCC code.