Digital Filters 101

Central to the spectrum analyzer are the various bandpass filters at the different critical frequencies which process samples of input signals. Assuming a A/D module (which, in our case, was supplied by the AT90S8535 microcontroller), we basically had to implement the various filters for signal processing.

Infinite Impulse Response Filters

Essentially, we constructed the filters from the following, generic transfer function:

Note that the above transfer function implements an Infinite Impulse Response filter. Basically, an IIR filter takes as inputs previous outputs as well as current and previous inputs to produce the current, filtered output. Hence, a feedback loop is present. The above transfer function transforms, in the time domain, to a difference equation. The 'a's and 'b's in the above transfer function translate to the coefficients of the various terms in the difference equation. As we can see from the above, H(z) gives an expression for an n-th order filter.

Values for a and b above can be determined from computing the poles of the above transfer function.

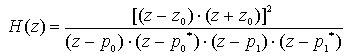
p₀ and p₁ are the poles of this 2nd order band-pass filter while the z's represent the zeroes. '*' denotes complex conjugation. Hence, a two pole filter with nonzero a coefficient values and 3 b values can be formed by expanding the denominator and numerator respectively of the above equation. The poles p are of the form

where A is the magnitude and theta is the angle made by the whole in the unit circle z = 1 in the complex plane. Poles p were calculated based on the following relationship:

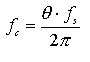
where f_s is the sampling frequency of the system - 9 kHz in our case. f_c is the desired critical frequency.

Finite Impulse Response (FIR) Filters

FIR filters were the most prevalent aspect of our design. Basically, FIR transfer functions derive from impulse responses that are finite in duration. FIR filters exhibit several properties, namely:

The phase response can be made linear, i.e. FIR filters exhibit Generalized Linear Phase whereas IIR filters do not. Linear phase provides less phase distortion (and is thus more manageable) than non-linear phase.
The impulse response exhibits symmetry about the midpoint, thus simplifying computation requirements.

The transfer function of an FIR filter transforms, in the time domain, to a difference equation that depends only on the current and previous input values. Hence, feedback is not present in the construction of FIR filters. This further simplifies computation. Essentially, the FIR filter transfer function gives rise to the following:

where the b values are the respective coefficients in front of n (thus, an n-th order FIR filter) input samples.

FIR filters also have the property that they are not prone to instability, i.e. due to the finite-length impulse responses, the poles of the transfer function H(z) are guaranteed to be at 0 within the unit circle in the complex plane. Hence, stability of the filter is guaranteed. Stability is not always guaranteed in IIR filters, and this was most clearly noted when several filtered output values 'blew up'.

The figure below illustrates the magnitude and phase responses of Finite Impulse Response filters:

Note the linear phase response in the lower plot.

Actual Implementation

Initially, we designed and implemented (in software) a 2-pole Infinite Impulse Response bandpass filter (with a critical frequency at 400 Hz). As described in the 'Results' section, we observed a very flat pass-band and large transition region, i.e. the roll-off was not sharp enough. We designed this filter using the equations stated in the above section entitled 'Infinite Impulse Response Filters'. To further support our design, we tried constructing a 2-pole Butterworth bandpass filter from MATLAB

We noticed further that Butterworth filters are characterized by a magnitude response that is maximally flat in the passband and monotonic overall.
Butterworth filters sacrifice rolloff steepness for monotonicity in the pass- and stopbands. Unless the smoothness of the Butterworth filter is needed, an elliptic or Chebyshev filter can generally provide steeper rolloff characteristics with a lower filter order.

Furthermore, due to the feedback loop present in implementing IIR filters, we decided that Finite Impulse Response filters would better suit our purposes. This belief was strengthened by the idea that FIR filters are not succeptible to instability.

After making the signal processing system to non-realtime, we decided to construct a 100-length FIR filter. This was done with aid of MATLAB. We noticed that MATLAB designs an FIR filter using the window method. The window method begins with an ideal lowpass filter, whose impulse response is of infinite duration, and truncates it, producing a finite impulse response.