The initial phase of our design which was the design and implementation of a single Infinite Impulse Response (IIR) filter yielded results which can be best summarized by the following plots:
The figure above describes a 2nd-order Butterworth filter with critical frequency of 400Hz. This constituted the initial phase of our spectrum analyzer design. Note the extreme flatness and attenuation of the magnitude of the frequency response. This corresponded with our observations, in that we had to reduce threshold levels significantly before even observing any output. In addition, the amplitudes of the filtered outputs were very low, specifically, less than 0.3V. Also, we believe the non-linearity present in the phase response contributed to the overall distortion of the filtered output, yielding no definite transition boundaries. In short, we could not get clean filtered output at 400Hz.
Due to the above, we decided to switch emphasis to Finite Impulse Response (see 'Filter Concepts') filters.
In comparison to the above 2-pole IIR filter (Butterworth), we present a 2-pole FIR filter. Notice the sharper roll-off, less attenuation and linear phase. These three factors, amplified by increasing the order of the filter (in our case, 100), contributed to our decision to use FIR filters:
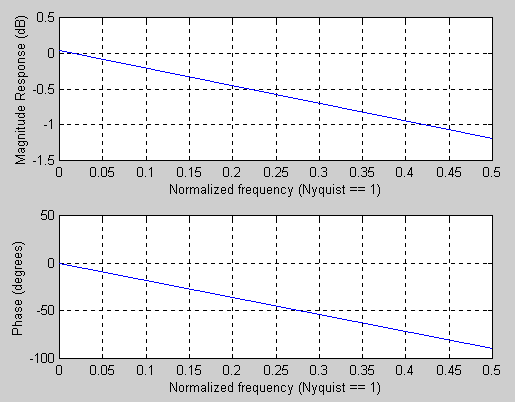
In addition, we observed the frequency response of a 100th-order FIR filter. This is shown below:
We noticed an actual 'bump' at around 400Hz (0.09
in the above magnitude plot) and linear phase around the very same region.
Hence, we implemented bandpass filters at 200Hz, 600Hz, 800Hz, 1000Hz,
1200Hz, 1400Hz and 1600Hz in addition. This essentially constituted our
spectrum analyzer.
Note the overlapping of the various bandpass filters (denoted by the different colored lines). This overlapping was the result of a non-log spacing between adjacent filter critical frequencies. As we see in the theoretical plot described in Filter Transfer Functions the measured data matched predicted responses rather well. The theoretical plot describes the overlapping between different passbands. Hence, as we sweep through intermediate frequencies, the spectrum analyzer does not register a strong affirmation for the presence of that frequency in the original signal.
Next, we also tested the analyzer with a square wave input and obtained the following Square Waves result. Square waves contain odd harmonics in its Fourier Series expansion. Apart from the initial frequencies, we observed a decrease in amplitude of higher harmonic frequencies present in the input square wave as we performed a sweep. A telling example would be the response of the analyzer to a square wave with a fundamental frequency of 200Hz. In this case, three upper harmonics were visible, and all three displayed monotonic decreasing amplitudes.
Finally, we also performed a same frequency sweep but using a triangle wave as an input. The results are here: Triangle Waves