• As described in the hardware section, Analog Devices' ADXL202 accelerometers were wired to output voltage instead of duty cycle modulated signals. This means that some A/D conversion is required for the MCU to gather information from the accelerometer. This requirement forced us to use the STK200 evaluation board and the ATmega163 MCU, since the STK500 board does not have A/D capabilities.
• We fed the output of one of the accelerometers into channel 0 of the Analog port (ADC0), and the other into channel 1 (ADC1). By alternately defining the input pin using the ADMUX control register (0b11100000 and 0b11100001), and setting the A/D converter rate using ADCSR (0x8E), we were able to sample each channel subsequently using the [ADC_INT] interrupt.
• Once we got the 8-bit word from register ADCH, we converted it to a voltage value relative to the internal analog reference voltage on the board (Aref). This voltage is unique for each board, though it is approximately 2.4 V. The simple conversion is done using the following:

  voltage = (8-bit word [dec]/256)*Aref [V]

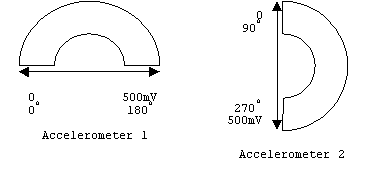
• We wanted to convert this voltage, which varies by approximately 500mV (depending on tilt angle), into units of degree. As described in the hardware section, the raw output voltage of the accelerometer was stepped down using resistors.  The voltage range we input to the A/D converter is approximately between 1.7 and 2.2V.  We subtracted the DC offset of about 1.7V from the voltage value in the program.
• The result should range between 0 and 500mV approximately. Due to the orientation of the two accelerometers, we determine whether the tilt angle is above or below 180 degrees by checking to see whether the resultant voltage from the second accelerometer is above or below 250mV.

  

  (Note: This is the basic logic we used to determine the tilt angle range, in our code we skewed the test condition slightly just so it wouldn't accidentally toggle between 0 and 180 degrees.)
• If tilt angle is between 0 and 180 degrees, we do the following:

tilt angle = (zero-offset voltage/0.5 [V])*180 [deg]

• If tilt angle is between 180 and 360 degrees, we do the following:

tilt angle = 360 [deg] - (zero-offset voltage/0.5 [V])*180 [deg]

• Due to the fluctuation in the voltage value, we chose to map it into steps of 30 degrees, by dividing and rounding off the remainder:

tilt angle = round(tilt angle/30)*30

Note: the <math.h> library we used did not have a rounding function, so instead we used the floor() and ceil() functions by testing whether the normalized remainder is greater than 0.5.

• The function used for determining the coordinates of sand (C_cal()) basically takes in the area of the sand, the tilt angle of the accelerometer, and spits out the appropriate (x,y) coordinates for the function FillQuad(). FillQuad should then draw the appropriate shape (rectangle or trapezoid) on the LCD screen.
• Due to the complexity involved, this function only works if the sand is bounded by a rectangular box. We considered other shapes more fitting to an hourglass. However, all the possible shapes that various amounts of sand can undertake complicate both C_cal() and FillQuad() drastically. Hence, the simple rectangular box was chosen for implementation.
• C_cal() first checks whether the tilt angle is 0, 90, 180, or 270 degrees. At those tilt angles the sand should bear shape of a rectangle. Upon detection it calculates the coordinates by assuming that the sand is bounded to the appropriate side of the box (2 out of 4 coordinates). It then gets the other two coordinates by dividing the the area of the sand with the length of the side.
  
  Sand shape at tilt angles 0, 90, 180 and 270 degrees

• If the tilt angle is none of the above, C_cal() then checks to see which corner the sand is bounded to (e.g. If the tilt angle is between 0 and 90 degrees, the sand should be bounded by the bottom right corner). The function then checks to see whether the shape should be a triangle or trapezoid. It does so by first assuming the shape is a triangle, and determining its base and height using Area = 1/2*base*height and tan(tilt_angle) = height/base. The function then subsequently checks to see whether the base or the height are longer than the appropriate sides of the box. (Note: We avoided cases when BOTH the base and the height are greater than their respective sides by limiting the total amount of sand possible in the hourglass. If we did not do that we would then have to deal with drawing pentagons.)
• If the sand bears a triangular shape, then C_cal() outputs coordinates of a trapezoid that closely resembles a triangle by attaching a one-pixel wide rectangle/line to the triangle. This way, function FillQuad would still be drawing a trapezoid, and it would not have to deal with multiple identical coordinates.
  
  Representation of triangle in program

• If either the base or the height of the assumed triangle is greater than its respective side of the box, C_cal() then outputs coordinates for a trapezoid that is a concatenation of a triangle and rectangle. It assumes that the longer side of the triangle (base or height) is exactly the length of the correct box side. Using that and the tilt angle, the function computes the area of the triangle, and subtracts it from the sand area. The remainder is then used to compute the width and length of the rectangle.
  
  Sand taking up shape of trapezoid

• Since we can only write a byte at a time to the LCD, drawing one pixel is not a simple task. In order to draw one pixel, we need to know which byte and which bit position to fill in so that we can write the whole byte to the LCD. The LCD is a 256 by 128 display and the starting address for graphics on the display is 0x03e8. We used the following steps to draw a pixel on the LCD:

   

  1. Find the byte position, 10 is in byte 1 (10/8)
  2. Find the bit position, 10 is in bit 2 (10 mod 8)
  3. Find what is to be written, 00100000 (because in bit 2)
  4. Find the address to write the byte by adding the graphics starting address to the byte position and then adding 40 times the line number (40 times 60 in this example). There are 40 bytes across in the LCD (although can see 32).
  5. The byte is then written to that address on the LCD.

• Function FillRect() is called to fill in a rectangle (or a square). It takes in four points and draws the rectangle that is bounded by the four points.
  
  Rectangle coordinate representation in program

• The byte and bit position of x1 and x2 are first calculated so as to know which bit and byte position to start filling in and to end filling. For example, if the rectangle to be filled in is
  
  Example of rectangle on LCD
  The starting byte position is 0 and the starting bit position is 7 (7 mod 8). The ending byte position is 4 and the ending bit position is 1 (33 mod 8). (Bit positions and byte positions start from 0)
• Based on bit positions at the extreme ends, we are able to first fill in the bytes at the ends. Using the above example, the starting byte would be filled in as 0000001 (bit 7 is the only one filled in). The ending byte would be filled in as 11000000 (the last bit filled in is bit 1).
• The next thing is to fill in what is between the starting byte and the ending byte. These are all filled in as 11111111 since we want all the pixels to be filled in.
• Each line is filled in the same way (from line 6 to line 50 in the example above) to completely fill in the rectangle.

• Function FillQuad() is called to fill in a quadrilateral. It takes four points and fills in the quadrilateral. Any quadrilateral with one slanted line is considered a trapezoid. Since we limited the sand to bear shapes of either a rectangle or trapezoid, this function detects at most one slanted line.
• All trapezoids can be made into rectangles:

  

  Imaginary rectangle bounding trapezoid

  The function first determines whether one of the sides of the quad is a slanted line or not by calling Slant(). If there are no slanted lines, then the shape is a rectangle and FillRect() is called; a rectangle is drawn and filled on the LCD. If there is a slanted line, then the program gets more complicated.
• Slant() records which side of the quadrilateral is slanted. It also keeps track of a temporary position, which will allow one of the endpoints to be replaced so that a rectangle can be made from the trapezoid (see above figure). FillRect() is then called, filling the rectangle made by the temporary position.
• Our next step is to "unfill" the points that are not really part of the quadrilateral. To do so, we use Slope() to get the slope and the y-intercept of the slanted line. These two values allow us to get the equation of the slanted line.
• In CheckandUnfill(), we then subject all the points within the temporary rectangle to the equation of the slanted line. Using Matlab, we determined the cases when a pixel would be unfilled. Depending on which side of the quadrilateral is slanted and whether its slope is positive or negative, the unfill region could be greater than or less than the value obtained from y = mx+b.
• If the point needs to be "unfilled", we call UnfillPoint(). Unfilling a point uses almost the same methodology as the FillRect(). Basically, the bit and the byte of the point are determined. The first time a byte is entered, we assume the byte is 0xFF (BYTE). This is a logical assumption since the rectangle should be initially filled from the FillRect(). The only exception to this is if the byte is at the beginning or the end of the rectangle (which we explain later in this section).
• Depending on the bit of the current byte that the point being checked is at, a different byte is ANDed to BYTE. For example, if the position is at the first bit, then BYTE is ANDed with 0b01111111 (first bit is 0), if the position is at the second bit, then BYTE is ANDED with 0b10111111 (second bit is 0), etc.
• Now we can take care of the exception previously mentioned involving a byte at the beginning or the end of the rectangle. When the first point (of the row) in a rectangle is in the middle of a byte, BYTE must be ANDed with something so that pixels outside of the rectangle are not filled. The "something" that BYTE is ANDed with is dependent on the bit. If the bit is in the middle of the byte, then every bit before this bit must be zeroed out. The same logic follows if the last point (of the row) of the rectangle is in the middle of a byte. BYTE must be ANDed with something so that every bit after this bit is zeroed out.
• Another check that we had to put into the code was if the y position of the point equals mx+b and the point was the first or last point of the slanted line. If this is true, instead of calling UnFillPoint(), UnfillRest() is called. When a point falls under the previously mentioned condition, it will cause a skip in a bit and write the wrong value to the LCD. We take care of it through ANDing BYTE with slightly different values than UnFillPoint().
• All of these checks and precautions are placed in the code due to the writing scheme for the LCD, which writes only bytes, not bits.

• The alarm was implemented by using the [TIM1_COMPA] (compare on match) interrupt in timer1. Although we did not require the accuracy that timer1 provides, we used it because of the ease. We just had to set OCR1A to the frequency and turn on timer1 through TCCR1B control register.
• The alarm is turned on each time the sand finishes falling from one side of the hourglass to the other. It is only turned off when the user pushes button 0 and tilts the hourglass a little to get it out of the "falling sand" mode.