An active noise canceler to eliminate the 60 Hz noise found in electrical signals due to AC power-line contamination.
60 Hz noise is frustrating for anyone trying to make sensitive measurements of low voltage processes (eg. Electrocardiogram measurements), record audio from electrical instruments (eg. guitar "hum"), or use electronic systems near an AC transformer. The most common way to eliminate the noise is through a 60 Hz notch filter. Because there are inherent variations in the 60 Hz signal, a notch filter is not robust against signal source frequency changes. However, using a microcontroller such as the ATMega32 to monitor a reference signal and output an out-of-phase signal to cancel the noise, we overcome the limitations of a single-frequency selective notch filter and can achieve at least 15 dB cancellation of 60 Hz component in the contaminated signal. Digital Signal Processors (DSPs) or Field Programmable Gate Arrays (FPGAs) can be programmed for this purpose, but are substantially more expensive than the ATMega32.
This project was undertaken during a five-week design lab for ECE 476 with Professor Bruce Land (TA: Adrian Wong) at Cornell University.
Robert Ochshorn (rmo25)
Kyle Wesson (kdw24)
Design
Rationale and Source of Project Idea
The original goal of our project was to adaptively cancel sound noise in a rapidly changing environment such as the interior of a vehicle. We were able to find numerous reference papers that had accomplished similar goals. While we have not given up hope that we can cancel audible noise, several factors (eg. poorly functioning microphones, processor speed) have prevented us from achieving this specific goal to date. However, adaptively cancelling audio is a very similar problem to canceling electrical noise.
Early in the semester, our Professor, Bruce Land, suggested making an adaptive noise canceler to help neurobiology researchers who need to make sensitive, noiseless measurements. He had completed some preliminary simulations of adaptive cancellation in Matlab and created a block diagram of a potential solution. We decided to work on this since it would be an excellent first step to the ultimate goal of (sound) noise cancellation.
Background Math
From the start, we settled on a least mean squares (LMS) adaptive filter design. A LMS filtering approach is well known and well documented (see references). The goal is to continually update a set of weights that change the output of the system. This output (also known as the error signal) is fed back into the filter which modifies its weights according to the ultimate desired signal.
The best description of the LMS filtering algorithm was found in Active Noise Control Systems: Algorithms and DSP Implementations (Sen M. Kuo and Dennis R. Morgan, Wile & Sons, 1996) which we excerpt here:
-
Choose parameters and initial conditions: l,
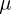 , and
w[0], where l is the order of the filter,
, and
w[0], where l is the order of the filter, 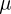 is the
step size, and w[0] is the initial weight vector at time n = 0.
is the
step size, and w[0] is the initial weight vector at time n = 0.
-
Compute adaptive filter output:
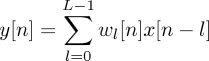
- Compute the error signal: e[n] = d[n] - y[n].
- Update adaptive weight vector from w[n] to w[n+1] using the LMS algorithm:

The math to determine our filter characteristics is documented in the implementation section. In order to eliminate any possible aliasing, we need to sample at a rate consistent with the Nyquist theorem. Since we decided to cancel below about 230 Hz signals, our input sampling frequency needs to be at least 460 Hz, and we need to lowpass the contaminated signal.
Logical Structure
In one sentence: our project takes in a contaminated signal, a reference signal, and outputs a "anti-noise" signal that is summed with the contaminated signal to produce a clean "final" signal.
Control Flow
Our software is structured into three primary components:
- an output interrupt on timer0 that writes to PWM at full clock speed with an interrupt on counter overflow:
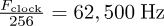
- an input interrupt on timer2 that muxes analog in between the
reference and error source, performs the a/d conversion, and sets
program state to flag a new value as ready; this runs with a
clk/64 prescaler:
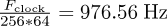
- finally, the main loop polls state set in the input interrupt and either updates filter weights based on a new error signal, or computes output based on a new input.
Hardware and Software Tradeoffs
We needed to make both hardware and software tradeoffs in our design. Since the ATmega32 only runs at 16 MHz, we needed to be realistic about the frequency range we could cancel. The larger frequencies will require more clock cycles to get the input reference signal. In addition, larger filter lengths require more multiply and accumulate (MAC) operations. Thus, we have a tradeoff between the quality of our adaptive filter and the amount of time we have to process and generate the anti-signal. We decided that it was reasonable given the constraints of the system to adaptively cancel frequencies below 230 Hz.
We also made some hardware tradeoffs. We originally intended to use a four-pole lowpass Butterworth filter with cutoff frequency of 250 Hz to filter the pulse width modulated output from the ATmega32 into the output waveform. However, we learned that the Butterworth filter, while having the flattest frequency response, has an inherent phase delay. Because our filter needs to output the correct signal within a small tolerance relative to the reference signal, using the higher-quality filter was not practical. Instead, we used a simple RC filter with a cutoff frequency of about 200 Hz (the RC filter doesn't have a steep cutoff).
A persistent source of frustration was the ATmega32's A/D converter input voltage range. Because we choose to use a 2.56 internal reference voltage, our range was limited to 0 - 2.56 V. While the range is reasonable (since the input and output signals could be 1 V peak-to-peak), the range forces us to DC bias the input signal to roughly 1.25 V for a full "range" in the ADC. Since none of the signals we used were biased to 1.25 V, we needed to constantly consider the peak-to-peak and mean voltage of our input signals and rebias them accordingly. If the ATmega32's ADC could have dealt with a plus/minus voltage or if we used an external ADC that automatically rebiased the range, we might have had an easier time dealing with a various assortment of input signals (ie. mics, guitars).
Standards, Patents, Copyrights
There is one standard that is the reason for our project: 60 Hz power line transmission. Because the U.S. power grid transmits power at 60 Hz, this frequency is public (noise source) enemy number one. Thankfully, we are also able to take advantage of this to cancel the noise using an AC transformer to obtain a reference signal.
There are also standards we are using inherently that we have not paid much attention to such as the standard we are using to "program" the ATmega32, the USB to serial connection from the computer to the STK500 board, the standardization of batteries (9V), and the standard operational amplifier "golden rules."
Certainly cancelling 60 Hz noise is not a new topic and there are certainly patented removal techniques, patents on notch filters, and studies of noise cancellation. However, we are unaware of any adaptive noise cancelers that use a low-cost microcontroller such as the ATmega32. One device we came across is the Hum Bug Noise Eliminator. However, we were unable to find out any more information regarding the product such as price, speed, power supply, etc.
Implementation
The final hardware selection ended up being a small subsection of all the hardware we built. The additional hardware section has links to all circuit schematics we made and gives reasons we did not use them.
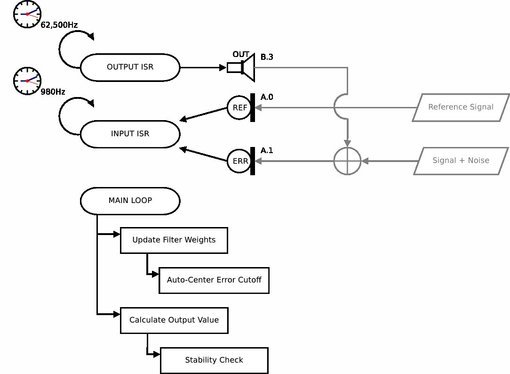
The hardware we did use is detailed here. It included two operational amplifier adder stages (to generate the noise and clean signal), an AC transformer stage (to get a reference signal), and a simple RC filter (to convert the pulse width modulated signal to a sinusoidal signal).
Final Hardware Implementation
60 Noise Cancellation System: Block Diagram
This is the overall noise cancellation technique we use. Here we show the entire system in a reduced "block diagram" format. Input/output pins are shown on the ATmega32.
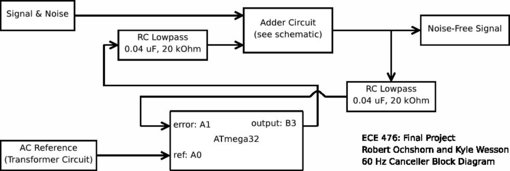
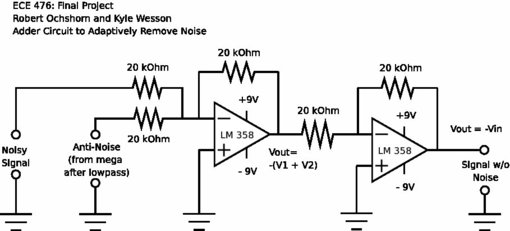
Noise Adder (60 Hz Adaptive Noise Cancellation)
This circuit is used to create a 60 Hz contaminated signal for adaptive filter cancellation. Since we need to be able to test our adaptive algorithm with a well-known and understood signal, we used this non-inverting adding circuit so that we can sum a 60 Hz "noise" signal and a valid reference signal. We use one function generator to make a "clean" signal and sum it with the output of the transformer circuit shown below.
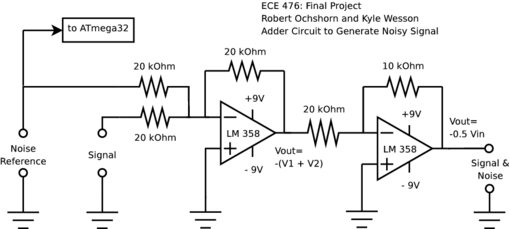
Noise Remover (60 Hz Adaptive Noise Cancellation)
This circuit takes in the noise contaminated signal and an adaptive output signal from the ATmega32 and sums them to remove the contamination. The overall output is then fed back to the ATmega32 as an error reference signal through a RC lowpass to prevent aliasing.
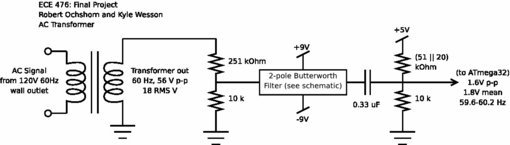
AC Transformer Input Converter
We used an AC transformer to adaptively cancel "real" 60 Hz noise in from the 120 V powerlines (the standard voltage and frequency of powerlines across the U.S.). In order to obtain an reference voltage suitable for the ATmega32, we used the following circuit. The AC transformer takes in a 56 V peak-to-peak signal (18 V RMS) and converts it to a 1.6 V peak-to-peak, 1.8 V DC offset. We are using a 2.56 V reference voltage on the ATmega32 ADC.
RC Filter
The RC lowpass to filter the PWM out from the ATmega32 was made of a 20k Ohm resistor and a 0.04 uF capacitor so that it has a cutoff frequency of about 230 Hz. Because are resistors and capacitors are only valid to 5% and because the RC doesn't have the steepest cutoff, the cutoff frequency is appropriate for the function.
Final Software Implementation
Generating the Antinoise
We implemented a microcontroller-based, fixed-point adaptive Finite Impulse Response (FIR) filter, so we compute output by summing the product of weights and previous inputs:
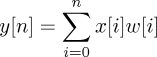
To avoid an undesired high-frequency harmonic, we output our signal pulse width modulated at the maximum rate supported by the ATMega32: 62,500 Hz. We do this through an interrupt, which linearly interpolates between desired outputs, determined every 128 outputs. Since the sample rate and the output rate are related by a power of two, we can find an appropriate increment for the interpolation with a simple right shift.
Further, we can check for instability by comparing an output with the previous output. If the difference is too great, we revert to an older version of the weights and try again, resetting completely to blank weights if that did not work.
Filter Characteristics
Since we are targeting 60 Hz noise, we can optimize our filter for that purpose. We have a filter length of eight, at a sample rate for the input of 488 Hz, which gives us an ideal window size of 61 Hz:
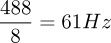
This means that each sample is 45 degrees apart in the 60 Hz reference signal, producing ideal conditions for adapting.
Adapting Weights
We are using a heavily-optimized LMS algorithm where weights are updated such that
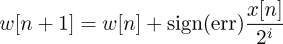
where i is an amalgamation of mu and the magnitude of the error, precomputed for use as a right-shift each time we update the weights. This is extremely computationally efficient, requiring only an addition and a right shift for each weight, but still giving us substantially faster convergence than a signed LMS that does not take error magnitude into account.
Fixed-point Math
Floating point arithmetic is not practical with the computational limitations of the ATMega32 and the speed required. We used a 16:16 fixed-point system based on Prof. Land's fixed point page. Using GCC, we found that simple C defines would produce code optimized far better than we could imagine writing by hand in assembly. All of our inputs were coming in from the internal A/D, so we never actually needed to multiply two fixed-point numbers; we defined a multiplication between a fixed-point number and a character:
#define multFix80(a,b) (((a*((signed long)b))))(Additional) Hardware
We went through a lot of hardware that we ended up not needing for various reasons (the largest of which was that our project changed a little over halfway through the design period).
The first hardware component we ended up not using was the microphones we purchased which we found almost useless in detecting sound and very finicky to use (they required a large capacitor which seemed to affect the rest of our circuits in a negative way). We spent at least five hours simply working with the mics to debug their very simple wiring and were never impressed with their functionality.
We also didn't need the two four-pole lowpass Butterworth filters which were going to be used for low-pass filtering the microphone inputs (although we did use a two-pole Butterworth filter as described above).
Since we didn't need to make sound, we didn't need the bass boost amplifier we made with the LM386 operational amplifier. It sounds sweet though and had 46 dB gain to get your funk on with just one 9 V battery!
Results
We believe we have created a project which cancels 60 Hz noise very well given the hardware and software limitations of a ATmega32 microcontroller running at 16 MHz.
In a typical test:
- Function Generator "Signal": 220 Hz, 250 mV peak-to-peak
- AC Line "Reference": 60 Hz, 672 mV peak-to-peak
- Signal to Noise Ratio: 0.27
We were able to obtain the following results:
- Total signal output (center to average peak): 60 mV
- Noise peak average: 12 mV
- Recovery Rate: 83%
- Output frequency accurate to within 3% of the desired signal
Furthermore, the convergence time of the noise canceller is within seven seconds. There is minimal error in the output signal we generate because we interpolated between the output points. Our system can also determine if it looses stability and resets. Because of the quick convergence time, this is almost unnoticeable.
We tried to be as safe as possible in our final design. We only used one reference from the 120 V AC line and this was through an 18 V (RMS) transformer. We also used 9 V batteries for the rest of our circuitry so that electrical shock was as minimal as it could be given the context of a working electrical circuit.
Video
(no flash player installed)(no flash player installed)(no flash player installed)Conclusions
The results we achieved were satisfying although we both plan to spend some additional time working with audio (generating anti-sound and working with guitar hum). Had we started immediately with 60 Hz noise cancellation, we might have been able to finish the project with a little more time remaining to then try the audio, rather than the other way around. But then again, it's a philosophical question: does the path choose the walker or the walker choose the path?
One thing that we would like to do is to make the input and output signals more robust in terms of their accepted values and biasing. It would be great to make a generalized noise cancellation box that could take in any plus/minus voltage within a range, rescale and rebias it, and output the cleaned signal without the reference noise. Another possible improvement would be to port the design to a printed circuit board to eliminate a lot of the variations and settle on a final design. This could be tested by researchers here at Cornell in the neurobiology department and the results could lead to a paper. This work could also lead to a patent if we choose to pursue it.
As far as we know, there are no applicable standards for our design to follow. We are generating "destructive" interference, but this is for a constructive purpose. It should not interfere with other design any more than the 60 Hz noise from the power-lines already do.
We were very careful to properly credit our sources and list all of the background research that we used. We did not use someone else's code in our final design (although we used Professor Land's Matlab Simulations as a basis for our own).
A source of pride in our project was stepping away from CodeVision and moving to the GNU C Compiler (GCC). In addition to escaping a wretched interface, and even notwithstanding the far-superior optimizations GCC offers, we believe that using free software compilation tools was an important move so that our code can be reloaded, shared, and modified without any proprietary lock-in.
We did not reverse engineer a design, sample any parts, or sign any non-disclosure agreements. We also do not use a transmitter or have any FCC regulations to conform to. We know of no known legal issues with the project (except that it cannot be used in medical devices or for any medical purpose).
Ethics
Throughout the project, we have acted in a manner consistent with the IEEE Code of Ethics.
We have no conflicts of interest (no parts were sampled), have rejected any bribery (though none was present), have not injured anyone, and have treated all people fairly. Throughout the five weeks of the project, we have been helpful and fair to others working in the lab and respectful of their work. This was very important, especially in the last few weeks when time and lab space become limited. To our knowledge, we have not harmed anyone else's project or done damage to any laboratory equipment.
We strove to increase our technical competence and abilities to make our project better. We researched the topic, read papers and books, and tried out many techniques we had never used before to reach the final product. However, our project would not be the same without the numerous criticism and suggestions we received from many sources. We strived to give credit to all who have helped us along the way.
One of the most important ethical considerations of our project involves the impact on other people. While we accept responsibility to make technical decisions and realize that our project has great potential to help many people, we must state that our product has not met the rigorous standards required to be used in any medial devices. We have been honest in estimating the project's abilities, but cannot accept the large responsibility of making this project conform to medical standards in the short five weeks of lab.
Appendix
The code!
Weekly Update Archive
Budget
Prototype Board
QUANTITY ITEM UNIT COST TOTAL COST NOTES -- -- -- $13.80 -- 1 ATMega32 $8 $8 1 ECE 476 Prototype Board $5 $5 6 Header Socket Pins $0.05 $0.30 1 DIP Socket $0.50 $0.50 Mega32 sits in this Lowpass Filter
QUANTITY ITEM UNIT COST TOTAL COST NOTES 1 -- $3.63 $3.63 -- 2 9V Battery $0.47 $0.94 purchased from WalMart; receipt available 1 Solder Board $2.50 $2.50 cut in half to make one circuit 4 Header Pins $0.05 $0.20 easy to grab 1 LM 358 free free free in lab Adder Circuit
QUANTITY ITEM UNIT COST TOTAL COST NOTES 1 -- $3.94 $3.94 -- 2 9V Battery $0.47 $0.94 purchased from WalMart; receipt available 1 Solder Board $2.50 $2.50 cut in half to make one circuit 10 Header Pins $0.05 $0.50 easy to grab 2 LM 358 free free free in lab Additional Items
QUANTITY ITEM UNIT COST TOTAL COST NOTES -- -- -- $11.00 -- 1 AC transformer free free free from Bruce 1 Protoboard $6.00 $6.00 used for demo but not needed in final design 1 Power supply $5.00 $5.00 used for demo but not needed in final design Total: $32.17 (as shown in demo, actually cheaper if made on PCB)
References
[1] Digital Signal Processing and the Microcontroller. Prentice Hall PTR, 1999. [ bib ] [2] M. O. Tookhi and R. R. Leitch. Active Noise Control. Oxford Engineering Science Series - 29. Clarendon Press, 1992. [ bib ] [3] Sen M. Kuo and Dennis R. Morgan. Active Noise Control Systems: Algorithms and DSP Implementations. Wiley Series in Telecommunications and Signal Processing. Wiley & Sons, 1996. [ bib ] [4] Simon Haykin and Bernard Widrow. Least-Mean-Square Adaptive Filters. Wiley Series in Adaptive and Learning Systems for Signal Processing. Wiley & Sons, 2003. [ bib ] [5] Richard Haddad and Thomas Parsons. Digital Signal Processing: Theory, Applications, and Hardware. Computer Science Press, 1991. [ bib ] [6] Simon Haykin. Adaptive Filter Theory. Prentice Hall Information and System Science Series. Prentice Hall, 1996. [ bib ] [7] Sen M. Kuo and Brian M. Finn. An integrated audio and active noise control system. Technical report, IEEE, 1993. [ bib ] [8] Hiroshi Uchida, Norihiko Nakao, and Tetsuro Butsuen. High performace active noise control system for engine noise in a car cabin. Technical Report 940608, SAE, 1994. [ bib ] [9] Trevor Sutton, Stephen Elliott, Malcom McDonald, and Timothy Saunders. Active control of road noise inside vehicles. Technical report, jul 1994. [ bib ] [10] IEEE Transactions on Speech and Audio Processing. Active Control System for Low-Frequency Road Noise Combined with and Audio System, volume 9, 2001. [ bib ] [11] M. de Diego, Gonzalez, G Pinero, M. Ferrer, and JJ Garcia-Bonito. Subjective evaluation of actively controlled interior car noise. Technical report, IEEE, 2001. [ bib ] [12] Gary Elko. Adaptive noise cancellation with directional microphones. Technical report, Bell Labs. [ bib ] [13] Ahmen Elhossini, Shawki Areibi, and Robert Dony. An fpga implementation of the lms adaptive filter for audio processing. Technical report, University of Guelph. [ bib ] [14] Antonio Di Stefano, Alessandro Scaglione, and Costantino Giaconia. Efficient fpga implementation of an adaptive noise canceller. Technical report, IEEE, 2005. [ bib ] [15] A. Karakasoglu, J.F. Abbott, and S.C. Douglas. A low-cost multichannel active noise control system for personal quietude. Technical report, IEEE, 1996. [ bib ] [16] Bruce Land. Digital filtering for atmel mega32. Technical report, Cornell University. [ bib ] [17] Robert Bernhard. Active control of road noise inside automobiles. Technical report, Active 95, 1995. [ bib ] [18] Rafael Ramos, Antoni Mànuel-Làzaro, Joaquín Del Rio, and Gerard Olivar. Fpga-based implementation of an adaptive canceller for 50/60-hz interference in electrcardiography. Technical report, IEEE, 2007. [ bib ] [19] Lawrence Fisher. Adding noise to cut a car's noise. 1990. [ bib ] [20] Honda. Honda accord hybrid sedan, 2004. http://honda.com. [ bib ] [21] Bruce Land. Adaptive noise cancellation, 2007. http://instruct1.cit.cornell.edu/Courses/ece576/DE2/fpgaDSP.html. [ bib ] Breakdown
For this project, Rob focused mainly on software while Kyle focused mostly on hardware. However, the majority of the project was done together in lab and at Rob's apartment.

