Boids!

ECE 4760, Fall 2021, Adams/Land

Spring, 2021 version

HTML('''<script>
code_show=true; 
function code_toggle() {
 if (code_show){
 $('div.input').hide();
 } else {
 $('div.input').show();
 }
 code_show = !code_show
} 
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()"><input type="submit" value="Click here to toggle on/off the raw code."></form>''')

import numpy
import matplotlib.pyplot as plt
from IPython.display import Audio
from IPython.display import Image
from scipy import signal
from scipy.fft import fftshift
from scipy.io import wavfile
plt.rcParams['figure.figsize'] = [12, 3]
from IPython.core.display import HTML
HTML("""
<style>
.output_png {
    display: table-cell;
    text-align: center;
    vertical-align: middle;
}
</style>
""")

Table of Contents

• Background and Introduction
• Algorithm Overview

  • Separation
  • Alignment
  • Cohesion
  • Screen edges
  • Predator avoidance (ECE 5730 only))
  • Speed limits
  • Update position
  • Recommended parameter values
  • Pseudocode

• Fixed Point Arithmetic
• Frame Rate
• Hardware connections to PIC32
• Program Organization
• Weekly Checkpoints and Lab Report Specifications

  • Week one
  • Week two
  • Week three
  • Lab Report
  • Opportunities to keep going

• Demonstrations of Working System (for reference)

Background and Introduction

Boids is an artificial life program that produces startlingly realistic simulations of the flocking behavior of birds. Each "boid" (which is an abbreviation of "bird-oid object" follows a very simple set of rules. These rules will be discussed at length, but they can be summarized as follows:

• Separation: boids move away from other boids that are too close
• Alignment: boids attempt to match the velocities of their neighbors
• Cohesion: boids move toward the center of mass of their neighbors

ECE 5730 students will implement a fourth rule, which is predator avoidance. Boids will turn away from a randomly moving predator.

When all of the boids follow these simple rules, the flock produces gorgeously organic-looking emergent patterns, as shown in the video below. You can compare the behavior shown in the simulation below to videos of actual murmurations of starlings (like this one). These rules are also extendable. You might add a predator that all the boids must avoid, or you might add a "perching" behavior where boids near the bottom of the screen rest for a moment before rejoining the flock. The Boids algorithm was developed by Craig Reynolds in 1986.

In this lab, you will create a flock of boids on the TFT that will be animated at (at least) 30 fps. You are challenged to produce the largest flock that you can. The parameters which govern boid behavior will be programmable via a Python user interface, and the flock will instantly begin behaving according to the updated parameters.

Algorithm Overview

Just like in nature, no boid has global knowledge of every other boid in the flock. Instead, each can only see boids that are within its visual range and that are within its smaller protected range. These are tunable parameters. A boid will move away from other boids that are within its protected range (birds don't want to fly into each other), it will attempt to match the average velocity of boids within its visible range, and it will tend toward the center of mass of boids in its visible range.

We will also enforce minimum and maximum speed limits for the boids. Flocking birds (like starlings) are never stationary in flight. So, we'll prevent the speed of any boid from dropping below some tunable value. Birds also have maximum speeeds, so we'll prevent the speed of any boid from exceeding some tunable value. Finally, we want for the boids to turn around when they reach the edges of the TFT screen. When a boid gets within some tunable margin of an edge of the screen, we will turn it by some tunable value. The greater this value, the faster the birds will be able to turn. We can play with these parameters until we get realistic-looking behavior.

The state for each boid includes its x/y position and its x/y velocity, represented as:
boid.x
boid.y
boid.vx
boid.vy

Each boid determines whether each other boid is in its protected/visual range.

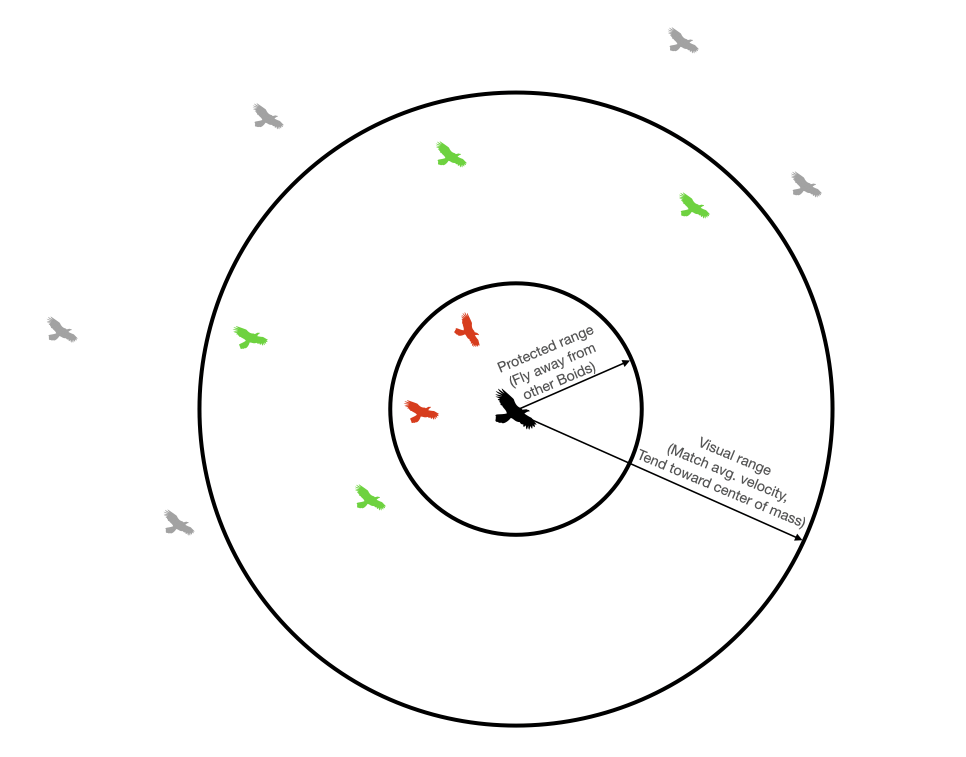
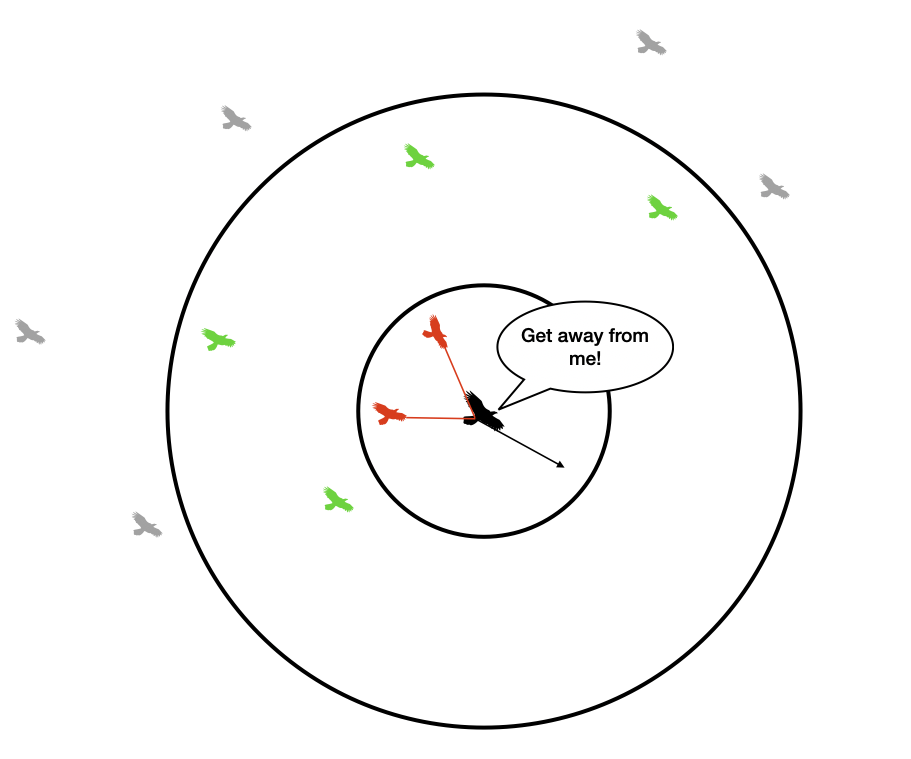
Separation

Each boid attempts to avoid running into other boids. If two or more boids get too close to one another (i.e. within one another's protected range), they will steer away from one another. They will do so in the following way:

1. At the start of the update for a particular boid, two accumulating variable (close_dx and close_dy) are zeroed
2. We loop thru every other boid. If the distance to a particular boid is less than the protected range, then
   close_dx += boid.x - otherboid.x
close_dy += boid.y - otherboid.y.
3. Once we've looped through all other boids, then we update the velocity according to
   boid.vx += close_dx*avoidfactor
boid.vy += close_dy*avoidfactor
   (where avoidfactor is a tunable parameter)

Move away from boids in protected range.

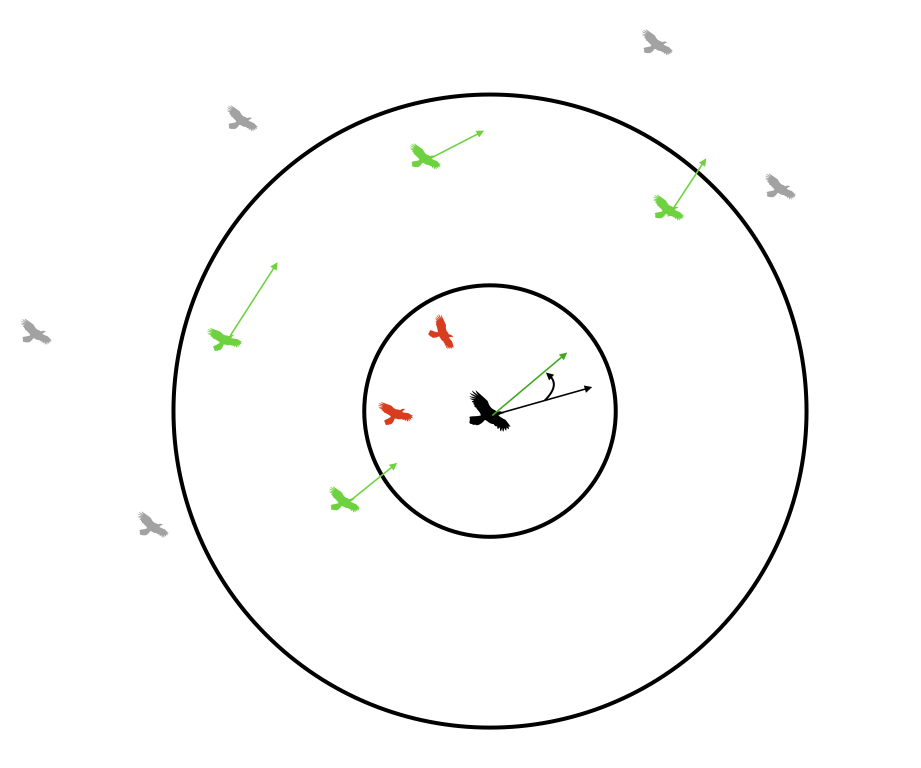
Alignment

Each boid attempts to match the velocity of other boids inside its visible range. It does so in the following way:

1. At the start of the update for a particular boid, three variables (xvel_avg, yvel_avg, and neighboring_boids) are zeroed
2. We loop thru every other boid. If the distance to a particular boid is less than the visible range, then
   xvel_avg += otherboid.vx
yvel_avg += otherboid.vy
neighboring_boids += 1
3. Once we've looped through all other boids, we do the following if neighboring_boids>0:
   xvel_avg = xvel_avg/neighboring_boids
yvel_avg = yvel_avg/neighboring_boids
4. We then update the velocity according to:
   boid.vx += (xvel_avg - boid.vx)*matchingfactor
boid.vy += (yvel_avg - boid.vy)*matchingfactor
   (where matchingfactor is a tunable parameter)

Align with average velocity of boids in visible range.

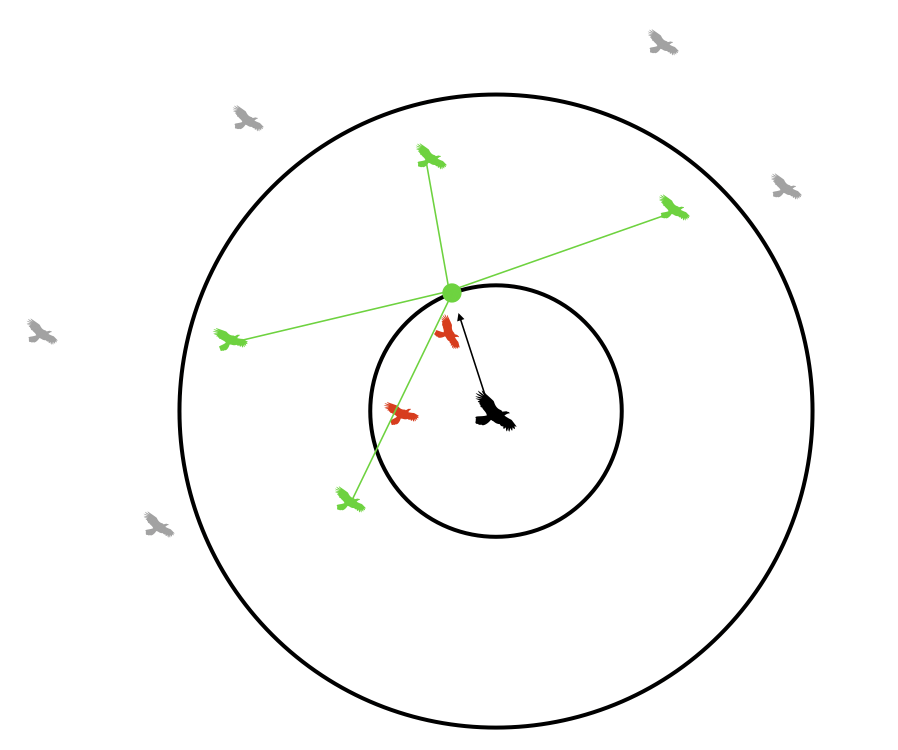
Cohesion

Each boid steers gently toward the center of mass of other boids within its visible range. It does so in the following way:

1. At the start of the update for a particular boid, three variables (xpos_avg, ypos_avg, and neighboring_boids) are zeroed
2. We loop thru every other boid. If the distance to a particular boid is less than the visible range, then
   xpos_avg += otherboid.x
ypos_avg += otherboid.y
neighboring_boids += 1
3. Once we've looped through all other boids, we do the following if neighboring_boids>0:
   xpos_avg = xpos_avg/neighboring_boids
ypos_avg = ypos_avg/neighboring_boids
4. We then update the velocity according to:
   boid.vx += (xpos_avg - boid.x)*centeringfactor
boid.vy += (ypos_avg - boid.y)*centeringfactor
   (where centeringfactor is a tunable parameter)

Move toward center of mass of boids in visible range.

Screen edges

We want our boids to turn-around at an organic-looking turn radius when they approach an edge of the TFT. We will do so in the following way:

if boid.x < leftmargin:
    boid.vx = boid.vx + turnfactor
if boid.x > rightmargin:
    boid.vx = boid.vx - turnfactor
if boid.y > bottommargin:
    boid.vy = boid.vy - turnfactor
if boid.y < topmargin:
    boid.vy = boid.vy + turnfactor

where turnfactor and all margins are tunable parameters. I recommend a margin of 50 pixels on all edges.

Steer away from edges of TFT display.

Predator avoidance (ECE 5730 only)

ECE 5730 students are required to add at least one predator to the simulation. This predator moves like any other Boid, except that its only velocity updates come from turning at the screen edges (it does not perform any separation, cohesion, or alignment calculations).

The Boids, of course, avoid the predator. They do so in the following way:

1. For each Boid compute the distance from the Boid to the predator in each dimension:
   predator_dx = boid.x - predator.x
predator_dy = boid.y - predator.y
   
2. If the distance to the predator is less than the predatory range (a tunable parameter), then turn away from the predator:
   

   if (predator_dy > 0) { //predator above boid
   boid.vy = (boid.vy + predatorturnfactor) ;
   }
   if (predator_dy < 0) { //predator below boid
   boid.vy = (boid.vy - predatorturnfactor) ;
   }
   if (predator_dx > 0) { //predator left of boid
   boid.vx = (boid.vx + predatorturnfactor) ;
   }
   if (predator_dx < 0) { //predator right of boid
   boid.vx = (boid.vx - predatorturnfactor) ;
   }
   

   where predatorturnfactor, similarly to turnfactor, dictates how sharply a boid is capable of turning away from a predator.

Speed limits

We constrain the boids to move faster than some minimum speed and slower than some maximum speed. We do so in the following way:

1. Once the velocity has been updated, compute the boid speed
   speed = sqrt(boid.vx*boid.vx + boid.vy*boid.vy)
2. If speed>maxspeed:
   boid.vx = (boid.vx/speed)*maxspeed
boid.vy = (boid.vy/speed)*minspeed
3. If speed<minspeed:
   boid.vx = (boid.vx/speed)*minspeed
boid.vy = (boid.vy/speed)*minspeed

Update position

With the updated velocity, we update the boid position. Assume that $\Delta t = 1$ from frame to frame (i.e. that velocity is in units of pixels/frame):

boid.x = boid.x + boid.vx
boid.y = boid.y + boid.vy

Recommended parameter values

You can play with these to get different emergent behaviors. These are the parameters that I used in the example videos on this webpage. Note that you will need to convert these to fixed-point. I recommend using the type _Accum for all arithmetic.

turnfactor: 0.2
visualRange: 20
protectedRange: 2
centeringfactor: 0.0005
avoidfactor: 0.05
matchingfactor: 0.05
maxspeed: 3
minspeed: 2

ECE 5730 students

predatorturnfactor: 0.4
predatorRange: 50

Pseudocode

All of the above rules are represented in the below pseudocode.

# For every boid . . .
for each boid (boid):

    # Zero all accumulator variables
    xpos_avg, ypos_avg, xvel_avg, yvel_avg, neighboring_boids, close_dx, close_dy = 0

    # ECE 5730 students only, also zero accumulator variables associated with predator
    num_predators, predator_dx, predator_dy = 0

    # For every other boid in the flock . . .
    for each other boid (otherboid):

        # Compute differences in x and y coordinates
        dx = boid.x - otherboid.x
        dy = boid.y - otherboid.y

        # Are both those differences less than the visual range?
        if (abs(dx)<visual_range and abs(dy)<visual_range):  

            # If so, calculate the squared distance
            squared_distance = dx*dx + dy*dy

            # Is squared distance less than the protected range?
            if (squared_distance < protected_range_squared):

                # If so, calculate difference in x/y-coordinates to nearfield boid
                close_dx += boid.x - otherboid.x 
                close_dy += boid.y - otherboid.y

            # If not in protected range, is the boid in the visual range?
            else if (squared_distance < visual_range_squared):

                # Add other boid's x/y-coord and x/y vel to accumulator variables
                xpos_avg += otherboid.x 
                ypos_avg += otherboid.y 
                xvel_avg += otherboid.vx
                yvel_avg += otherboid.vy

                # Increment number of boids within visual range
                neighboring_boids += 1 

    ####################################################################################
    ######################### 5730 students only #######################################
    ####################################################################################
    # For every predator . . .
    for each predator (predator):

        # Compute the differences in x and y coordinates
        dx = boid.x - predator.x
        dy = boid.y - predator.y

        # Are both those differences less than the predatory range?
        if (abs(dx)<predatory_range and abs(dy)<predatory_range):

            # If so, calculate the squared distance to the predator
            squared_predator_distance = dx*dx + dy*dy

            # Is the squared distance less than the predatory range squared?
            if (squared_predator_distance < predatory_range_squared):

                # If so, accumulate the differences in x/y coordinates to the predator
                predator_dx += boid.x - predator.x
                predator_dy += boid.y - predator.y

                # Increment the number of predators in the boid's predatory range
                num_predators += 1

    # If there were any predators in the predatory range, turn away!
    if (num_predators > 0):
        if predator_dy > 0:
            boid.vy = boid.vy + predator_turnfactor
        if predator_dy < 0:
            boid.vy = boid.vy - predator_turnfactor
        if predator_dx > 0:
            boid.vx = boid.vx + predator_turnfactor
        if predator_dx < 0:
            boid.vx = boid.vx - predator_turnfactor     
    ####################################################################################

    # If there were any boids in the visual range . . .            
    if (neighboring_boids > 0): 

        # Divide accumulator variables by number of boids in visual range
        xpos_avg = xpos_avg/neighboring_boids 
        ypos_avg = ypos_avg/neighboring_boids
        xvel_avg = xvel_avg/neighboring_boids
        yvel_avg = yvel_avg/neighboring_boids

        # Add the centering/matching contributions to velocity
        boid.vx = (boid.vx + 
                   (xpos_avg - boid.x)*centering_factor + 
                   (xvel_avg - boid.vx)*matching_factor)

        boid.vy = (boid.vy + 
                   (ypos_avg - boid.y)*centering_factor + 
                   (yvel_avg - boid.vy)*matching_factor)

    # Add the avoidance contribution to velocity
    boid.vx = boid.vx + (close_dx*avoidfactor)
    boid.vy = boid.vy + (close_dy*avoidfactor)


    # If the boid is near an edge, make it turn by turnfactor
    if outside top margin:
        boid.vy = boid.vy + turnfactor
    if outside right margin:
        boid.vx = boid.vx - turnfactor
    if outside left margin:
        boid.vx = boid.vx + turnfactor
    if outside bottom margin:
        boid.vy = boid.vy - turnfactor

    # Calculate the boid's speed
    # Slow step! Lookup the "alpha max plus beta min" algorithm
    speed = sqrt(boid.vx*boid.vx + boid.vy*boid.vy)

    # Enforce min and max speeds
    if speed < minspeed:
        boid.vx = (boid.vx/speed)*minspeed
        boid.vy = (boid.vy/speed)*maxspeed
    if speed > maxspeed:
        boid.vx = (boid.vx/speed)*maxspeed
        boid.vy = (boid.vy/speed)*maxspeed

    # Update boid's position
    boid.x = boid.x + boid.vx
    boid.y = boid.y + boid.vy

Fixed Point Arithmetic

Floating point is too slow for animation, so you will be using a fixed point data type and doing all arithmetic in fixed point. This animation example on the Dev Board page does animation using the _Accum data type. To generate a random number in fixed format:

static _Accum Accum_rand, Accum_rand_scaled ;
//fraction from 0 to 1
Accum_rand = (_Accum)(rand() & 0xffff) >> 16 ;
// range from -2 to 2
Accum_rand_scaled = ((_Accum)(rand() & 0xffff) >> 14) - 2 ;
// to print
sprintf(buffer, "%f", (float)Accum_rand_scaled

Frame Rate

Set the TFT frame time using a thread to be faster than 30/second. Since the computation will be the most demanding calculation and depends on the number of boids, arrange the thread to produce a constant frame rate, while allowing as much time as possible for computation. Here is a pseudocode example of constant frame rate.

Hardware connections to PIC32

• Serial: serial default for protothreads (1.3.2) uses pins:
  PPSInput(2, U2RX, RPA1)
PPSOutput(4, RPB10, U2TX)
  Be sure to uncomment #define use_art_serial in the config file.
• TFT: As described on the Big Board page

Program Organization

Here is a suggestion for how to organize your program:

• Protothreads maintains the ISR-driven, millisecond-scale timing as part of the supplied system. Use this for all low-precision timing (can have several milliseconds jitter).
• Main sets up peripherals and protothreads then just schedules tasks, round-robin

  • Initializes TFT display
  • Sets up protothreads and schedules tasks round-robin

• Python Serial Input Thread (see here)

  • Waits for input from Python user interface. The input will specify the value for a parameter (visualRange, protectedRange, centeringfactor, matchingfactor, or avoidfactor).
  • If user input is received, it converts the received value to a fixed-point data type and sets the associated parameter to that value

• Timing thread

  • Increments system time
  • Displays time (in seconds), number of boids, and frame rate on the TFT display, or in Python interface
  • Spawns boids until maximum number of boids is reached

• Animation Thread (See this animation example on the Dev Board page for a place to start)

  • Gets time using PT_GET_TIME()
  • Loops through each boid/predator

    • Erases the boid/predator (draws a black pixel or circle over it)
    • Computes the boid's/predator's updated position and velocity using the algorithm described above
    • Draws the boid/predator at its new position

  • Gets the time again using PT_GET_TIME(), yields for as long as is required for a 30 frames/sec update rate

Weekly checkpoints and lab report

Note that these checkpoints are cumulative. In week 2, for example, you must have also completed all of the requirements from week 1.

Week one checkpoint

By the end of lab section in week one you must have:

• Starting from this animation example on the Dev Board page, get at least one boid flying around the TFT display with the following hardcoded parameters:
  
  turnfactor: 0.2
  visualRange: 20
  protectedRange: 2
  centeringfactor: 0.0005
  avoidfactor: 0.05
  matchingfactor: 0.05
  maxspeed: 3
  minspeed: 2
  topmargin: 50px
  bottommargin: 50px
  leftmargin: 50px
  rightmargin: 50px
  
  
• The boid should have randomized initial position (within margins) and velocity (within min/max speed limits)
• Your boid may be represented as a pixel (drawn using the tft_drawPixel routing) or as a circle (drawn using the tft_drawCircle routine). You can draw a pixel faster than a circle, so you'll be able to create more boids if they're represented as pixels. However, you can create larger boids if they are circles. So, consider starting with your boids as circles so that they are easy to see, and then switching them to pixels.
• Your animation should update at a constant frame rate >=30fps (see this pseudocode)
• The TFT display (or the Python interface) should show the number of boids, the frame rate, and elapsed time in seconds
• Finishing a checkpoint does NOT mean you can leave lab early!

Week two checkpoint

By the end of lab section in week two you must have:

• At least 10 boids flocking. This is enough to show that the algorithm is working, but you do not need to have your code optimized by week two.
• The parameters should be initialized to the following values:
  
  turnfactor: 0.2
  visualRange: 20
  protectedRange: 2
  centeringfactor: 0.0005
  avoidfactor: 0.05
  matchingfactor: 0.05
  maxspeed: 3
  minspeed: 2
  topmargin: 50px
  bottommargin: 50px
  leftmargin: 50px
  rightmargin: 50px
  
  
• The boid should have randomized initial position (within margins) and velocity (within min/max speed limits)
• Your boid may be represented as a pixel (drawn using the tft_drawPixel routing) or as a circle (drawn using the tft_drawCircle routine).
• Your animation should update at a constant frame rate >=30fps (see this pseudocode)
• The TFT display (or the Python interface) should show the number of boids, the frame rate, and elapsed time in seconds
• You should be able to change at least one of these parameters via a Python interface and see the flock behavior change as expected.

Week three assignment

Timing of all functions in this lab, and in every exercise in this course will be handled by interrupt-driven counters, not by software wait-loops. ProtoThreads maintains an ISR driven timer for you. This will be enforced because wait-loops are hard to debug and tend to limit multitasking

Write a ProtoThreads C program which does the following:

• At reset, the program spawns as many boids as it can while maintainting 30fps animation rate. The program will use the following parameters for the flock of boids:
  
  turnfactor: 0.2
  visualRange: 20
  protectedRange: 2
  centeringfactor: 0.0005
  avoidfactor: 0.05
  matchingfactor: 0.05
  maxspeed: 3
  minspeed: 2
  topmargin: 50px
  bottommargin: 50px
  leftmargin: 50px
  rightmargin: 50px
  
  
• The boids should have randomized initial position (within margins) and velocity (within min/max speed limits)
• The boids may be represented as pixels or circles, as long as they are visible
• Your animation should update at a constant frame rate >=30fps (see this pseudocode)
• The TFT display or Python interface should show the number of boids, the frame rate, and elapsed time in seconds
• Through a Python interface (see here), the user may specify new values for visualRange, protectedRange, centeringfactor, matchingfactor, and avoidfactor. The flock will immediately begin behaving according to the new parameters.

Write a Python program which does the following:

• Enables the user to specify values for visualRange, protectedRange, centeringfactor, matchingfactor, and avoidfactor (sliders work well for this, but you may do whatever you'd like)
• I recommend that the flock start with the default parameter values given above, and that your interface enables the selection of values within the following ranges for each parameter

  • protectedRange: [0, 100]
  • visualRange: [0, 200]
  • centeringFactor: [0.0002, 1] (ok to represent as the reciprocal value if that's easier)
  • avoidFactor: [0.01, 1] (ok to represent as repicrocal value if that's easier)
  • matchingFactor: [0.01, 1] (ok to represent as reciprocal value if that's easier)

• See below for an example of what your interface might look like

Python interface for flock control.

ECE 5730 students

In addition to all of the above, ECE 5730 students must also do the following:

• Implement at least one predator, with behavior described in previous parts of this document. Use the following parameter values:
  
  predatorturnfactor: 0.4
  predatorRange: 50
  
  
• Add predatorRange to the list of parameters that can be varied in the user interface.
• An example video of a flock with a predator is shown at the bottom of this page.

Lab report

Your written lab report should include the sections mentioned in the policy page, and:

• A few cool photographs of your flock
• A heavily commented listing of your code

Opportunities to keep going

If you're having fun, there are opportunities to extend these rules to generate additional behaviors. If not for this lab, perhaps as a final project?

• Make a more sophisticated predator. Perhaps it moves toward the center of mass of all boids in its visual range. Or, perhaps it picks a single boid in its visual range and moves toward that boid (that seems like more realistic behavior to me, but who knows). The boids will, of course, avoid the predator.
• Add perching behavior. Draw a background on the TFT (a tree branch, a simple ledge, whatever). If a boid gets near that object, have it pause on it for a certain amount of time, and then take off again.
• Add gravity. Birds tend to move more quickly when diving than when ascending. Incorporate that into your flock.
• Add a moving food source (or sources) that the boids track

Example of working system

In the example below, the flock parameters are changed from the command line. When avoidfactor is increased (at ~7sec), you can see the flock rapidly disperse. By playing with dynamic variations of these parameters, you can make your flock do very interesting things.

And below is a demo video that includes a predator.