EE 476: Laboratory 4

Video Game -- Lunar Lander

You will produce a version of the classic video game Lunar Lander (example). The lander thrust will be controlled by an analog input, and the lander attitude by button pushes. There will be a fuel limit. Display will be on a TV, with sound effects.

You will probably want to review the code examples given in Video Generation with AVR.
Use this example as a basis for your program. Before compiling, under the Project menu, choose Configure... , then in the Compiler tab. Set "Optimize for Speed", reduce the Data Stack size to 100 bytes, and turn off the "char is unsigned" option.

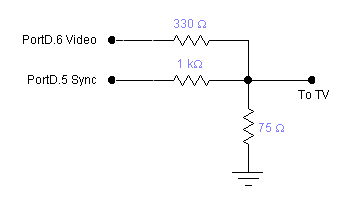
Build the video DAC shown below and connect it to the yellow connector on the TV using clip leads and a RCA phone jack. Make sure the TV is set to video input. Test the TV connection using the example program linked above. The power supplies on the TVs and development boards are NOT interchangable.

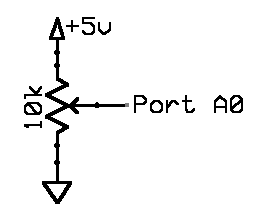
The lander thrust (acceleration) will be controlled by a potentiometer hooked to an A/D input on the MCU. Use the following circuit make a user-variable voltage. I suggest setting Vref to Vcc on the A/D converter. This example shows how to set up the A/D converter.

You are going to be programming in the equations of motion for the lander. Your controls will be attitude and thrust, so we will need to relate acceleration, velocity and position. Remeber that the video coordinate system has x increasing to the right and y increasing downward. If θ is the angle of the lander from the vertical (and measured positive counterclockwise) then the acceleration is:

ax=-thrust*sin(θ) and ay=g-thrust*cos(θ)

Computing the velocity change over a short time (by the Euler method)

vx(t+dt)=vx(t)+ax*dt and vy(t+dt)=vy+ay*dt

Computing the position change over a short time (by the Euler method)

x(t+dt)=x(t)+vx*dt and v(t+dt)=y(t)+vy*dt

The fuel level is

fuel(t+dt)=fuel(t)-thrust(t)*dt

Clearly, v, x and fuel all need initial conditions, which you will set, according the specifications below. It is doubtful that you will have ehough time between frames to do all of the calculations in floating point. I suggest using 16 bit, signed numbers with the binary point set at the byte boundary. I also suggest scaling g and the thrust so that you can make dt=1, thereby avoiding the multiply. There is an example of a bouncing ball with drag done with fixed point numbers.For speed, you will have to make a table of sines and cosines for limited number of angles that the lander can assume.

Examples of student work:

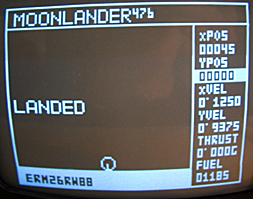:Photo by Eric Mesa, 2005

Gus Lott (2005) hooked the Mega32 video directly to his video capture card and produced this 8 Mbyte wmv file.He and his partner decided that 8-bit fractions caused too much granularity in the controls, so they used 24-bit fractional arithmetic. Basically, a realistic feeling g was around 0x0004-0x0006 so you only had 4 to 6 levels of manipulation around that g value with a thrust. This made it really hard to control. If you turned the dial to far, you were suddenly thrusting at many times the g level. This also produced some weird quantization noise after sin/cos scaling of the thrust. So they cast all of their floating point numbers into longs (24 fractional bits) and overlaid the direct 8 bit analog value of the A/D with the most significant bit left shifted 14 bits in the long. Then max thrust the user can give is 0x003fc000 with a g of 0x00040000 and a pixel at 0x01000000. Their arithmetic was, in reality, only 22 bit, but longs were the easiest way tohandle it in C. The extra precision made for real smooth manipulations, with 256 different thrust levels from 0 to +11g as opposed to approximately 20 thrust levels in the same range.

Write a program in C and assembler for the microcontroller with these specifications:

• At reset, the program should:
  • draw an elementary landscape at the bottom of the TV screen.
  • set the running time clock to zero.
  • start the lander in the upper-left corner of the screen with v_x=10 pixels/sec and v_y=0. You can vary this to make the game more playable, if necessary.
• At each frame, update the acceleration, velocity and position of the lander, and redraw the lander. The drawing of the lander need not be complicated, but must include an indication of the direction of the thruster.
• Lander attitude should be changed by two pushbuttons (clockwise and counterclockwise) with each press changing the attitude, θ, by 15 degrees. Attitude should be limited to +/- 90 degrees.
• The thrust available should be scaled to be about twice g (gravity) and be controlled by a potientiometer attached to the A/D converter.
• The initial fuel should be scaled to allow you to land with very little extra.
• The game ends when you crash or when you land, or if you go off the screen. There should be appropriate loser messages displayed if you crash or go off screen. There should be an winner message displayed if you land.
• Sucessful landing occurs if you reach a level spot on the surface, with very low horizontal velocity and low vertical velocity. Horizontal velocity must be below 0.5 pixel/sec and veritcal velocity less than 2 pixels/sec. These values are open to negotiation.
• There should be no video artifacts (rolling, tearing, flickering) during operation.
• Optionally, you could also compute total remaining fuel and update an fuel indicator and sound a warning if the fuel level falls to 10% of the initial fuel

When you demonstrate the program to a staff member, you should exercise all the lander functions.
You should be able to actually land your craft.

Your written lab report should include:

• The scheme you used to coordinate video and the ADC.
• The details of your integration algorithm.
• An image from the TV (bring your camera).
• A heavily commented listing of your code.