ECE 5760: Laboratory 3

Mandelbrot set visualization.

Introduction.

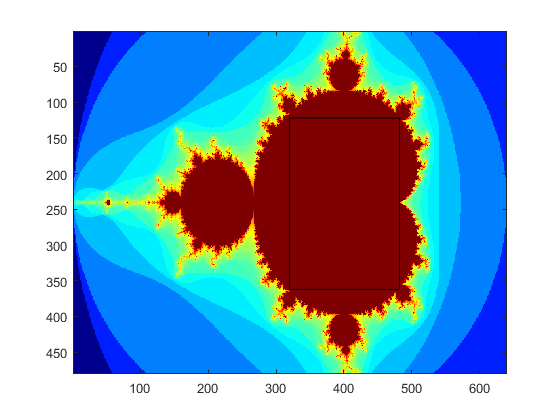
In this assignment you will implement a system to compute and draw the Mandelbrot set, and to zoom in on pieces of the set. A matlab program shows how the computation is done. Note that the numbers are all complex. The image below is from the program output. The x,y axis units on the image are pixels, not natural units. The actual x axis range is [-2,1] and the y axis [-1,1]. The rectangle is the largest rectangle I could fit into the set.
Former TA, Shiva Rajagopal, found a video for Mandelbrot Set made by Cornell students! https://www.youtube.com/watch?v=ES-yKOYaXq0
Lyrics: http://www.jonathancoulton.com/wiki/Mandelbrot_Set/Lyrics

Procedures:

• There may be a HPS to control computation and set parameters.
  Baseline perfromance that you must beat is my best single-processor HPS code.
  Read the University computer page, Mandelbrot example.
• You will use custom bus-master hardware to compute the image. The computation of a 640x480 image is compute intensive, so you are going to want to implement multiple computational units to speed up the process. Spend some time considering load balancing since some regions of the complex plane are much faster to compute than others. Initial testing suggests that you can calculate and display the mandebrot set approximately 30 times faster on FPGA hardware, than on the HPS. The computation must output directly to VGA and not pass results through the HPS.
• For the custom hardware, I suggest using a minimum of 4.23 fixed point notation for interating the quadratic complex number calculation. The number of bits carried will limit the zoom depth. Every bit gives one level of zoom, but you need 10 bits to represent the screen width, so 23 bits gives only 13 zoom levels. The top bit will be the usual 2's comp sign bit. The 4.23 notation means that a single DSP unit can do one multiply. This format give the numbers a dynamic range of +/-7. A matlab program to check the effect of limiting the range shows that the computation works without overflow.

Examples from class:

• 2018 -- video1, video2, video3 ; 20 solvers, 100 MHz.
  Effective arithmetic rate is about 10 billion operations/sec.
  Thanks: Xitang Zhao and Vidya Ramesh
• Skyler Schneider 1, 2, 3, 4
• Venkatesh Santhanagopalan and Rick Wong 1, 2, 3
• Jinda Cui and Jiawei Yang, Full set.;
  Satellite double spiral: x_mid=-0.743 643 900 055; y_mid=0.131 825 890 901; zoom level=3000;
  neural network: range mode: x=(-0.37432239 -0.373655726 ); y=(0.65938433 0.66005100); zoom mode: x_mid=-0.37398906; y_mid=0.65971767; zoom level=3000;
  devil's eye: range mode: x=(-1.87 -1.85); y=(-0.01 0.01); zoom mode: x_mid=-1.86; y_mid=0; zoom level=100;
  alien's egg: range mode: x=(-1.863 -1.85); y=(-0.00153846 0.00153846); zoom mode: x_mid=-1.8615; y_mid=0; zoom level=650;
  lava: range mode: x=(-1.38 -1.36);y=(-0.026 -0.006); zoom mode: x_mid=-1.37; y_mid=-0.016; zoom level=100;
• Sandeep Gangundi and Sion Wang 600x_zoom
  

  image name	x coord	y coord
  flower	[-0.37465401, -0.37332411]	[0.659227668, 0.66020767]
  asymmetric mandelbrot	[0.435396403, 0.451687191]	[0.367981352, 0.380210061]
  pattern	[-0.758,-0.75]	[0.05,0.06]
  spiral	[-0.403, -0.399]	[-0.600, -0.603]

• Mohammad Saifee Dohadwala
  

  name	complex cood x	complex cood y
  SPIRAL	x = [-1.339301 , -1.336371]	y = [-0.060742 , 0.058789]
  INVERTED MANDELBROT	x = [0.385683 , 0.388613]	y = [-0.268013 , -0.266060]
  Spiral 2	x = [0.379813 , 0.381278]	y = [-0.275228 , -0.274251]
  STARFISH	x = [-0.670565, -0.669833]	y = [-0.458300, -0.457812]

Other links

• A student report on implementing a mandelbrot generator on a DE1 board.
• Mark Bowers FPGA-based Mandelbrot generator
• Mandelbrot set
• MIke Field Mandelbrot on FPGA
• Who needs VRAM anyway? Or, calculating Mandelbrot on an FPGA
• Properties of Mandelbrot set
• Optimizations

Assignment

Weekly check points

1. Week 1:
   -- demonstrate a simulation of one complex iterator pipeline. The number of iterations required should match the equivalent matlab point in the complex plane for at least two points.
2. Week 2:
   -- demo more than one complex interator bus-master writing to the VGA bus-slave to show full Mandelbrot Set on the VGA.
   -- demo interactive zooming on the VGA.
3. Week 3: demo full system below

Full System

• You may use HPS for control, but you do not have to.
• You do need the best HPS time for comparision to FPGA solution time.
• The corners of the region being plotted should be displayed either on the VGA screen, or on a serial console.
• You should be able to choose the maximum number of iterations using serial input the HPS, or toggle switches, or however you want to do it.
• Upon pressing KEY3, the system should compute and display the full Mandelbrot set, as shown above.
• The computation must be a bus-master output directly to the VGA bus-slave, and not pass results through the HPS. The VGA graphics interface should run the VGA at 640x480 resolution with at least 8-bit color per pixel. Colors may aid in debugging and certainly look cool. You may want to map color to the number of iterations to divergence, or to the log of that number. A reasonable approximation of the log is to just use the position of the largest non-zero bit in the count (in matlab fix(log2(count)). A modified matlab program and image show the effect of log-compressing the numerical range. The zoomed image (see below) also shows different detail.
• There will be a zoom interface using push buttons, or serial communication to a terminal or a mouse interface. It is sufficient to pick a center coordinate and zoom in/out by a factor of two. When you trigger the zoom calculation, the specified corners should be reassigned to the corners of the display and 640x480 new points in those intervals should be iterated again.
• Part of your grade will depend upon how fast you can render the full 640x480 set and two other regions picked on demo day.
• The elapsed time to draw the screen (in milliseconds) should be shown on the VGA screen.
  
• You will need to show how your solution time for the full set depends on the number of solver pipelines used.

Be prepared to demo your design to your TA in lab.

Your written lab report should include the sections mentioned in the policy page, and :

• A table of times to compute various regions of the Mandelbrot set close to the areas specified in the list.
  • x=[-2 1], y=[-1 1]
  • x=[-0.758,-0.75], y=[0.05,0.06]
  • x=[-1.45, -1.3], y=[-0.07, 0.07]
• A collection of photographs of your favorite regions, and their coordinates. The camera should be good enough to resolve individual pixels.
• A table of your solution time for the full set versus the number of solver pipelines used
  and for FPGA solution versus HPS solution time.
• A detailed dsecription of your Qsys design.
• A heavily commented listing of your Verilog design (for FPGA) and GCC code (for HPS).