Background

  The evolutionary algorithm is a powerful algorithm used to optimize systems to solve a specific function. It has been used with much success in engineering, biology, economics, marketing and social sciences to name just a few fields. The aim of this project is to optimize a neural network consisting of sensory inputs, intermediate neurons, and response (or output) neurons using an evolutionary algorithm for a specified task . A particularly interesting problem to solve in this field is the Tracker task . This task is inspired by the behavior of certain species of ants that lay down pheromone trails from a food site to their nest to aid in the process of collective foraging. 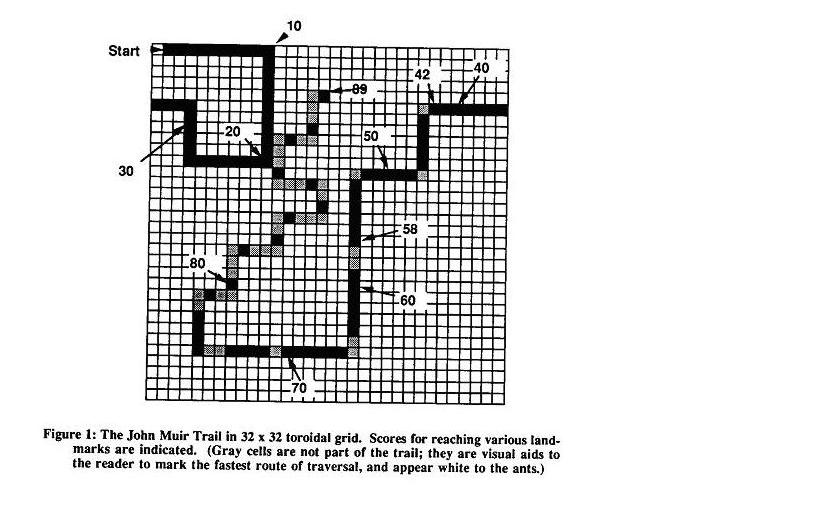The task requires an ant to follow a crooked, broken trail of black cells in a white toroidal grid as shown in Fig. 1 (taken from Jefferson et al.):
this stu

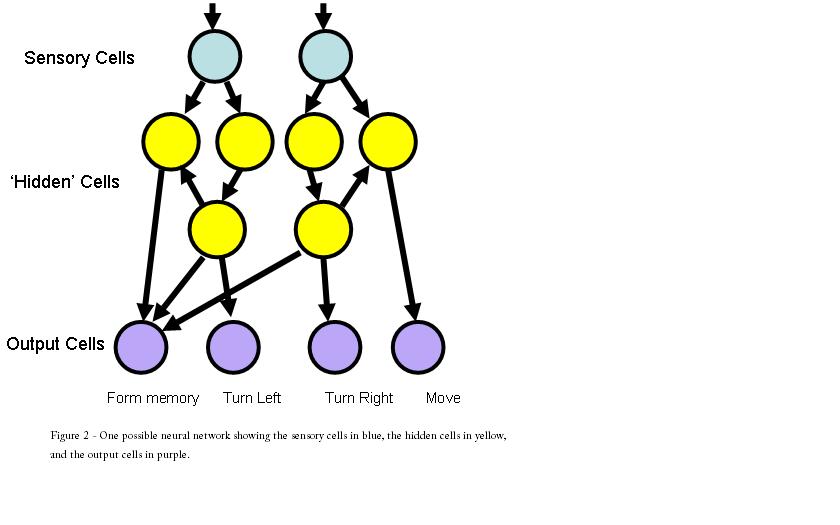
In this study, they evolve a very simple system with 2 input units, 5 hidden units, and 4 effector units (Fig 2).  In my project I propose to set up a very similar system, however with added hidden units that can interact with each other as well as with the input and output units, and add the ability for each cell to store a certain amount of permanent changes during its track.  Once this system is set up, it will be used to answer several interesting questions about both the evolutionary algorithm and the structure of neural networks, such as:

·        How many generations of how large of a population are required for an efficient final result (i.e. how fast is the convergence to an optimal solution).

·        What minimum number of “hidden” cells are required for a minimally effective solution, is there a continued increase in performance with more processing units or is there a maximum after which the addition of more cells yields insignificant benefit?

·        If one considers a ‘time cost’ to creating permanent changes in the processing units, will there still be a benefit over not having this ‘memory’ function?