So the basic components of a digital hourglass would include a display, sensors to detect tilt angle relative to some fixture (like earth ground), a microcontroller, a speaker alarm, and buttons.

As detailed in the hardware section, we used a 256x128 LCD as our display, accelerometers as sensors, and Atmel's ATmega163 as our microcontroller.  Tiny speakers were relatively easy to obtain, and the programming board for the microcontroller has buttons.

Upon programming the ATmega163 MCU, the hourglass and sand would display on the LCD. By moving around the accelerometers, we would be able to change the angle of the hourglass, which should result in real-time motion of the sand.

The accelerometer outputs different voltages when it is moved to various angles. The voltage would go into the analog-to-digital (A/D) converter. The converted voltage would then be decoded into a certain tilt angle be used to determine the positioning of the sand.

• Although it is possible to hardcode a fancy hourglass image into flash, as described on Mike Rankin's website, we opted not to do that simply due to sheer amount of flash needed for a 256x128 image. We chose to draw a primitive hourglass using the FillRect() function (see the software section for more details). We made a dumbbell shape to represent the hourglass:

  

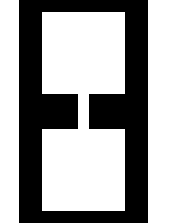
  Hourglass graphics on LCD

• As you can see, the two halves of the hourglass are rectangular boxes.  We chose to do this because it would greatly simplify the shape of the sand in the hourglass (see the software section for more details).  Inside a rectangular box, the sand can take shape of either a triangle, rectangle, trapezoid, or pentagon. We eliminated the pentagon case by limiting the total amount of sand inside the hourglass to be less than half of the size of one of the rectangular boxes.

• The various positions that the sand in the hourglass can be in are as follows:

  

  Possible sand shapes in hourglass

• The output voltage from the accelerometers determine the tilt of the hourglass, which in turn allows the vertices of the quadrilateral to be computed. Although a fill function for a three sided figure was not made, we circumvented the problem easily by using the function that fills a quadrilateral; a one-pixel line would be added to the triangle.
• As seen above, all the sand positions are basically quadrilaterals. We developed an algorithm for generating quadrilaterals, with only one slanted edge.
• We simulated the falling of sand by just drawing a straight line. As the sand falls from one side to the other, the sand on the top half of the hourglass should decrease while the sand on the bottom half of the hourglass should increase. We increased and decreased the sand by changing the coordinates of the quadrilateral drawn.