Cornell University
Electrical Engineering 476
Fixed Point DSP functions
in Codevision C and assembler

Introduction

This page concentrates on DSP applicaitons of 8:8 fixed point in which there are 8 bits of integer and 8 bits of fraction stored for each number. The emphasis of these implementations is on speed, but accuracy considerations are addressed in the section on 2nd order Butterworth filters.

This page has the following sections:

One of the most demanding applications for fast arithmetic is digital flitering. Atmel application note AVR201 shows how to use the hardware multiplier to make a multiply-and-accumulate operation (MAC). The MAC is the basis for computing the sum of terms for any digital filter, such as the "Direct Form II Transposed" implementation of a difference equation shown below (from the Matlab filter description). 

    a(1)*y(n) = b(1)*x(n) + b(2)*x(n-1) + ... + b(nb+1)*x(n-nb)
                          - a(2)*y(n-1) - ... - a(na+1)*y(n-na)

The y(n) term is the current filter output and x(n) is the current filter input. The a's and b's are constant coefficients, determined by some design process, such as the Matlab butter routine. Usually, a(1) is set to one, but as we shall see below, setting a(1) to a power of two may increase filter accuracy, at the cost of slightly increased execution time. The y(n-x) and x(n-x) are past outputs and inputs respectively. You can use the Matlab filter design tools to determine the a's and b's. There are also various web-applets around which help design coefficients:

This page is summarized in an article I wrote for Circuit Cellar magazine (manuscript).

First order IIR lowpass Filter for 8:8

When speed of execution, rather than filter performance, is most important, a crude 1-pole, step-invariant, lowpass filter can execute in about 69 cycles. The difference equation is simplified to have just one multiply:
y(n+1) = y(n)*alpha + input*(1-alpha)
or
y(n+1) = (y(n)-input)*alpha + input
where alpha = exp(- π * (normalized cutoff freq)).
You can probably use this filter for normalized cutoff frequencies in the range of 0.01 to 0.4 with reasonable accuracy.

Second order IIR Filters for 8:8

A test code (unoptimized, but easy to understand) implements an efficient MAC operation and then uses it to produce a second order IIR filter. Each sample takes about 400 cycles to filter.

The optimized 2nd order IIR code reduces the time/sample to 182 cycles. It would not be reasonable to use this fixed-point algorithm with normalized cutoff frequency below about 0.10 because of the lack of relative precision in the b coefficients. With a normalized cutoff frequency=0.25, the impulse response is accurate to within 1% of peak response. With a normalized cutoff frequency=0.10, the impulse response is accurate within 5% of peak response. If you need a cutoff lower than 0.10, consider changing your hardware sample rate or averaging together pairs of samples to half the effective sample rate.

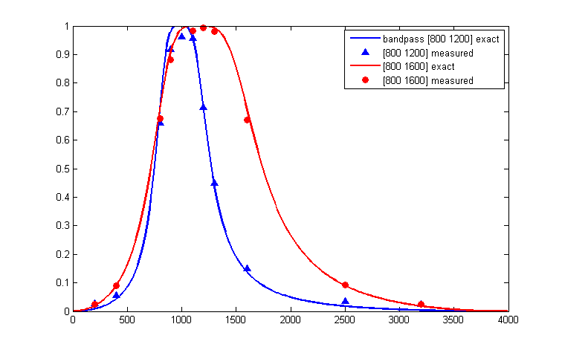
Second order Butterworth IIR Filters for 8:8

If you use a Butterworth approximation for lowpass (maximally flat IIR filter) then you can simplify the general IIR filter further to only three MAC operations. Since b(1)=b(3)=0.5*b(2), the three multiplies on the first line below can be combined into one multiply by sum of inputs, with one input shifted left. 

b(1)*x(n)+b(2)*x(n-1)+b(3)*x(n-2) = 
b(1)*x(n)+2*b(1)*x(n-1)+b(1)*x(n-2) =
b(1)* (x(n)+(x(n-1)<<1)+x(n-2))
While a Butterworth high pass design yields b(1)=b(3)=-0.5*b(2), 
b(1)*x(n)+b(2)*x(n-1)+b(3)*x(n-2) = 
b(1)*x(n)-2*b(1)*x(n-1)+b(1)*x(n-2) =
b(1)* (x(n)-(x(n-1)<<1)+x(n-2))
And a Butterworth bandpass pass design yields b(1)=-b(3) and b(2)=0, 
b(1)*x(n)+b(2)*x(n-1)+b(3)*x(n-2) = 
b(1)*x(n)+0*b(1)*x(n-1)-b(1)*x(n-2) =
b(1)* (x(n)-x(n-2))

Since adding and shifting are much faster than multiplying ,we get a speedup. The lowpass and highpass Butterworth filters execute in 148 cycles, compared to 182 cycles for the general second order IIR filter above. The bandpass takes 140 cycles. All three second order filters are in one test program.

Accuracy of fixed point filters is always a concern. This program allows you to get the amplitude response of a 2-pole filter. Some results are shown below. Notice that as the bandwitdh gets narrower, the accuracy decreases. This is because the b(n) coefficients become smaller and roundoff/truncation error dominates. Actual plots were made with a matlab program which uses the output of the C program. We can minimize truncation errors by scaling the filter coefficients and the filter code. As an example, if we set a(1)=16, and multiply all of the other coefficients by 16, then the value of the output does not change, but 4 more bits are available to store the scaled filter coefficients. An example program shows how to do this. The filter coefficients are multiplied by 16 when they are defined in main. The filter routine is modified to include a divide-by-16 in the following form:

asr  r31  ; 16-bit divide by 16 
ror  r30
asr  r31
ror  r30
asr  r31
ror  r30 
asr  r31
ror  r30
The filter now computes 16*y(n), which is divided by 16 before the filter function returns. The cost in time is 8 cycles. You can scale by any number of bits up to 15, but remember that the integer dynamic range of the inputs will decrease as you scale to more bits. Any of the filter routines can be modified by this simple inclusion of a divide. The error in the following two plots would decrease to less than 1% for a filter which is scaled by 16. This Matlab program allows you to simulate the effect of coefficient truncation on filter response.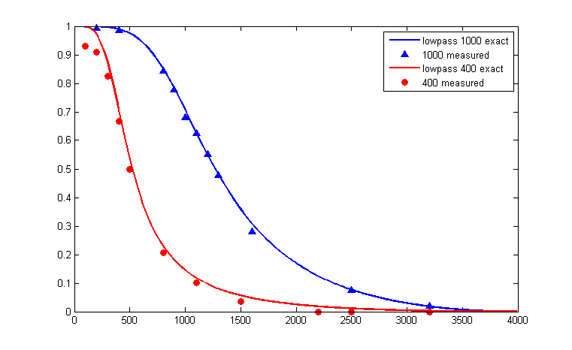

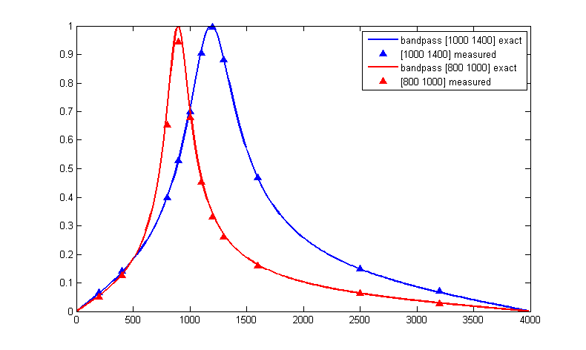
Fourth order Butterworth Bandpass IIR Filter for 8:8

A 4th order Butterworth bandpass filter (2 poles on lower side, 2 on upper side) can be done in 5 multiplies since b(1)=b(5)=-0.5*b(3) and b(2)=b(4)=0. The test program shows that the 4th order routine executes in about 228 cycles. Impulse response accuracy is within 2% after 10 samples with cutoffs of [0.25 0.35]. As the bandwidth of the filter gets smaller, the b coefficients get smaller also and roundoff errors get worse. Various tools exist to choose filter coefficients, for example the Matlab command [b,a]=butter(2,[Flow,Fhigh]) will generate the coefficients for this bandpass filter.

This program allows you to get the amplitude response of a 4-pole filter. Some results are show below. Notice that as the bandwidth gets narrower, the accuracy decreases. Scaling the coefficients as explained in the section above can help accuracy considerably.

Karplus-Strong Algorithm and digital waveguides

The Karplus-Strong Algorithm (KSA) for plucked string synthesis is a special case of the digital waveguide technique for musical instrument synthesis. The KSA is particularly well suited for implementation on a microcontroller, and was originally programmed on an Intel 8080! The simplest version hardly needs fixed point arithmetic, but better approximations do require some more sophisticated digital filters. The basic algorithm fills a circular buffer (delay line) with white noise, then lowpass filters the shifted output of the buffer and adds it back into itself. The length of the buffer (and the sample rate) determine the fundamental of the simulated string. The type of lowpass filter in the feedback determines the timber. Prefiltering the white noise before loading the buffer changes the pluck transient timber. A final project from 2007 used the KSA to make a playable air guitar (video 23MB mp4 ). A matlab program to generate a plucked string is here. A version with some lowpass filtering of the initial noise distribution produces a softer pluck. Changing one plus to a minus makes a brassy percussion sound with a duration determined by the length of the delay line. More information can be found in many articles, but these three are very readable:

A generalization of the digital waveguide technique involves multiple waveguides, each with a bandpass filter. This is refered to as banded waveguides and is explained in papers by Essl, et.al including:

The aim of banded waveguide programs is simulate spectrally complicated drum, bar (e.g. vibraphone), or multiple-string instruments. A matlab program to compute one banded waveguide is here. A banded waveguide with several diferent buffer lengths, and hence natural frequencies, (but no interaction between modes) is here. Modifying the program for additive mode interaction changes the sound somewhat. Parameters to control include:

Please note that many of these techniques are patented by Stanford University and licensed to Yamaha and others.

A review of musical synthesis techniques from 2006 is Discrete-time modelling of musical instruments, by Valimaki V, Pakarinen J, Erkut C, Karjalainen M, in REPORTS ON PROGRESS IN PHYSICS 69 (1): 1-78 JAN 2006

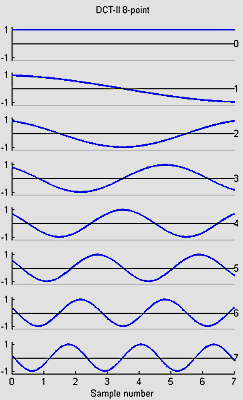
Discrete Cosine Transform (DCT) for 8:8

The DCT is a variant of the FFT which is used in image, sound, speech, and video processing and compression.
I wrote 8,16 and 32-point versions:

The basis functions for the 8, 16 and 32-point versions shown below are similar to the FFT, but capture gradients with fewer coefficients. For example, the first basis function (not the zeroth) in all images encodes an almost linear gradient, something which takes a sum of several basis functions of a Fourier series. The Matlab program to generate the plots is here.

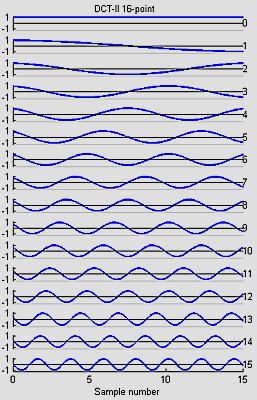
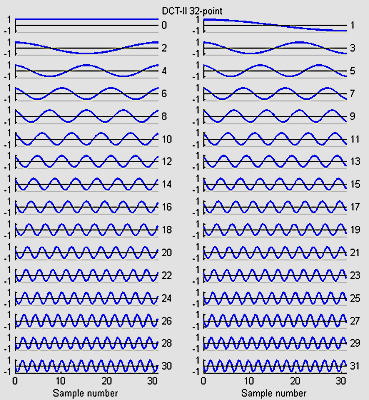
Fast Fourier Transform (FFT) for 8:8

I adapted the int_fft.c program from this webpage.

There are many uses for a FFT including filtering, convolution, and pattern matching. Some applets.

Fast Walsh Transform (FWT) for 8:8

I wrote a FWT which converts a time sequence to coeffieients of the orthogonal Walsh-function basis. An example of the first 16 basis functions from Jacoby and 64 basis functions from Pichler is shown below. Odd functions are called sal, analogous to sine, while even functions are called cal. The following functions are in arranged in sequency order. Sequency is defined as the number of zero crossings, and is anaogous to arranging sines in frequency order.

  1. The first algorithm I used was from Manz. It was first converted to Matlab code, then to C. The Matlab code compares the FFT and FWT outputs as spectrograms, then takes the maximum of each time sliced transform and compares these spectrograms. Examples are spectrogrms for a chirped sine, chirped square wave, a woodthrush, and a fragment of human speech. FFT power spectrum is the top row, FWT sequency spectrum (sum of absolute value of sal and cal coefficients) is the bottom row. Both transforms are 128 points. The right column of images has been formed from the left by finding the maximum intensity coefficient of each spectrogram time slice. Note that the max component of the FFT and FWT match fairly well. Jacoby has useful information on using FWT. Ritter has a good biblography. 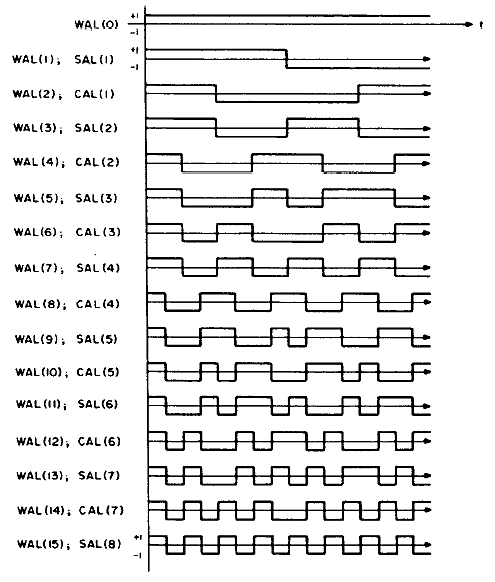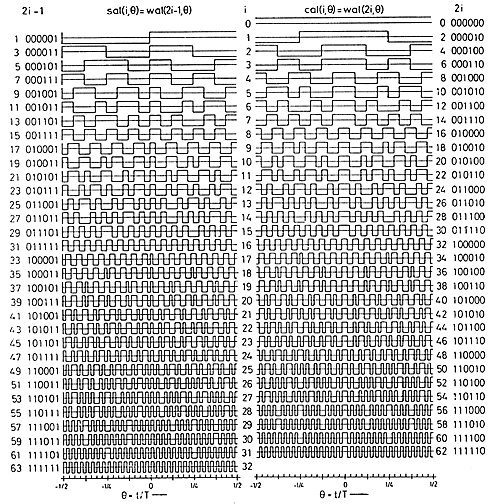This C program executes a 16 point transform in 3600 cycles (with optimization set to speed). Note that the output of the FWTfix routine is not in sequency order (it is actually in dyadic order). Order is not important for some applications. Run the FWTreorder routine to make a sequency order, but note that you must use the correct length reorder array. The reorder routine takes about 1800 cycles to order 16 points. Removing the normalization from the inner loop drops the execution time to 2700 cycles, but can cause overflow if longer transform lengths are used or if the average data approaches full scale for 8:8 numbers.
  2. The second algorithm I used was from from Hugh Larson, An algorithm to compute the sequency-ordered FWT, IEEE Transactions on Acoustics, Speech and Signals, Aug 1976 page 335. This program version is hard-coded for 16-points, is unnormalized, and executes in 1100 cycles. Including the conversion to sequency order, it is over 4 times faster than the general version above.

This C program attempts to light up leds corresponding to which sequency bands have the most energy. The program takes a 16 point FWT, throws away the DC component, adds the absolute value of the sal and cal components, then lights an LED if the component is the maximum and above a threshold. The main loop is not very optimal.

Copyright Cornell 2007