ECE 5760: Laboratory 3

Multiprocessor Drum Synthesis.

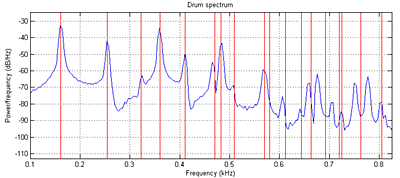
For this exercise, you will simulate the 2D wave equation on a square mesh in realtime to produce drum-like sounds.
This year we will add a nonlinear effect related to the intantaneous tension in the mesh.

Read Study Notes on Numerical Solutions of the Wave Equation with the Finite Difference Method. The main result you will need to simulate is equation 2.18. A matlab program gives a sequential version of the algorithm and plots the Fourier modes of the drum. Another version is tuned to middle C (261 Hz). You can see in the figure below that the simulated sound spectrum (blue) matches the theoretical drum modes (red) up to about mode 8 or 9 (see Physical modeling with a 2D waveguide mesh for details) . The theoretical square drum mode frequencies follow the ratio sequence:
sqrt(m+n) where m,n=1,2,3,...
Where the first term (sqrt(2)) corresponds to the fundamental mode of the drum.
The first few modes are sqrt(2), sqrt(5), 2*sqrt(2), sqrt(10), sqrt(13), sqrt(17), sqrt3*sqrt(2).

Modifying the boundary conditions, damping, wave speed, drum size, and distrubution of input energy can modifiy the sound of the simulation from drum-like, to chime-like, to gong-like or bell-like. You can modify the program further to include frequency-dependent damping and other effects. This version simluates a long, thin bar struck at one end.

Adding tension modulation allows pitch bending observed in a real drum after a large amplitude input. The large amplitude means that the membrane is stretched more, and therefore the speed of propagation (and therefore pitch) is increased. This matlab code produces an exagerated pitch effect with initial high amplitude.

You will probably want to read

• IMPLEMENTATION OF FINITE DIFFERENCE SCHEMES FOR THE WAVE EQUATION ON FPGA
• PARALLEL IMPLEMENTATION OF FINITE DIFFERENCE SCHEMES FOR THE PLATE EQUATION ON A FPGA-BASED MULTI-PROCESSOR ARRAY
• Time Domain Numerical Simulation for Transient Wave Equations on Reconfigurable Coprocessor Platform
• Design Methodology for Real-Time FPGA-Based Sound Synthesis

for ideas on parallelization. Also read documentation on incrementail compilation. Some compile times may be very long.

You may want to read the Evans and Sutherland HDL guide, chapter 9, for info on using generate statement.

The hardware audio interface is a Wolfson WM8731 codec which is controlled by an I2C interface. I have simplified the drivers somewhat. The cleanest version is in this project zip. The context for the drivers is explained in the DSP page, example 1. The audio codec produces (and outputs) 16-bit 2's complement numbers. The 16-bit numbers should be considered as fractional values in the range +1 to -1 volt. This example (courtesy of Scott McKenzie and Miles Pedrone) outputs a square wave from the audio port. The first example on the DE2 hardware page shows how to hook up a DDS example.

Student examples running on FPGA:

• 2008: Matt Meister and Cathy Chen wav file.
• 2008: Parker Evans and Jordan Crittenden wav1, wav2
• 2010: Skyler Schneider wav base drum
  with n = 16 ,rho = 0.05, eta = 2e-4, alpha = 0.1, boundaryGain = 0.0, node hit = (8, 8), node probed = (8, 8)
• 2010: Peter Kung and Jsoon Kim, rho bit shifted = 6, 8, 10, 11, 14
• 2010: Kerran Flanigan, Tom Gowing, Jeff Yates, chickencan, glasshit, littlebongo, minibell
• 2011: Jinda Cui and Jiawei Yang, drum, bass drum, bowl
• 2011: Weiqing Li and Luke Ackerman, low, high
• 2011: João Diogo Falcão, growing grid, old MacDonald.
  The growing grid starts at 7*34*4=952 nodes, (#columns*#lines*symmetry), and ends at 254*34*4=34544 nodes. This is with Rho=0.5 and Eta=0.000244.
• 2014 Saisrinivasan Mohankumar, Ackerley Tng, Ankur Thakkar, eta = 0.0002, rho = 0.5 and 0.25, boundary gain =0, Number of nodes = 89x257x2 ( rows x colums x symmetry) = 45746 nodes.
  Lower, Higher
• Christine Soong, Mary had a little lamb

1. Build a realtime drum simulator which produces sound from the audio interface.
2. The simulator should solve the 2d wave equation to produce selectable effects.
   A minimum of three buttons on the DE2 should produce different timbers.
   Timber can be set by boundary condition, eta, rho, tension modulation, or number of nodes.
   At least one timber must include audible nonlinear tension modulation effects.
3. Part of your grade will be determined by how many nodes you can simulate in realtime at an audio sample rate of 44KHz.
   There should be exactly one computational update of all the drum nodes for each audio sample.
   Each sample that you calculate must be output to the audio codec.
   Each node simulated will require around 10 additions/multiplications. You may be able to use clever shifting schemes to avoid multiplys. Thus the computation rate will be about
   10*(number of wave equation nodes)*(audio sample frequency) .
   For a minimal 10x10 grid at 44 kHz, you will need 1000x44000=44x106 operations/second. For a more accurate 20x20 grid you will need ~200x106 operations/sec. Clearly some parallel processing will be necessary.
4. You can use fine-grained parallelism or course-grained multiprocessors. You can use NiosII or Pancake or not, as you wish.
5. Record the audio output back into matlab to show that your simulation matches drum modes (under the correct boundary conditions, etc).

Be prepared to demo your design to your TA in lab.

Your written lab report should include the sections mentioned in the policy page, and :

• Mathematical considerations (what you actually implemented)
• Your parallelization scheme
• A plot of the power spectrum of your drum sounds for each different timber
• A heavily commented listing of your Verilog design and GCC code (if you use NiosII) or Syrup code (if you use Pancake)..