          |

High Level Design
Rationale and sources
We wanted to make the game as real as possible, and decided to draw the ball to the exact proportional specifications, with respect to the table and actual pockets. A main source was the actual pool table measuring 88 x 44 inches, having 2.2 inch diameter balls, corner pockets that were 6 inches from one end to another and side pockets that were 5.5 inches in width. To illustrate our "Pool in a box" concept, we decided to make the whole system run on batteries, whereby the Microcontroller (Mega 32) would run on a 9V battery voltage regulated to 5V, the LCD display would run on two 9V batteries connected directly to the LCD display via a simple switch, accelerometers attached to a linear potentiometer that could be easily stuck to a pool cue, and finally a rotary potentiometer attached to a small representation of our pool table.
We wanted our pool game to be completely portable, and the best way to do this was to use a large graphical LCD display instead of a TV screen. We chose the Seiko G321D LCD panel, partly because it was large (320x200 pixels) and also the fact that groups from previous years had used the panel before. The graphical system did not require a certain sync timing (unlike the TV) but rather two ports sending commands and data to be written and read. The ability to operate with less constraints on timing was important as we have a complicated mathematical system to loop through.
Using my personal cue, we attached linear potentiometers, rotary potentiometers and accelerometers to make sure that the structure was firm and would not fall easily. Since our design is meant to be portable, all the items are to be easily detachable and re-attachable. We decided to place all the items in a cardboard box (hence our name "Pool in a box"
We searched for many websites for physics on pool and found the following explaining about the intricacies of pool.
1. http://www.jimloy.com/billiard/phys.htm 2. http://aci.mta.ca/TheUmbrella/Physics/P3401/Investigations/BilliardCollREC.html
Background Math and Physics
Moving not 1, but a total of 16 balls around on a table require rather complicated physics. In fact, certain simplifications have already been made. For example, we assume that the cuestick always strikes the centre of the cueball, and when calculating velocity, we neglect the effect of ballspin. From what we observe on the LCD, such simplifications do not affect the results too much.
Where ball physics is concerned, a few scenarios have to be considered.
1) Impact with the cuestick
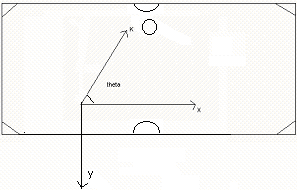
Fig 1. Impact with the cuestick
Upon impact with the cueball, the acceleration of the cue is measured using the accelerometer hooked up to the ADC converter. Using the formula
v = u + at
where u=0 for a stationary cue ball, we determined that the initial velocity of the cueball is a*dt, where dt is the small period of time that the cuestick is in contact with the cueball. From various resources such as online websites, as well as through trial and error, we assigned 0.01s to the value of dt.
On impact, we too need to determine the direction the cueball would be traveling in. For this purpose, we need to define an angle theta, which, like the math you learned in high school increases from 0 to 2 pi anticlockwise. 0 is defined as the angle when the thrust is toward the right direction and pi when the thrust is toward the left.
Since all positions and velocities are ultimately referenced from a common x,y coordinate axes, we need to break down v into its component vx and vy. Hence,
vx = v * cos theta
vy = -v * sin theta
vy has a minus sign in front of it because the y axis points downwards, not upwards.
2) Slowing down
Like all other things, pool balls ultimately slow down due to a mysterious force known as friction with the table top. For this, we simply incorporate a drag force into our calculation of velocity using
v = v - drag * v
3) Collision with the wall
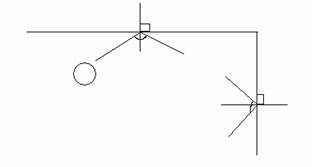
Fig 2. Collision with the wall
When a ball hits the the rail, called a rail or a bank shot, the angle of incidence is the same as the angle of reflection. Hence,
Upper and lower rail hit:
vx = vx
vy = -vy
theta = 2*pi - theta
Side rails hit:
vx = -vx
vy = vy
theta = pi – theta
4) Collision between 2 balls
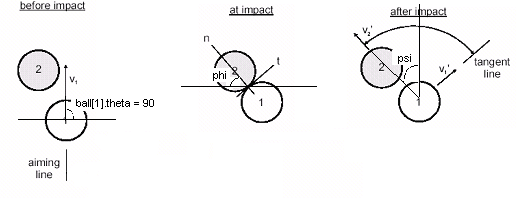
Fig 3. Collision between two balls
Here, to illustrate, we use a simple case of ball[1].theta = 90o, ie the aiming line is in the direction of the negative y-axis. The impact line is a line drawn between the center of the 2 balls when they come into contact. To calculate the angle between the impact line and the horizontal x-axis, we have
phi = tan-1 [ (-ball[1].y - ball[2].y) / (ball[1].x - ball[2].x) ]
On impact, the object ball, ball 2 moves in the direction of n (direction of the impact line).
ball[2].theta = PI + phi
Ball 1 moves in the direction of t, perpendicular to the direction of motion of ball 2. Hence,
ball[1].theta= PI/2.0 + phi
To determine the angle between the impact line and the original aiming line (cut angle), we have
psi= ball[2].theta - ball[1].original_theta
According to the law of conservation of momentum,
v’2n = v1 * cos psi
v’1t = v1 * sin psi
Logical Structure
The structure of the program consists of the game, graphical LCD and accelerometers as well as potentiometers and push buttons.
The game
We have the game system containing 10 different states and conditions to simulate events such as the changing of the player, ball entering the pockets, etc. This handles the main bulk of the game, especially changing the variables using calculations that employ physics and mathematics. This is displayed to our graphical LCD.
Graphics
The microcontroller is to send commands to the LCD panel to instruct
The system can also read data from the LCD and see what pixels are there presently before overwriting it. Finally, the controls are by two potentiometers, two accelerometers and different pushbuttons as shown in the picture below.

Fig 4. Linear potentiometer, rotary potentiometer and accelerometer used
We wanted our pool game to be completely portable, and the best way to do this was to use a graphical LCD display instead of a TV screen. We chose the Seiko G321D LCD panel, partly because it was large (320x200 pixels) and also the fact that groups from previous years had used the panel before. The graphical system does not require a certain sync timing (unlike the TV), and thus we have less of a worry of code fitting in within a certain amount of space.

Fig 5. LCD screen showing the game, pushbuttons on the side, and switch to turn on/off
The pool table on the screen is created to be similar to one that is in real life, and the pool table takes up 280x140 pixels, corresponding to 88"x44" on a real pool table. Also, the pool balls were measured to be 2.2" in diameter, so we allocated 7 pixels in diameter for each ball. This was actually the determining factor for the rest of the items, as we were only able to draw numbers recognizably on balls that were at least 7x7 pixels. The different lines and pockets were drawn pixel by pixel, using excel to help us visualize the actual result.
Fig 6. The different balls used, actual 7x7 pixel size is shown
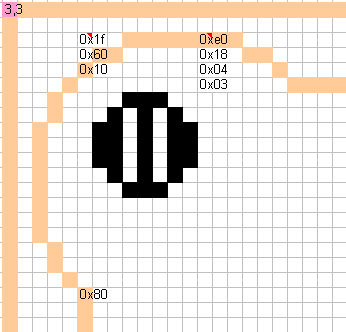
Fig 7. Size of side pocket drawn pixel by pixel
Control
The control of the pool game was mainly through the different accelerometers, linear and rotary potentiometers, accelerometers and a set of push-buttons. The accelerometer lets us know the amount of thrust given by the user, the linear potentiometer shows the actual cuestick on the screen moving, and determines when the cueball is touched, and the rotary potentiometer is used to know the angle with which we actually hit the cueball.
Different buttons on the box allow us to move the balls around during the training phase, so we can choose where to place the ball and try different angles of playing the game. Also, when the cueball enters the hole accidentally or if the player hits an opponent's balls first instead of his own balls, a scratch is called the other player can play the white ball anywhere on the table. The up/down/left/right/next and OK buttons allow all these functions to be carried out.
Hardware/software tradeoffs
Both hardware and software are essential to our game, and our LCD screen needed time to display the images or it would flicker uncontrollably. This meant that our program had to be fast enough to ensure that the flickering would be kept to a minimum. Also, we wanted to get accurate readings for the acceleration, but when we used a 40g accelerometer, the resolution was very low, and when we used the 2g accelerometer, giving more than 2g of force would result in inaccurate readings. Finally, we decided on using the 10g accelerometer as it would have the most resolution for the range of accelerations we needed.
Also, we wanted to take in values using interrupts from the ADC inputs, but our program only ran at 100ms intervals, thus updating values too fast (before entering the program loop). Thus we had to slow down the system to account for such tradeoffs.
For software tradeoffs, we initially wanted the system to be very accurate, and coded the program using floating point calculations. This however was found to be extremely slow and costly in CPU time. We had to change almost everything to fixed point calculation, and this made the whole system much faster. We could not draw too many graphics, as it would take a long time to draw each set of pixels. Also, for drawing a new pixel, the pixel line had to be read, then the new pixel added in, and written back to it again. This slowed down the time allowed for drawing new items.
Design Relations
Our project does not require any specific standards, except that we are not to jab anyone with our cuestick or fight in the lab with it.
Existing Patents
A million and one online pool games can be found readily just by a simple Google search. There are even various leagues and tournaments for those wanting to give their virtual "mouse-clicking" pool skills a challenge. Certainly, in terms of graphics, our "Pool In a Box" is no match for these professional designs. After all, none of them are black and white, and some of them even incorporate 3-D graphics. However, the fact is also that none of them interacts with the user via a real cuestick.
The only exception is the "Automatic Pool Trainer", a project at IMM/KOM, Aalborg University in Denmark. Even then, this design requires a real pool table as well, as it doesn't use an LCD screen for simulated graphical output. More info of this project can be found from The Automatic PoolTrainer Homepage. From a certain perspective, this project definitely feels more real than ours, since it is the actual ball that moves on the actual table. However, portability is a feature that we retain a strong advantage in. "Pool In a Box" means exactly that.
Moreover, as far as we know, it seems that the "Automatic Pool Trainer" has not filed for a patent. Substantial searches have also been conducted for patents of pool games very much like ours, and none has been found thus far.