Introduction
For our final project, we created a spy robot: a robot that uses remote radar sensing to detect intruders. The physical system consisted of the servo setup we had from lab 4, a time-of-flight distance sensor (discussed in depth below), and the PIC32 microcontroller. The distance sensor was affixed to the servo setup and the microcontroller controlled the servos so the assembly could pan back and forth to get distance readings over a set range of angles. Then, this data was stored and sent to the python backend via serial communication to plot the data as a radar map. The data was sent after every full pan so the radar was updating to reflect the environment it was sensing in real time. Thus, the user could view this radar map remotely and detect if there were any intruders based on a change in the radar map.
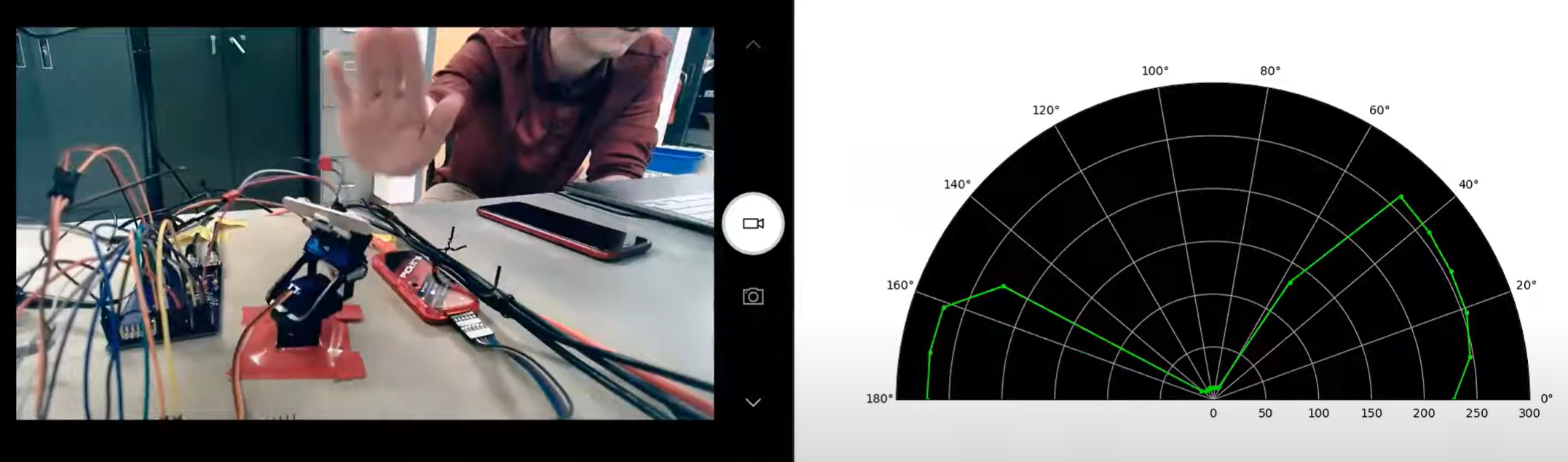
The motivation for the project was to create an embedded solution to a real-world problem: use the PIC to build a real-time remote surveillance system for users to monitor a room. As IoT systems have gained popularity, so has the desire to have surveillance systems that can be remotely accessed. This project explores the implementation of a basic level of this type of system.